(图文)二分查找,查指定值、小于或等于k的最大值,大于或等于k的最大值
我们经常会用到二分查找
二分查找应该很多人都会写了,今天要写一个用二分查找找到小于k的最大值的时候看了很久不懂他设计的思路,后来想通了,记录一下。
所以这篇主要是讲 用二分查找找到小于k的最大值和大于k的最大值。
二分查找查找指定值
这个挺简单的,直接上代码吧
//获取值是k的位置,找不到则返回-1
public static int getK(int[] a, int k){
if(a.length == 0){
return -1;
}
int l = 0;
int r = a.length - 1;
//注意这里的判断条件,是必须允许 l = r 的情况存在的
//因为可能会出现刚好到最后左边指针到右边指针只有1个元素,而且这个元素恰恰就是我们想找的k
while (l <= r){
int mid = (l + r) / 2;
//如果mid元素已经是k了,那么直接返回
if (a[mid] == k){
return mid;
//查找左边的
}else if(a[mid] > k) {
r = mid - 1;
//查找右边的
}else {
l = mid + 1;
}
}
//如果没有找到指定的值,那么直接返回-1
return -1;
}
用二分查找找到小于或者等于k的最大值
思路:如果mid元素是小于或等于k,往右找,如果大于k,往左边找,直到找到一个值,最接近与k的。
看代码中标注了 处地方,下面解释为什么如此设计
//获取值<=k的最大值
public static int uperK(int[] a, int k){
int l = 0;
int r = a.length - 1;
//标注1: 这里是l<r,
while(l < r){
//标注2: 这样的操作是为了取高位
int mid = (l + r + 1) / 2;
if(a[mid] <= k) { //标注3:因为a[mid]<=k,所以a[mid]可能=k,所以mid坐标也满足条件,l = mid而不是mid+1;
l = mid;
}else{
r= mid - 1; //这是a[mid] > k的时候。
}
}
//标注4: 因为此时求得到的是最接近于目标值k的数,
// 如果最小值都大于k的话,那么就没有办法得到了,所以就进行一个判断
if(a[l] > k) return -1;
//标注5: 其实这里无论返回 a[l] 还是a[r]都行,循环的退出时间是l == r 的时候
return a[l];
}
-
标注1解释:
因为我们的目的是“通过缩小范围,得到当l = r的时候,l 标记的值”的情况,所以直到 l< r条件被打破的时候的l就是我们要求的值。这跟上一道问题“查找指定值”是不一样的 -
标注2解释:
标注2: 这样的操作是为了让 mid 标志 取高位, 才能让循环顺序跳出来,举个死循环的例子
注意这个例子采取的是mid = (l + r) / 2 取低位的情况,为了展示死循环的形成过程,我们原题的做法是取高位的
数据: int[] num = {1,2,3,4,5,6,7,8,9}, 查找小于或者等于8的最小值。
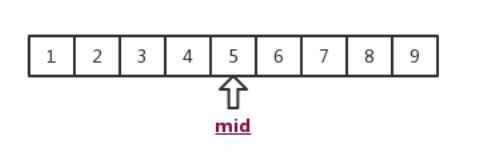
如上图,此时左坐标是0, 右是8, 那么
mid = (0 + 8) / 2 = 4,num[mid] = num[4] <= k, ,向右找结果,所以有 l = mid,开始下一个循环。
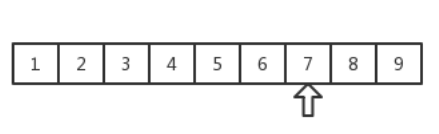
此时的mid = 6, num[6] = 7;
num[mid] <= k, 向右找 l = 6
下一步:
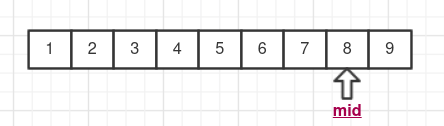
可以得到 l = 6, r = 8, mid = (6+8) / 2 = 7,a[7] = 8 <= k,那么有l = mid = 7, r = 8,
推到得到mid = 7, 问题来了上一步的时候mid已经是7了,结果会使得mid一直是7,一直循环下去。
所以如果我们求的是二分法求小于或者等于k的最大值的话,我们mid 必须取得中值的上界,
- 标注3解释:
因为a[mid]<=k,所以a[mid]可能=k,所以mid坐标也满足条件,l = mid而不是mid+1; - 标注4解释:
如果最小值都大于k的话,那么就没有办法得到了,所以就进行一个判断
最典型的例子是:
{1,2,3,4,5,6,7,8} ,然后k是0的时候, 这样得到的结果只能是数组中最接近与k的数,但是如果他还是大于k
你们可以算一下上面这个例子,到最后num[l] 是1, 永远都大于0, 那么得返回取不到值,所以return -1; - 标注5解释:
其实这里无论返回 a[l] 还是a[r]都行,循环的退出时间是l == r 的时候
二分查找大于或等于k的最小值
直接上代码了,想必大家都清楚了,看了上面问题2的解释
public static int downK(List list, int key){
while (low < high) {
//这里进行的是取低位, 也是为了使得循环可以正确退出,防止死循环
int mid = (low + high)/2;
if (a[mid] < key) {
low = mid +1;
} else { //a[mid] >= key
high = mid; //因为mid也满足情况
}
}
//这里进行检查的原因参考上面的标注
if (a[high] >= key) {
return high;
} else {
return -1;
}
}


