01矩阵系列(计数/最大查询)

51Nod 1291

题意：600*600的01矩阵，统计宽i高j的全1矩阵的个数。

题解：枚举矩阵的下边界，对于每个下边界，统计所有宽极大的矩形的答案（高度可以用差分）。O(nm)的复杂度统计完之后，我们已知所有高度的宽极大的答案，列一下式子发现两次前缀和就是最后答案。

#include<bits/stdc++.h>
using namespace std;
#define st first
#define nd second
#define rep(i, a, b) for(int i=(a); i<(b); i++)
#define sz(x) (int)x.size()
#define de(x) cout<< #x<<" = "<<x<<endl
#define dd(x) cout<< #x<<" = "<<x<<" "
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;

const int N = 666;
int n, m, top;
int u[N], sta[N];
ll c[N][N];
char s[N];

int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) {
        scanf("%s", s+1);
        for(int j = 1; j <= m; j++)
            u[j] = (s[j] == '1')? u[j]+1: 0;
        top = 0;
        sta[top++]=0;
        for(int j = 1; j <= m+1; j++) {
            while(u[sta[top-1]] > u[j]) {
                ++c[max(u[sta[top-2]], u[j])+1][j-sta[top-2]-1];//维护单调上升的栈, 看每个柱块向左和向右的最大延伸距离, 即为宽度
                --c[u[sta[top-1]]+1][j-sta[top-2]-1];            //枚举i为底边, 对高度范围为[max(u[sta[top-2]],u[j])+1, u[sta[top-1]]], 宽度为j-sta[top-2]-1的矩形加1
                --top;
            }
            while(top && u[sta[top-1]] == u[j]) --top;
            sta[top++] = j;
        }
    }
    for(int i = 2; i <= n; i++) for(int j = 1; j <= m; j++) c[i][j] += c[i-1][j]; //c1[i, j]: 高为i (n^2) 的连通块, 只统计最长宽度的。
    for(int i = 1; i <= n; i++) {
        for(int j = m-1; j; j--) c[i][j] += c[i][j+1];    //c2[i, j]: 高i宽 >= j的连通块的个数
        for(int j = m-1; j; j--) c[i][j] += c[i][j+1];  //c3[i, j]: 高i宽j的全1矩阵的个数
    }
    for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++) printf("%lld%c", c[i][j], " \n"[j == m]);
    return 0;
}
/*
3 3
011
110
110
如何得到c1? 暴力的话, c1是枚举n^2的上下边界, 优化后, 变成枚举直方图的最底边，快速统计各个不同的上顶边。这个可以通过单调栈+差分解决。求前缀和后就得到c1。
总的时间复杂度为O(nm).
c1
0 3 0
1 1 0
1 0 0
c2
3 3 0
2 1 0
1 0 0
c3
6 3 0
3 1 0
1 0 0

*/

 

 

Wannafly挑战赛12 D

题意：1e9*1e9的01矩阵，1的个数c个(c <= 5000)，统计全0矩阵的个数。

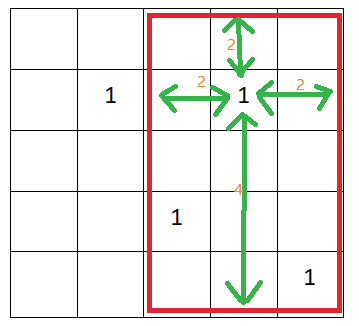
题解：所有情况 减去 包含1的。包含1的矩阵这么算：对于每个1，统计包含这个1而不包含之前的1的矩阵个数。思想类似于带禁手的马跳棋盘方案数计数。时间复杂度 O(c^2)

 

 

#include<bits/stdc++.h>
using namespace std;
#define st first
#define nd second
typedef long long ll;
const int mod = 1e9+7;
pair<int, int> s[5111];
int main() {
    int n, m, c;
    scanf("%d%d%d", &n, &m, &c);
    for(int i = 1, x, y; i <= c; i++) scanf("%d%d", &x, &y), s[i] = {x, y};
    sort(s+1, s+c+1);
    long long ans = 0;
    for(int i = 1; i <= c; i++){
        int l = 0, r = m+1;
        for(int j = i-1; ~j; j--){                                                            //从下往上从左往右枚举之前的点
            ans += (r-s[i].nd)*(n-s[i].st+1LL)%mod*(s[j+1].st-s[j].st)%mod*(s[i].nd-l)%mod;    //上边界为s[j].st ~ s[j+1].st
            ans %= mod;
            if(s[j].nd > s[i].nd) r = min(r, s[j].nd);
            if(s[j].nd < s[i].nd) l = max(l, s[j].nd);
        }
    } 
    //n*m矩阵的子矩阵个数 = 左右两边界 * 上下两边界 
    long long cnt = (n*(n+1LL)/2%mod)*(m*(m+1LL)/2%mod)%mod;
    ans = (cnt-ans)%mod;
    if(ans < 0) ans += mod;
    printf("%lld\n", ans);
    return 0;
}

 

Codeforces 713D Animals and Puzzle

题意：一个n*m的01矩阵，Q个询问，每次询问一个矩形区域内，最大的全1正方形的边长是多少？

题解：dp[0][0][i][j]表示以(i, j)为右下角的正方形的最长边长。RMQ后，二分答案即可。

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1e3+10;
int x1, y1, x2, y2, n, m;
int a[N][N];
int dp[10][10][N][N];
int Log[N];
int ask(int x1, int y1, int x2, int y2){
    int k1 = Log[x2-x1+1], k2 = Log[y2-y1+1];
    int ans = max(dp[k1][k2][x1][y1], dp[k1][k2][x1][y2-(1<<k2)+1]);
    ans = max(ans, dp[k1][k2][x2-(1<<k1)+1][y1]);
    ans = max(ans, dp[k1][k2][x2-(1<<k1)+1][y2-(1<<k2)+1]);
    return ans;
}
bool test(int l){
    //dp[0][x1][y1] dp[0][x2-x+1][y2-x+1]
    int ret = ask(x1+l-1, y1+l-1, x2, y2);
    return ret >= l;
}
void init(){
    for(int i = 1; i <= Log[n]; i++)
        for(int x = 1; x+(1<<i)-1 <= n; x++)
            for(int y = 1; y <= m; y++)
                dp[i][0][x][y] = max(dp[i-1][0][x][y], dp[i-1][0][x+(1<<i-1)][y]);
    for(int i = 0; i <= Log[n]; i++)
        for(int j = 1; j <= Log[m]; j++)
            for(int x = 1; x+(1<<i)-1 <= n; x++)
                for(int y = 1; y+(1<<j)-1 <= m; y++)
                    dp[i][j][x][y] = max(dp[i][j-1][x][y], dp[i][j-1][x][y+(1<<j-1)]);
}
int main(){
    for(int i = 2; i < N; i++) Log[i] = Log[i>>1]+1;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++){
            scanf("%d", &a[i][j]);
            if(a[i][j] == 0) dp[0][0][i][j] = 0;
            else{
                int len = min(dp[0][0][i-1][j], dp[0][0][i][j-1]);
                dp[0][0][i][j] = len+a[i-len][j-len];
            }
        }
    init();

    int t; scanf("%d", &t);
    while(t--){
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        int L = 0, R = min(x2-x1+1, y2-y1+1);
        while(L < R){
            int M = L+R+1 >> 1;
            if( test(M) )
                L = M;
            else
                R = M-1;
        }
        printf("%d\n", L);
    }
    return 0;
}