Person Re-identification 系列论文笔记（五）：SVD-net

SVDNet for Pedestrian Retrieval

Sun Y, Zheng L, Deng W, et al. SVDNet for Pedestrian Retrieval[J]. 2017.
a spotlight at ICCV 2017

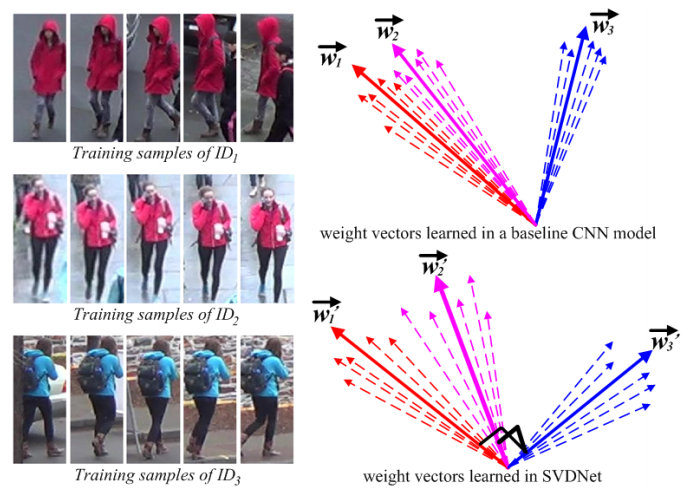
　　这篇的出发点是全连接层的权值相关性分析，作者认为全连接层的作用可以看做一组向量投影。当权值直接相关性较高时（可以理解为权值冗余），特征差异小，直接导致检索中距离差异小，无法获取差异化的特征。

作者提出用SVD对降维层进行操作，提高权值矩阵的正交性，从而提高检索性能。但整个算法流程中，需要人工操作的地方很多，导致整个流程非常不自然。性能不错，但实际操作起来需要过多的人工干预，倒不如将正交性做成一种正则，添加到训练中。

有兴趣的可以看看这篇论文《All You Need is Beyond a Good Init: Exploring Better Solution for Training Extremely Deep Convolutional Neural Networks with Orthonormality and Modulation》。

contributions

　　提出对全连接层进行SVD，让权值向量正交化从而减少冗余，提高检索性。

 

SVD简介

A是m*n的矩阵且rank(A)是k，A的SVD如下：

其中，U是m*m的正交阵，U的列向量称为A的左奇异向量，V是n*n的正交阵，V的列向量称为A的右奇异向量， 是m*n的对角阵，对角线上的值称为A的奇异值。

SVD物理意义

借用《数学之美》中的解释，

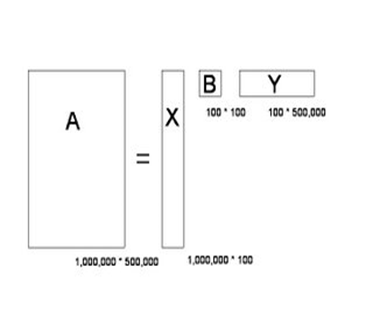
奇异值分解是把一个大矩阵，分解成三个小矩阵相乘。比如把上面的例子中的矩阵分解成一个一百万乘以一百的矩阵X，

一个一百乘以一百的矩阵B，和一个一百乘以五十万的矩阵Y。这三个矩阵的元素总数加起来也不过1.5亿，

仅仅是原来的三千分之一。相应的存储量和计算量都会小三个数量级以上。

三个矩阵物理含义：X中的每一行表示意思相关的一类词，其中的每个非零元素表示这类词中每个词的重要性（或者说相关性），数值越大越相关。

Y中的每一列表示同一主题一类文章，其中每个元素表示这类文章中每篇文章的相关性。中间的矩阵则表示类词和文章类之间的相关性。

因此，我们只要对关联矩阵A进行一次奇异值分解，w 我们就可以同时完成了近义词分类和文章的分类。（同时得到每类文章和每类词的相关性）。

SVD-net pipeline

将倒数第二个FC层（如果是最后一个FC会出现不收敛，有可能是最后一层FC是由样本分布决定）进行SVD，且bias设置为0（bias会破坏正交性），测试特征用输入前的特征会更好一点（经过测试得到的结论）。

RRI训练步骤：

相关性指标S（W）

 

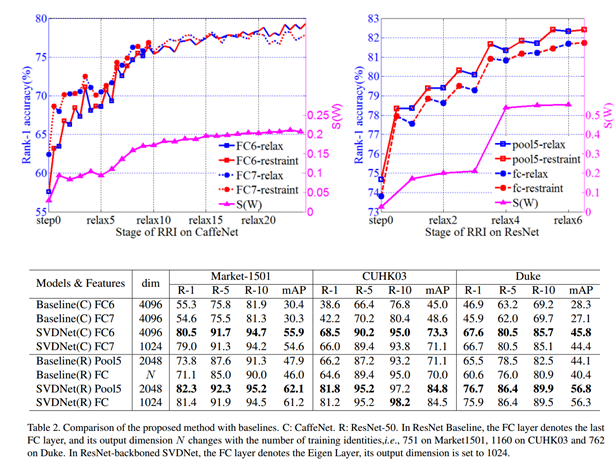
 experiments