支持向量机（support vector machine）-待续

1.支持向量机的概述

支持向量机（support vector machine,SVM）是一种二类分类模型。它的基本模型是定义在特征空间上的间隔(magrin)最大的线性分类器，间隔最大使它有别于感知器(perceptron)；支持向量机还包括核技巧，这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化，可以形式化为一个求解凸二次规划（convex quadratic programming）的问题，也等价与正则化的合页损失函数的最小化问题。支持向量机的学习算法就是求解凸二次规划的最优算法。

支持向量机学习方法由简至繁的模型有：线性可分支持向量机（硬间隔最大化）、线性支持向量机（软间隔最大化）以及非线性支持向量机（软间隔最大化+核技巧，核技巧将输入空间映射到可线性可分的特征空间）。

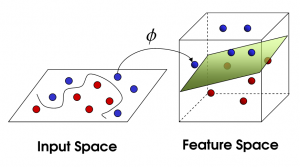
当输入空间为欧式空间或离散集合、特征空间为希尔伯特空间(Hilbert space）时，核函数表示将输入从输入空间映射到特征空间得到的特征向量之间的内积。通过使用核函数可以学习非线性支持向量机，等价于隐式地在高维的特征空间中学习线性支持向量机。这样的方法称为核技巧(Kernal method)。

Cortes 与Vapnik 提出线性支持向量机，Boser，Guyon与Vapnik又引入核技巧，提出非线性支持向量机。

重要关键词：支持向量机，线性分类器，间隔，凸二次规划，核技巧

下文将从感性和理性两方面分析支持向量机。

2.支持向量机的感性察觉（转自 Iddo和简之）

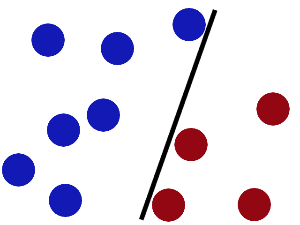
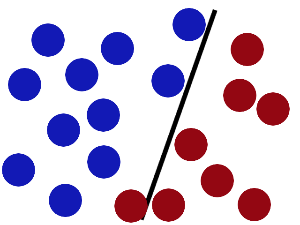
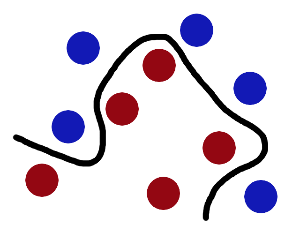
好吧，故事是这样子的：在很久以前的情人节，大侠要去救他的爱人，但魔鬼和他玩了一个游戏，魔鬼在桌子上似乎有规律放了两种颜色的球，说：“你用一根棍分开它们？要求：尽量在放更多球之后，仍然适用。”

　　于是大侠这样放，干的不错？

　　然后魔鬼，又在桌上放了更多的球，似乎有一个球站错了阵营。

　　SVM就是试图把棍放在最佳位置，好让在棍的两边有尽可能大的间隙（最大间隔）。

　　现在即使魔鬼放了更多的球，棍仍然是一个好的分界线。

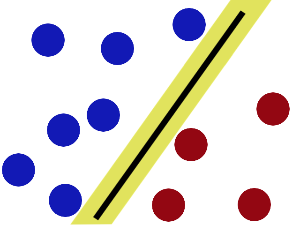
　　然后，在SVM 中有另一个更加重要的 trick。魔鬼看到大侠已经学会了一个trick，于是魔鬼给了大侠一个新的挑战。

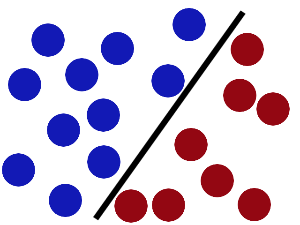
　　现在，大侠没有棍可以很好帮他分开两种球了，现在怎么办呢？当然像所有武侠片中一样大侠桌子一拍，球飞到空中。然后，凭借大侠的轻功，大侠抓起一张纸，插到了两种球的中间。

　　现在，从魔鬼的角度看这些球，这些球看起来像是被一条曲线分开了。

　　再之后，无聊的大人们，把这些球叫做 「data」，把棍子叫做 「classifier」, 最大间隙trick 叫做「optimization」，拍桌子叫做「kernelling」, 那张纸叫做「hyperplane」。

　　数据线性可分时那么如何确定这个超平面（hyperplane）?数据线性不可分时如何运用核技巧（kernelling）?

3.支持向量机理性挖掘

　　这一节将分析支持向量机的理论基础，涉及的主要内容有：感知机、间隔最大化、凸二次规化、线性可分支持向量机、线性支持向量机以及非线性支持向量机。

3.1 感知机

感知机是二类分类的线性分类器，其输入为实例的特征向量x，输出为实例的类别y，取+1和-1二值，感知机对应与输入空间中将实例划分为正负两类的分离超平面，属于判别模型，感知机1957年由Rosenblatt提出，是支持向量机的基础。其决策函数为

　其中分离超平面为：　；w,b取值的过程遵循极小化损失函数：，M为误分类点的集合，损失函数为对应于误分类点到分离超平面的总距离。

　　可以看出感知器追求的目标：误分类点尽可能的少（构造的损失函数不连续，不易优化），将其转化为损失函数连续的“误分类点到超平面的总距离最小”。很容易判断：当训练数据集线性可分时，感知机有无数多个，即w,b有无数个组合，那么到底哪个感知机是最好的呢？用什么标准来评价好与坏了？下面我们用几何间隔来评价分类器的好坏，介绍线性可分支持向量机。

3.2 线性可分支持向量机

假设一个数据集可以用一个超平面分割成两类，超平面的方程为：，符合该条件的超平面有无数多个，线性可分支持向量机利用间隔最大化求唯一且存在的最优分离超平面：，这里的最优的标准就是间隔最大化，什么是间隔呢？其实就是实例点到超平面的距离的最小值（几何间隔）。

3.2.1 分类正确性及确信度的表征变量-间隔

　　间隔用于评价分类器好坏的，给定一个超平面，我们知道能过相对地表示点x距离超平面的远近。的符号与类标记y的符号是否一致能够表示分类是否正确，所以可以用变量定量表征分类的正确性及确信度，这就是函数间隔的概念，容易看出，当w,b成比例变化时，超平面没有变化，但函数间隔却随之成比例变化，因此引入了集合间隔来改善函数间隔，几何间隔为min{}，其物理意义为：被正确分类的实例点到超平面的距离或被误分类点到超平面距离的相反数。我们运用间隔来量化表征分类点的正确性及确信度，间隔是正数，说明实例点被正确分类，相反，则被误分类；间隔越大，则正确的置信度越大。由上述论述很容易推理到怎么样的分类器是最好的：所有点到超平面的几何间隔之和最大对应的超平面是最好的分类器。这便是支持向量机的思想。概括如下：对训练数据集找到几何间隔最大的超平面作为分类器，这意味着以充分大的确信度对训练数据进行分类。也就是说，不仅将正负实例点分开，而且对最难分的实例点也有足够大的确信度将它们分开，这样的超平面应该是对未知的新实例有很好的分类预测能力。

3.2.2 对应的最优化模型

（1）

　　其中为几何间隔

为了简化优化模型，我们不妨设函数间隔为=1，由函数间隔与几何间隔的关系：==，目标函数变为最大化，等价于最小化，上述最优化问题故可以转化如下形式：

（2）

其中yi,xi是训练集数据，为已知，待优化的决策变量为确定超平面的参数:法向量w以及常数b。线性可分训练数据集的最大间隔分离超平面是存在且唯一的，即上述优化问题是存在唯一的一个最优解的。

上述优化问题为标准的凸二次规划问题。凸优化问题为一下约束最优化问题：

　　其中，目标函数和约束函数在Rⁿ连续可微的凸函数，约束函数是Rⁿ上的仿射函数（）

3.2.3 线性可分支持向量机学习算法

由（2）式优化模型，构造最大几何间隔的分离超平面，，求解凸二次规划有许多成熟的算法，这里不详细介绍求解算法，对偶算法有较高的效率，其涉及运用拉格朗日对偶性的知识点，可以查看该博客；
解得，，其中由以下对偶问题求得：

并且有对应与>0的样本点（x_i,y_i）的实例为支持向量，这一点可以由拉格朗日函数及KKT条件看出。
确定分类决策函数，完成分类器构造。

3.2.4 支持向量机的命名和特征

　　谈了这么多，支持向量机为啥这样命名，在线性可分的情况下，训练样本的样本点与分离超平面距离最近的样本点的实例称为支持向量。支持向量是使约束条件等号成立的点，即

　　其中H1和H2为支持向量所在的平面，即满足方程的两个超平面和，可以看出，在决定分离超平面时只有支持向量起作用，而其他点不起作用，由于支持向量在确定分离超平面中起着决定性的作用，所以讲这种分类模型称为支持向量机。

得到的支持向量机有以下性质：

函数间隔为1；
几何间隔为；
支持向量据超平面的距离为.

3.3 线性支持向量机

　　前面我们介绍了线性可分支持向量机，其特点是可以用一个分离超平面将两类实例点完全隔开，而且对应的几何间隔最大。实际中的点一般为线性不可分，即实例点不能满足函数间隔大于等于1的约束条件，为了解决这个问题，我们对每个样本点引入一个松弛变量，使得函数间隔加上松弛变量大于等于1.（每个实例点对应的松弛变量的值不是一样的，可以为0，代表该实例点不需要松弛变量），见下图，以i=1的实例点分析，该点到超平面的几何距离为负值，加上几何距离，才能等于（对应为函数间隔加上松弛变量等于1），该实例点为软间隔的支持向量。