11.6.1 基础

动量法之所以叫动量法的原因：实际上是在维护一个动量，从而让每一次改变（由于惯性）不改变太多，减少震荡

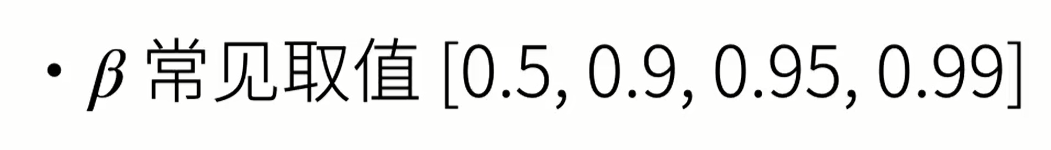
有效样本权重那里，翻译有错误。原文说的是在（随机）梯度下降中将\(\eta\)变为\(\frac{\eta}{1-\beta}\)，而不是在动量法中。这样子做相当于在（随机）梯度下降中模拟了一个近似的动量法。但是有效样本权重真正的意思见下

动量法其实用的是一个叫做指数加权平均的技术
指数加权平均就是给定一个如下的序列

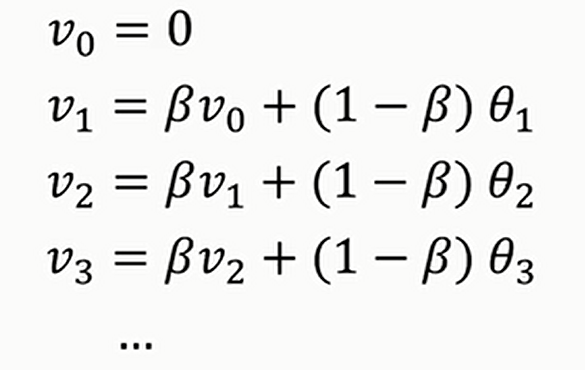
对于\(v_i\)，其计算的是

\[\theta_{i-\frac{1}{1-\beta}} \]

到

\[\theta_i \]

的平均值
原因：利用公式\(\underset{x\rightarrow0^+}{\lim}(1-x)^{\frac{1}{x}}=e^{-1}\)，写出\(v_i\)的通项公式之后就可以知道，我们只用考虑\(i\)前面\(\frac{1}{1-\beta}\)项就好了，其余的项基本可以忽略
但是这里会存在一个问题，当\(i\)比较小的时候，可能无法进行正确估计，比如当\(\beta=0.98\)的时候，可以计算一下\(v_2\)，不能正确估计\(\theta_1\)和\(\theta_2\)的平均值（两者的系数都太小了），这个时候要进行修正，即\(v_i^{'}=\frac{v_i}{1-\beta^i}\)（当\(t\)比较大的时候，这个修正显然就无效了）

另一个理解动量法的视角见下
动量梯度下降就要用到前面的加权平均法了

如上图，普通的梯度下降法可能会震荡，导致接近最优值的速度很慢；可是如果我们进行平均了，\(y\)方向的正负向量就抵消了，\(x\)方向的正向量相加

就可以像上图红线一样快速接近最优值了

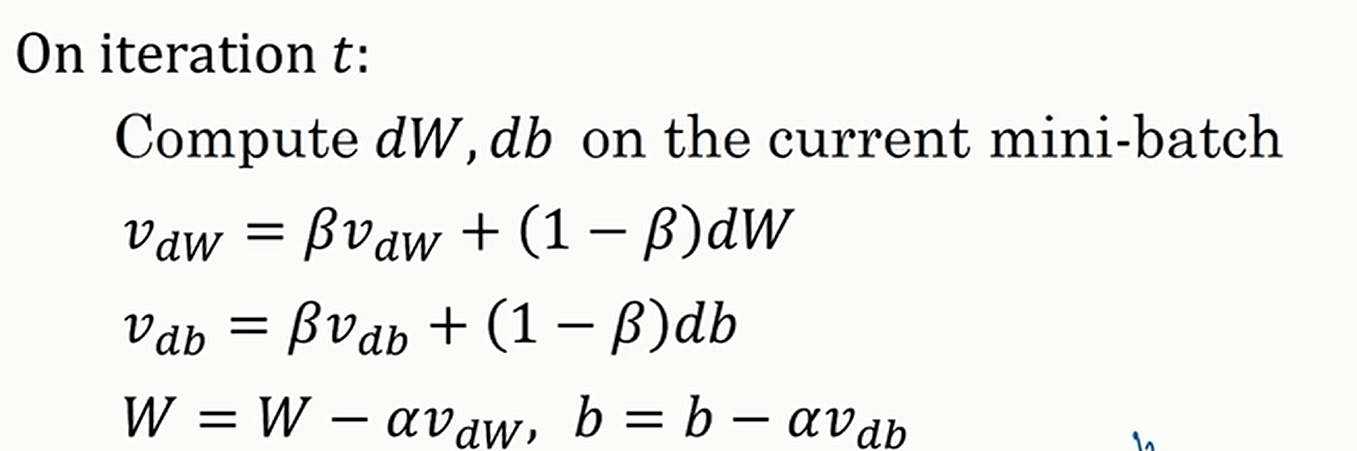
一般来说\(\beta=0.9\)；一般不会进行偏差修正，因为仅仅迭代十次之后就已经不怎么存在偏差了，所以几乎没有人会做偏差修正

如果有多层的话，更新公式见下

\[ \begin{cases} v_{dW^{[l]}} = \beta v_{dW^{[l]}} + (1 - \beta) dW^{[l]} \\ W^{[l]} = W^{[l]} - \alpha v_{dW^{[l]}} \end{cases}\tag{3}\]

\[\begin{cases} v_{db^{[l]}} = \beta v_{db^{[l]}} + (1 - \beta) db^{[l]} \\ b^{[l]} = b^{[l]} - \alpha v_{db^{[l]}} \end{cases}\tag{4}\]

注意：

• 速度用零初始化。因此，算法需要几次迭代来“积累”速度并开始采取更大的步骤。
• 如果\(β=0\)，那么这就变成了没有动量的标准的梯度下降。

如何选择\(\beta\)？

• 动量\(\beta\)越大，更新越平滑，因为我们更多地考虑过去的梯度。但如果\(\beta\)太大，它也可能使更新过于平滑。
• \(\beta\)的常见值范围从\(0.8\)到\(0.999\).如果你不想调整这个值，\(\beta=0.9\)通常是一个合理的默认值。
• 为你的模型调整最优的\(\beta\)可能需要尝试几个值，以查看哪个值在减少成本函数\(J\)的值方面效果最好。

你应该记住的要点：

• 动量考虑过去的梯度以平滑梯度下降的步骤。它可以应用于批量梯度下降、小批量梯度下降或随机梯度下降。
• 你必须调整动量超参数\(\beta\)和学习率\(\alpha\)。