这道题目虽然是放在容斥原理题单里面的,但实际上用的是二项式反演(当然这东西也是由容斥原理推导出来的)
但是啦我已经很满足了,我自己已经推出了大部分的式子了,只是最后不会二项式反演而已
这种没什么思路的题目,我们先从小范围开始想起
我们假设只有一门课,那么我们从个同学中选出个人(),表示这些人被B神碾压,那么剩下的个人的成绩都严格大于B神。我们假设B神的成绩是,那么答案就是(注意要满足B神的排名与被碾压的人数不矛盾)
现在我们来看看有两门课。我们先从第一轮考虑,我们先选出个人()表示这些人的成绩严格大于B神,那么剩下的个人就是在这门课中成绩没有超过B神的人。那么我们对第二门课做同样的操作,然后我们来判断是否符合条件。我们发现,当一个人在两门课都没被选择的时候,他才会被B神碾压,也就是说,我们设第一门课中选出的个人的集合是,第二门课选出的个人的集合是,那么我们需要满足
然后我们推广到三门课,有,然后我们就可以推广到门课了
也就是说,先选择个人表示这个人不在任何一个里面,而且最后要有
我们先选择个人,很显然,为
然后我们来考察满足的所有的方案数,这东西就要用到二项式反演了。有关二项式反演
然后我们发现我们整体的结构就已经确认好了。假设我们现在已经有了B神的成绩,分别为,那么选出的个人的第门课的成绩就有种选择,没被选出来的个人第门课的成绩就有种选择,我们根据乘法原理乘起来就好了(这其实是非常重要的一个点,感觉很多容斥的题目,或者说计数的题目,当结构不同的时候,贡献是一样的,所以我们只用计算结构的数量就好了,比如这道题目,我们并不关心这个人具体是谁,因为只有数量是一样的,贡献就一样)
但是还有个问题,我们不可能枚举每一个,这个时候就可以看这篇题解
update 2024.5.3
没想到我居然把所谓的二项式反演自己推出来了。。还是挺开心的(当然具体的二项式反演还没有学,有空了学一下)
最后放的那篇题解有笔误,下文会说明
首先老规矩,跟上文叙述的思考过程一样,直接跳到二项式反演那里
其实现在就是要在剩下的个人当中分配成绩,使得不存在任何一个人被B神碾压而且每门课都符合B神的排名
我们先忽略不被B神碾压的条件,来考虑每门课都符合B神的排名的所有的情况
那么总数显然就是。这个式子的意思是,依次考虑每门课,对于当前考虑的这门课,选出个人,这些人的成绩严格大于B神
然后用容斥减掉不合法的情况。设表示这个人中第个人被B神碾压的方案的集合,那么答案就是用上面说的总数减去
后面那个式子用容斥原理展开即得
其中是上界
这个式子的意思是,我们从个人中选出个人来表示这个人被B神碾压(),并且枚举他们的成绩(),然后在按照最开始的选法依次考虑每一门课()即可
然后将三部分化简之后得到答案
然后三个部分分别计算就好了
然后最后一个问题就是我们不可能枚举B神的成绩,怎么办?
实际上利用最后贴的题解就好了
我们只考虑某一门课,假设我们已经定下来了所有人的成绩,分别是,那么统计中不同数字有多少个,记为个,那么这个数字肯定可以从个数字中选出,即,然后我们就可以建立一个映射了。也就是说我们枚举,从个数中选出个数,然后让所有人的成绩只能从这个数中选择,把所有情况加起来就是答案了。但是我们直接枚举的话不能保证我们选取了个数之后,这个数的每一个数都会被选择,此时要用题解中说的容斥去解决(而且这个容斥挺新的,可以学一学)。但是题解中的公式错了,
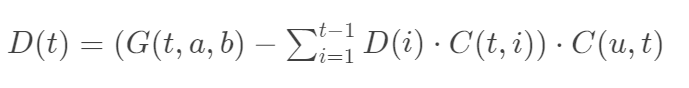
这个最后不要乘以,而是在统计答案的时候乘以,可以想一下为什么,具体见代码
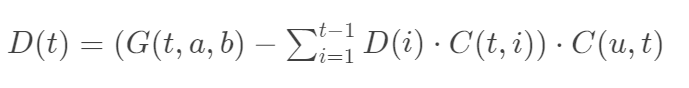





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构