One-X
这里肯定考虑每个点作为lca对答案的贡献
考虑点\(p\)，所代表的区间长度为\(l\)，那么其左右两个子树的叶子节点一定至少选一个，即贡献为$$p \times (2^{\lfloor \frac{l}{2} \rfloor}-1)\times (2^{\lceil \frac{l}{2} \rceil}-1)$$，其中\(\lceil \frac{l}{2} \rceil\)和\(\lfloor \frac{l}{2} \rfloor\)分别为左右子树所代表的区间长度，减一是因为要去掉一个叶子都不选的情况
然后有一个结论，线段树每层的不同区间的长度至多相差一
考虑用数学归纳法证明，假设对第\(i\)层，代表长度为\(l\)和\(l-1\)，那么第\(i+1\)层的长度就是\(\lfloor \frac{l}{2} \rfloor,\lceil \frac{l}{2} \rceil,\lfloor \frac{l-1}{2} \rfloor,\lceil \frac{l-1}{2} \rceil\)，根据\(l\)的奇偶讨论即可
那么我们储存每一层的区间的长度，以及每一种区间长度的区间的个数，以及对应的节点的编号和
举个例子，假设线段树的根节点的长度是\(5\)，处于第一层，那么第三层就有四个节点，分别为\((4,[1,2]),(5,[3,3]),(6,[4,4]),(7,[5,5])\)，我们就统计长度为\(2\)的区间有一个，编号和为\(4\)；长度为\(1\)的区间有三个，编号和为\(18\)
那么我们推导下一层的对应信息，就先算出下一层的长度以及对应的区间个数，那么编号和显然一个乘以\(2\)另一个乘以\(2\)再加上区间的个数，可以自己推导一下
这里的推导也启示我们，不用非要记录最终的结果，我们记录结果的每个因子也是可以的
时间复杂度为\(O(log^2n)\)
代码一定也看一下，用了map的迭代器
#include<bits/stdc++.h>
#define ll long long
#define ULL unsigned long long
using namespace std;
const int p=998244353;
ll n;
map<ll,pair<int,int> > mp[100];//mp[i][l]表示第i层区间长度为l的信息
//mp[i][l].first表示长度为l的区间的编号和
//mp[i][l].second表示长度为l的区间的个数
//之所以要用map，是因为区间长度在贡献式子里面为指数部分，不能随意取模
ll quickpow(ll a,ll b)
{
ll res=1;
while(b)
{
if(b&1) res=(res*a)%p;
a=(a*a)%p;
b>>=1;
}
return res;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int res=0;
scanf("%lld",&n);
int lg=__lg(n)+3;
for(int i=1;i<=lg;i++)
mp[i].clear();
mp[1][n]=make_pair(1,1);
for(int i=1;i<=lg;i++)
for(map<ll,pair<int,int> >::iterator it=mp[i].begin();it!=mp[i].end();it++)
{
pair<ll,pair<int,int> > u=*it;
if(u.first==1)
{
res=(res+u.second.first)%p;
continue;
}
ll l=(u.first+1)/2,r=u.first-l;
res=(res+u.second.first*(quickpow(2,l)-1)%p*(quickpow(2,r)-1)%p)%p;
mp[i+1][l].first=(mp[i+1][l].first+u.second.first*2%p)%p;
mp[i+1][l].second=(mp[i+1][l].second+u.second.second)%p;
mp[i+1][r].first=(mp[i+1][r].first+(u.second.first*2%p+u.second.second)%p)%p;
mp[i+1][r].second=(mp[i+1][r].second+u.second.second)%p;
}
printf("%d\n",res);
}
return 0;
}
update 2024.7.12
想到一种新的做法，对于完全二叉树，我们显然可以通过按层统计来得到答案
对于每一层，我们可以算出编号和，而每个节点所代表的区间长度都是一样的，所以可以直接计算
对于非完全二叉树，可以知道左右子树一定有一个是完全二叉树，对于完全二叉树的部分采用上述做法，非完全二叉树部分递归计算即可，时间复杂度仍然是\(O(log^2n)\)
想到这种做法主要还是从考虑贡献+特殊情况入手
update 2024.7.29
上面想出来的新做法是错的，线段树建的树不一定是按照逐个增加节点的方法建的，如下
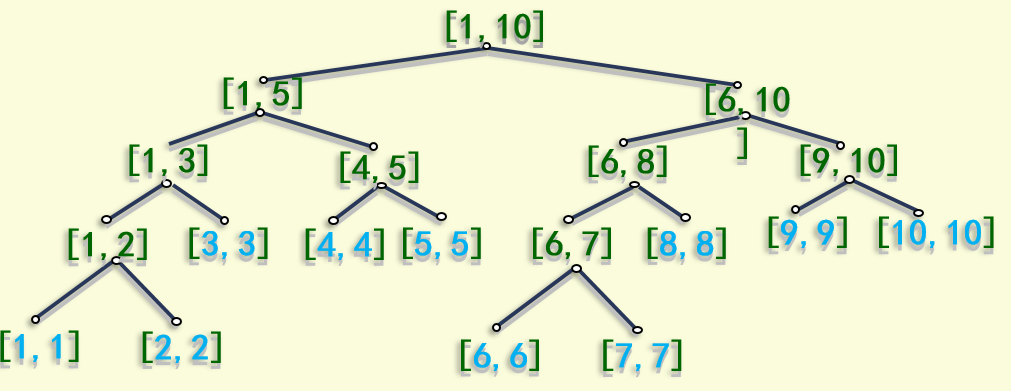
正确思路的原因是，同一长度的节点，建出的树的形态是一样的，可以直接利用长度统计
