珍珠项链

设$f[i][j]$表示用$i$种珍珠构成长度为$j$的项链的种数

如果此时我们以珍珠的种类为考虑对象，枚举第$i$种珍珠的数量，那么有$f[i][j]=\sum _{l=1}^{j-i+1}f[i-1][j-l]\times C_j^l$

会发现这样完全推不走，因为$n$太大了

看到$n$这么大一般都是矩阵乘法，所以我们考虑用矩阵加速递推

由于矩阵快速幂要求向量长度不长但是变化时间很长，所以这里我们要把$i$作为向量长度，$j$作为变化时间，所以要考虑最后一个珠子是什么（这样递推的时候才只会用到$j-1$的数据）（这也是分组DP的常用trick，不去考虑最后一个组是什么，而去考虑最后一组最后一个是什么）

有$f[i][j]=\sum _{k=1}^{i}f[i-1][j-1]+f[i][j-1]=i(f[i-1][j-1]+f[i][j-1])$

前面一项是考虑我最后一个珠子放编号为$k$的珠子而且这个珠子是第一次出现（注意由编号为$1,2,3...k-1,k+1,k+2...i$组成长度为$j-1$的珠子与由编号为$1,2,3...i-1$组成长度为$j-1$的珠子是等价的）

后面一项是我考虑最后一个珠子放编号为$k$的珠子而且这个珠子在前$j-1$个珠子中已经出现过了

现在还有一个问题，就是题目要求的是长度不超过$N$的项链，但是我们求得是刚好等于$N$的，怎么解决？

有两种解决方案，我先讲讲第一种，第二种放到老板的解决方法讲

第一种方法就是改状态：设$f[i][j]$表示用$i$种珍珠构成长度不超过$j$的项链的种数

这时只有$f[1][j]=f[1][j-1]+1$改变了一下，$f[2+][j]$之后的状态转移方程都不变

所以就可以写出一个转移矩阵：

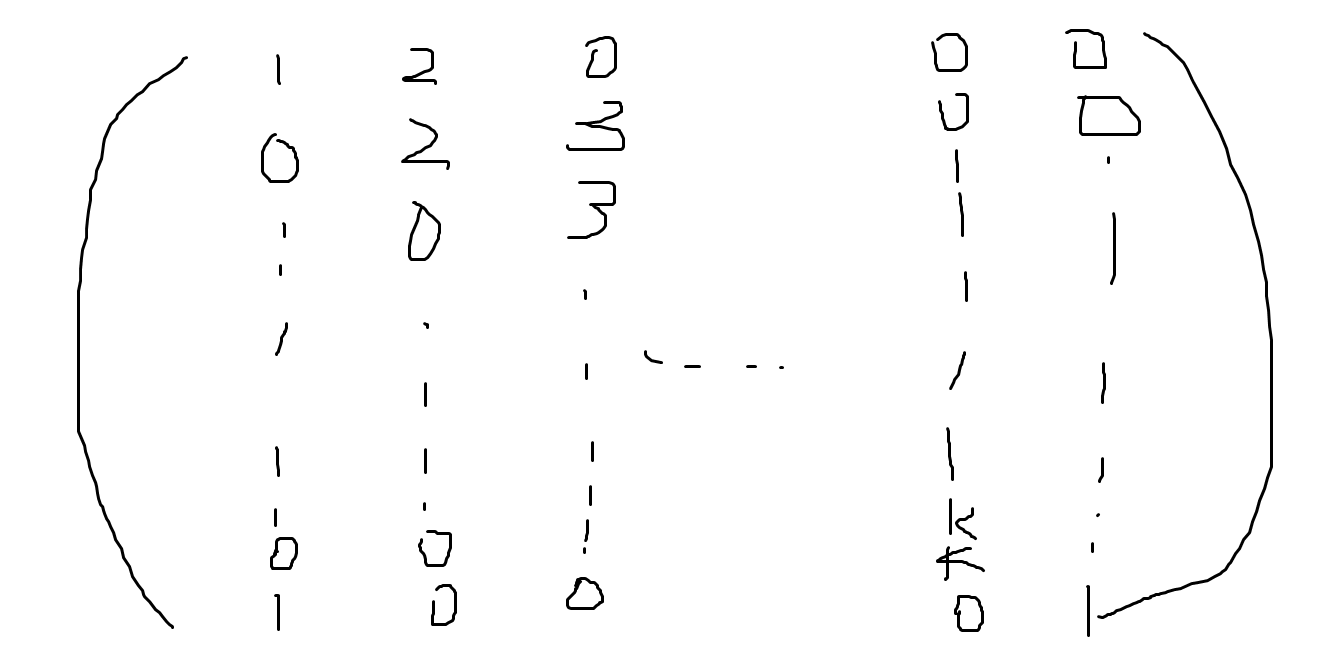
注意这是$k+1$阶矩阵

然后上矩阵快速幂就好了

然后来看看老板的做法

我们的DP状态一般是不会考虑这个状态之外的全局的东西的，他这里考虑了：这里的$j$种珍珠指的是从所有的$k$种珍珠任选$j$种珍珠组成的方案数的总和（比如$(k-(j-1))dp[i-1][j-1]$指的就是已经选了$j-1$种珍珠在前$i-1$个里面，再从剩下的$k-j+1$种珍珠里面选一个放在最后）（这个要从刷表法的角度去理解，这种DP的形式还是比较新了，填表法的形式刷表法的理解）

然后介绍第二种方法：在向量中添加一个元素表示前缀和