逃学的小孩

一个性质：$A$和$B$一定是直径的两端点

这个证明比较简单，我们假设一条非直径路径$DE$，然后随便选一个点作为$C$，通过讨论$AB$与$DE$是否相交即可

当然还有更简单的想法，我们随便找一个点$C$，然后假设$A$和$C$更近，就有最终的长度是$AC+BA$，其中$AC$的长度最长是离$C$最远的点的距离，$BA$的长度最长是直径。而想一下我们是怎么用BFS求直径的：我们随便找一个点，然后找出离这个点最远的点，那么这个点一定是直径的端点，然后找出离这个点最远的点，就找出直径了。而我们最开始随便找的点就认为是$C$的话，如果$A$和$B$刚好是我们找出的另外两个点，那么刚好$AC$和$AB$同时取到最大值，所以我们上述的性质是正确的

所以我们随便找一条直径（当然其实这个东西也需要证明，然而。。。whatever，从考试的角度考虑吧），然后枚举$C$即可

我自己也想到一个办法，我们考虑，我们随便找三个点，那么这三个点一定在一条直线上，$C$在哪呢？$C$肯定是在中间那个点上，于是乎我们可以利用换根DP做这道题目

我们需要知道从每个点出发的最长路径和不严格次长路径，在树形DP的时候，我们分从根节点向下的最/次长和从根节点向上的最/次长即可。自己推到一下状态转移方程

update 2024.5.26

这道题目的证明用“树网的核”的图来证非常easy

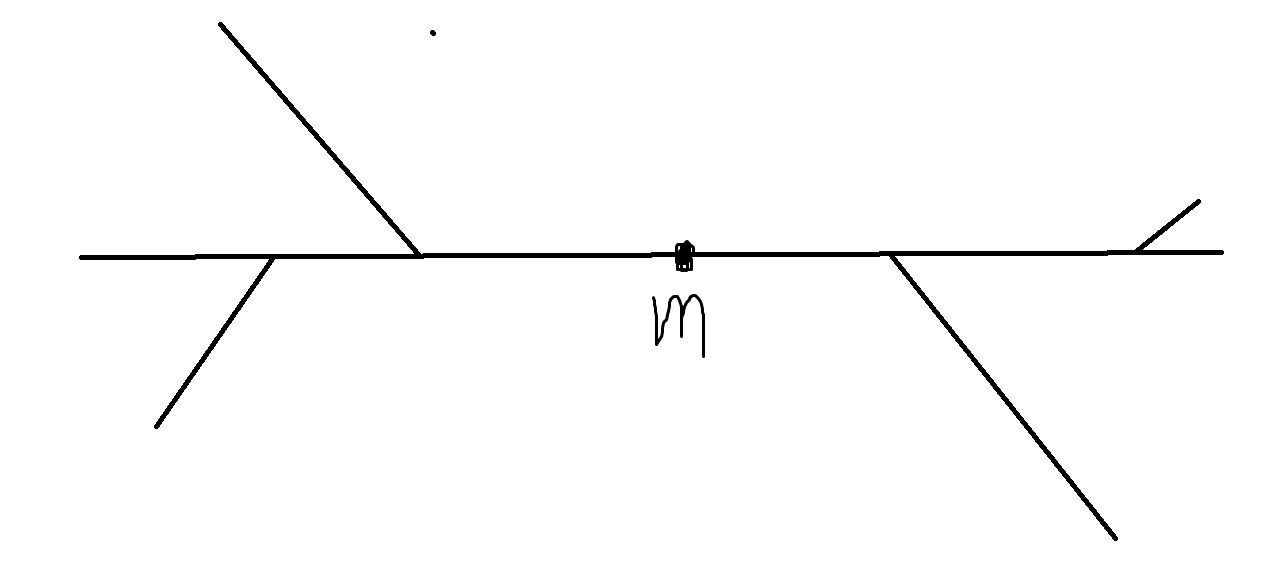
假设$A,B$不是直径的两端，那么$A,B$最多只有一个点在直径的一端，于是再分$C$的位置讨论就好了，比如

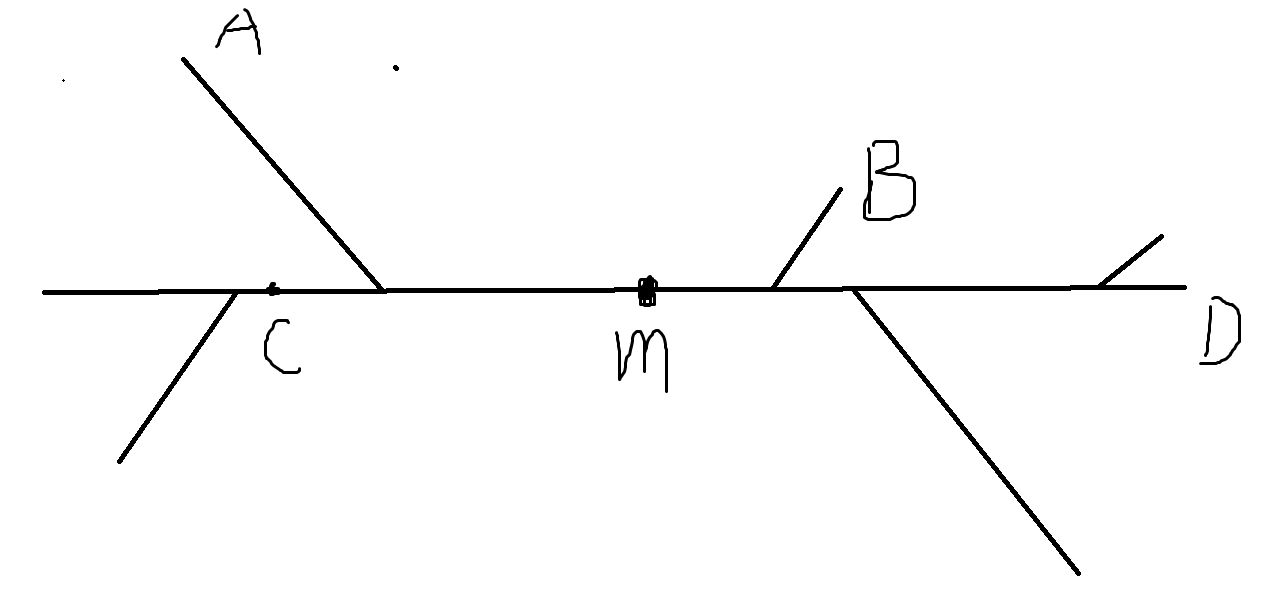
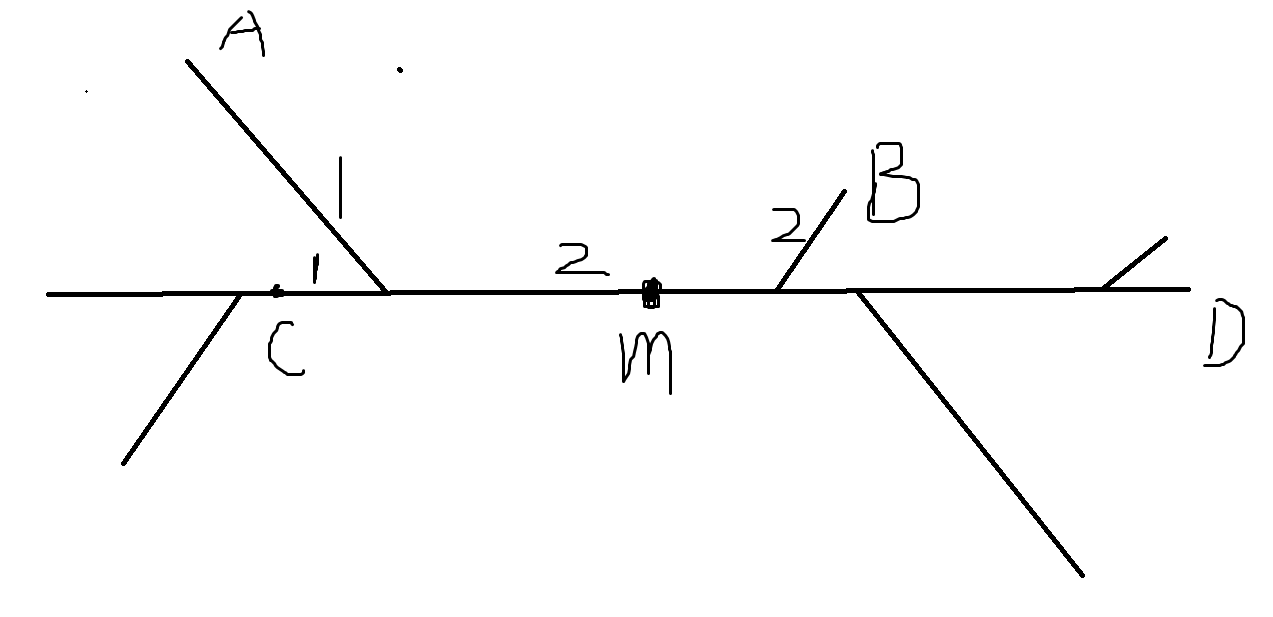
如果说$C$离$A$更近，那么显然将$B$换成$D$答案会更优；如果$C$离$B$更近，那么不换的答案长成这个样子（数字表示边被计算的次数）

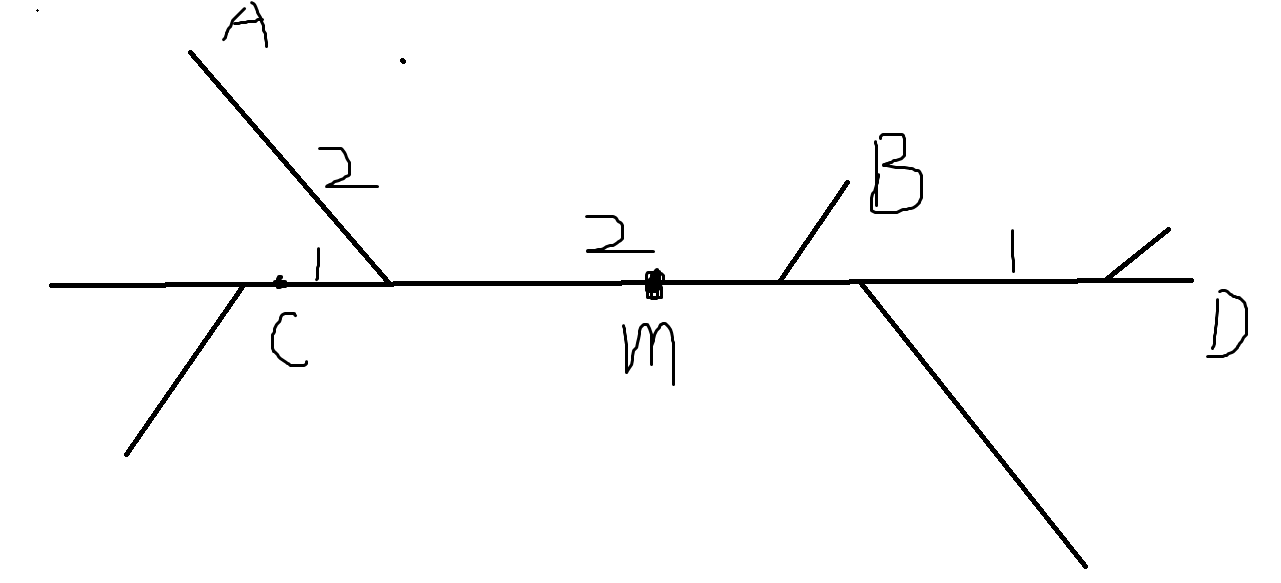
换成$D$之后被计算的次数为

两图相减根据直径的最长性就很容易得出来了

但是我自己的做法我却看不懂了。。。

update 2024.8.17

感觉上面的证明不是很严谨，比如这种情况

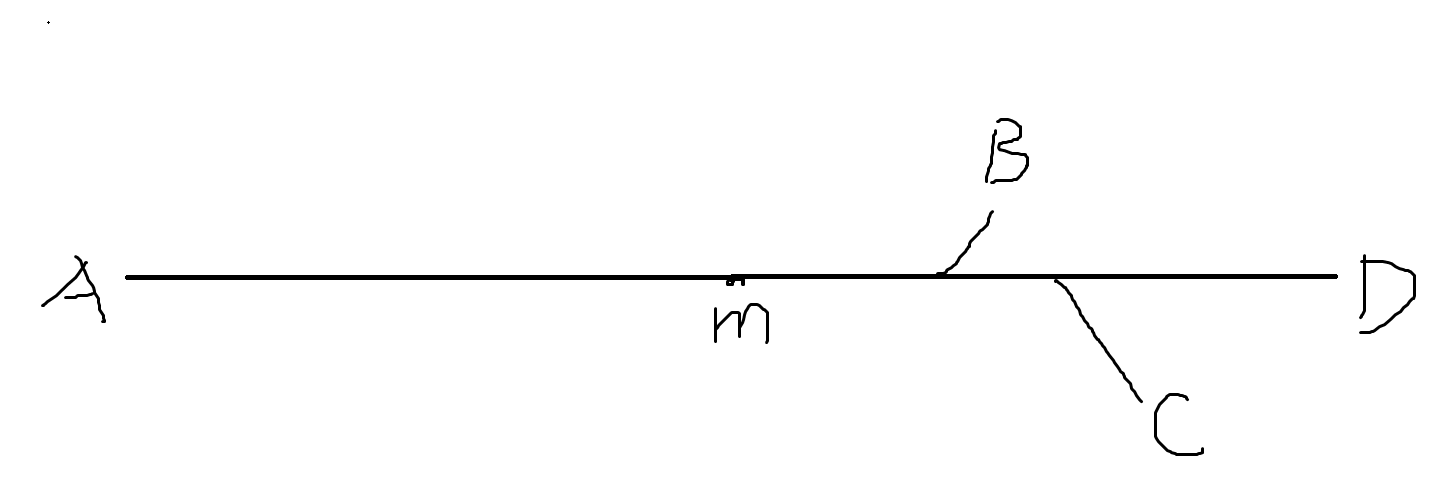
此时必须将$C,B$交换位置之后才可说明$B$换成$D$的距离更长