观光
方法一: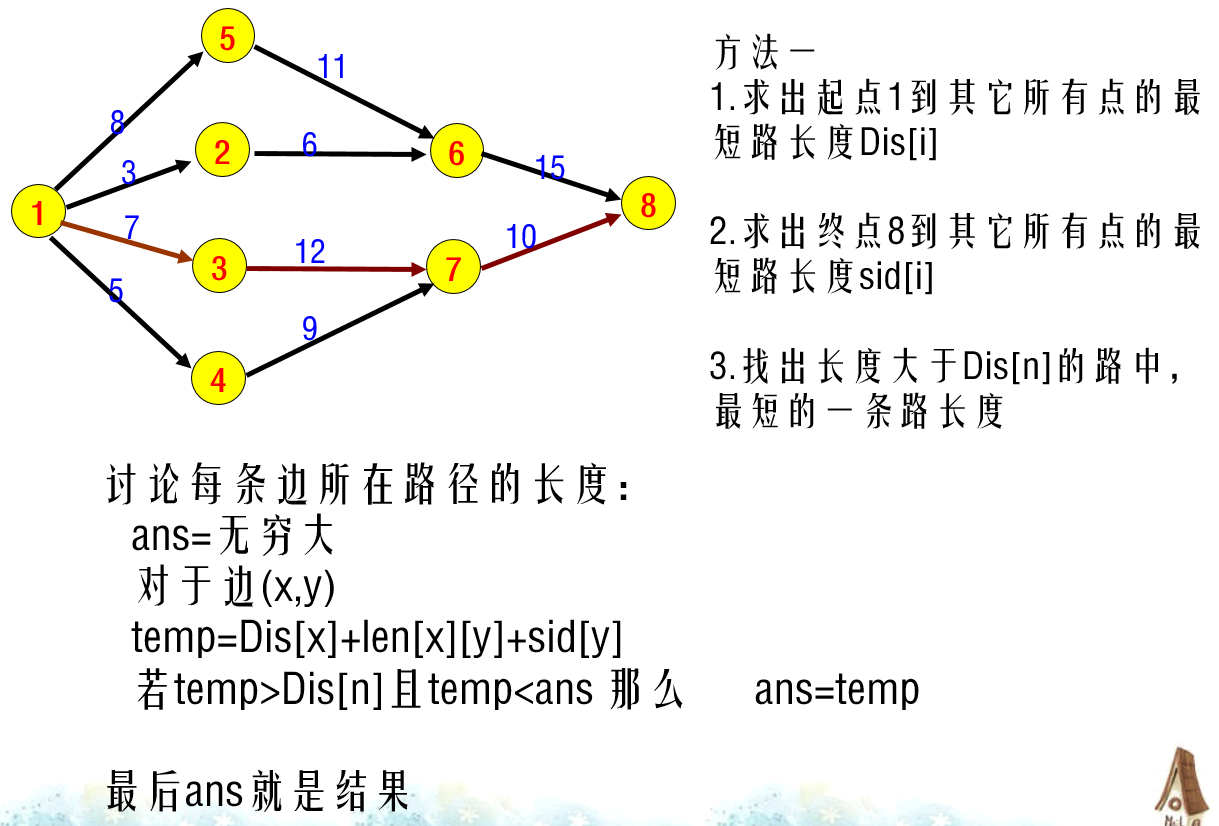
来证明一下为什么一定可以找到严格次短路
显然最终得到的
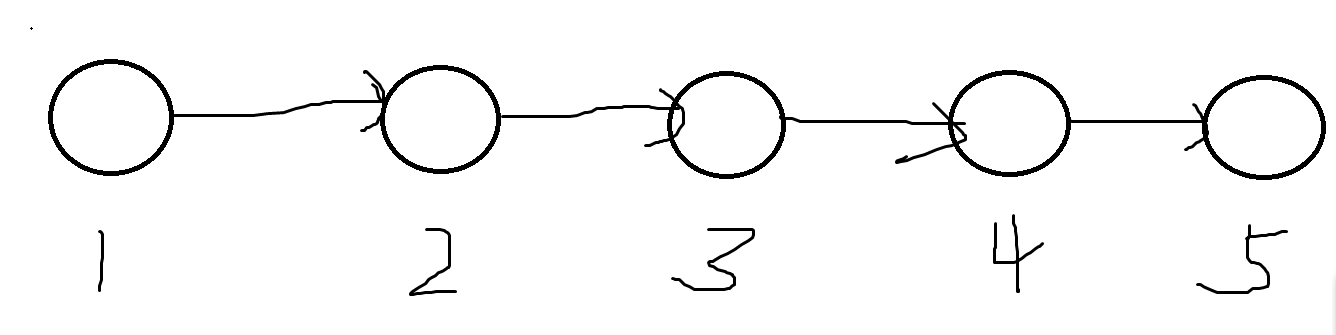
那么我们枚举这条路径上面的边的时候,得到的
我们不妨设我们是依次枚举图中的边的
第一次枚举的是
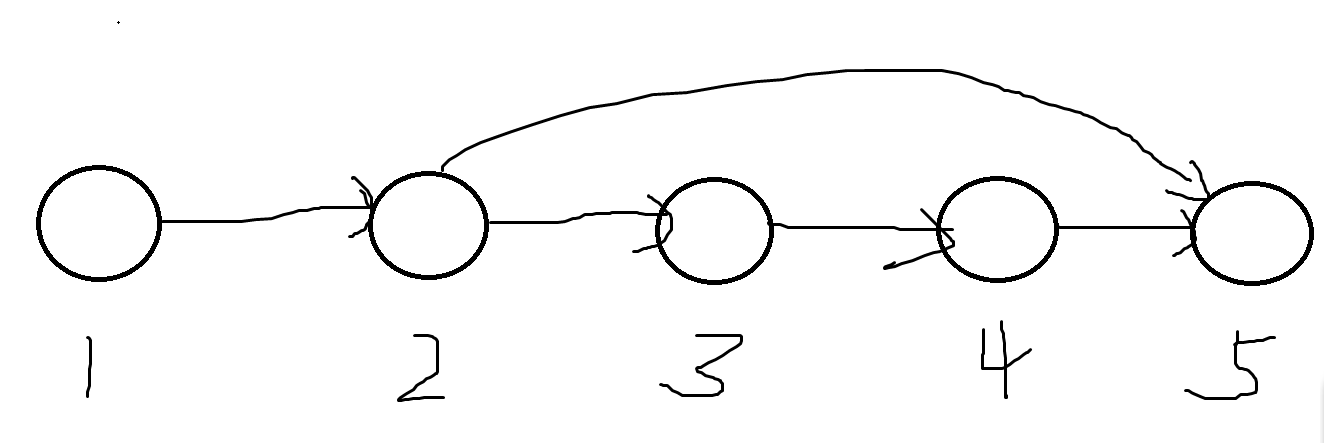
这也说明了
第二次枚举的是
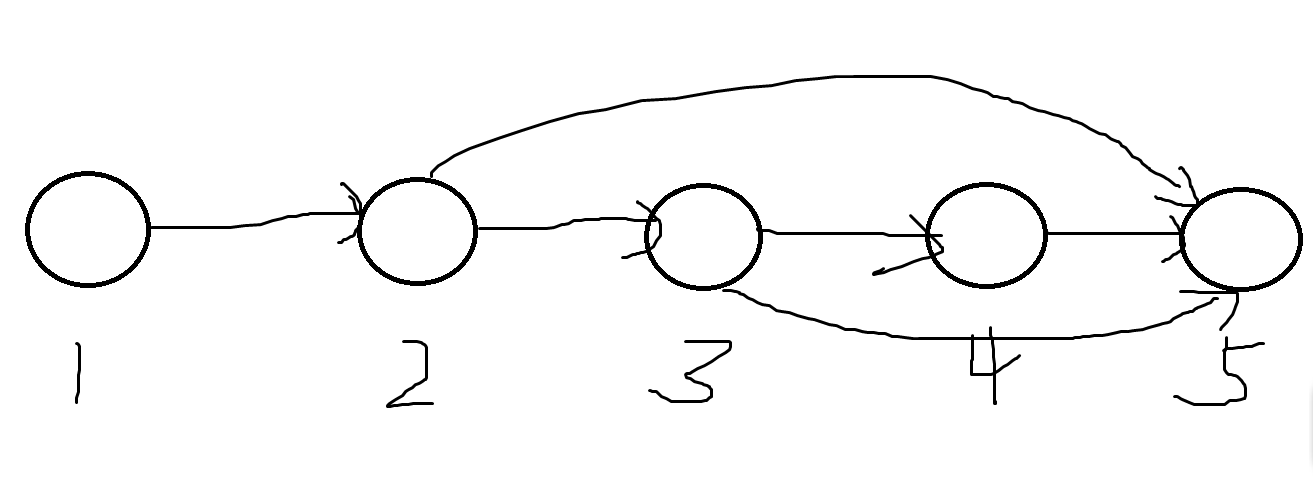
注意
第三次枚举的是
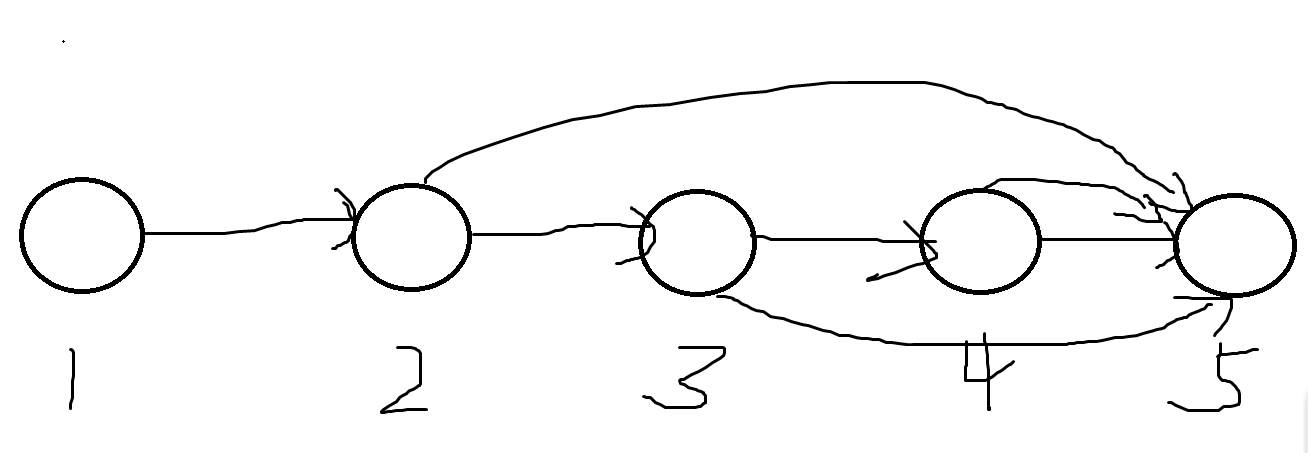
同理说明
然后我们就发现,我们接下来枚举
方法二看这篇题解
方法一:
来证明一下为什么一定可以找到严格次短路
显然最终得到的

那么我们枚举这条路径上面的边的时候,得到的
我们不妨设我们是依次枚举图中的边的
第一次枚举的是

这也说明了
第二次枚举的是

注意
第三次枚举的是

同理说明
然后我们就发现,我们接下来枚举
方法二看这篇题解
【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构