子串

很容易想到一个状态$f[i][j][k]$表示$A$串前$i$个，$B$串前$j$个，从$A$中取了$k$个子串的总方案数

但是稍微推一下状态转移方程就可以知道这个时间复杂度和空间复杂度都会爆炸，其中时间复杂度为$O(n{m}^{2}k)$

空间复杂度可以用滚动数组来优化，所以我们先放下不管，我们先来考虑时间复杂度怎么优化

状态肯定是类似的，没有其他很多的选择，所以我们要微调状态

这个时间复杂度之所以会多一个$m$，就是因为我们在推方程的时候，要枚举互相匹配的$A$末尾的一段与$B$末尾的一段的长度

所以我们微调状态为$f[i][j][k][0/1]$，其中$0$表示不选$A[i]$，$1$表示要选

这样就可以把多一个$m$消掉

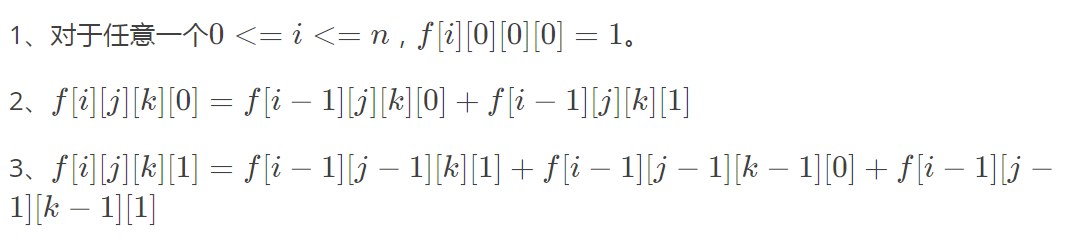
对于$f[i][j][k][1]$，当$k-1$时既可以选$0$也可以选$1$的原因是当前这个位置可以单独作为一个子串，不一定非要跟前面的连起来

然后用滚动数组优化就可以了

总结一下我们目前遇到的微调状态：前$i$个（LCS问题），前$i$个且以$i$结尾（LIS问题），前$i$个且第$i$个可以选也可以不选（本题）

如果是两个串就是以上状态的排列组合

也可

这个状态的隐含含义是一定要选A串的第$i$个。然后注意这道题目的不同段可以挨在一起；那个$p$肯定不能枚举的，利用“决策集合只增多不减少”的trick优化

update 2024.6.25

我们前面发现需要枚举互相匹配的$A$末尾的一段与$B$末尾的一段的长度的时候，我们就要想到“饼干”这道题目排除等效冗余的优化方法，于是去考虑怎么样把这种枚举等效，很自然的一个想法就是直接认为分$k$组时，$A[i]$直接接在前面已经分好了的$k$组后面，但这就要求我们一定要选$A[i-1]$，于是就有了上面两种做法（上面第一种做法是显式地指出了是否选择$A[i]$，第二种做法是隐式地指出了是否选择$A[i]$）