亚特兰蒂斯

这里主要是对代码的解释

首先是对蓝书的简单做法的代码解释

我们把每一个节点看做比较独立的一个个体，他的cnt表示他所代表的区间是否在他本身的影响下被完全覆盖，这里不太好描述，下面举一个例子

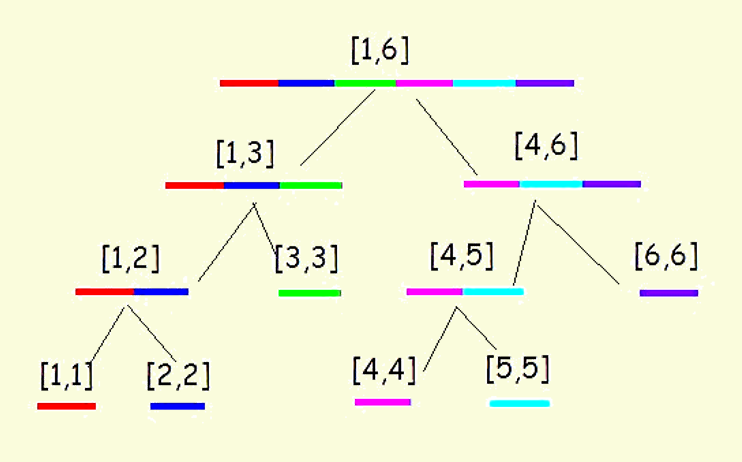
比如三号节点（代表区间为[4,6]）的cnt>0表示这一段区间在他这里已经被完全覆盖了，cnt=0表示在他这里没有被完全覆盖

那么在实际中，一个单位区间如何判断他是否被覆盖？

就看从代表这个区间的叶子节点到根节点的路径上，是否存在一个节点的cnt>0

比如[4,4]这个区间，如果1,3,6,12这四个节点中有一个cnt>0那么就代表实际中，[4,4]这个区间被覆盖了

我们先不考虑长度，先单独考虑维护区间是否被覆盖，那么在这种情况下，当修改操作为+1时，线段树被划分成的若干个节点的cnt都加上1，从每一个叶子节点往上走，显然都是符合实际情况的，如果修改操作为-1，当线段树被划分成的若干个节点中的某一个节点的cnt变为0了，他所代表的这些单位区间往上走，如果某个单位区间在实际中还被覆盖，那么他一定是被之前的某一次+1操作在路径上的另一个节点覆盖的，由于操作成对出现，这个节点的-1操作肯定比+1操作后面出现，所以这个节点的cnt一定>0，所以也就不会遗漏答案，同样的分析，也不会重复计算

我们再来考虑长度，由于线段树是从下往上维护信息的，我们不妨用最暴力的方法来维护信息，假设每次修改完了之后我们都从每个单位区间向上走，走到某一个节点时，如果当前节点的cnt=0，就向上传递其子节点的len之和，如果cnt>0就传递这个区间长度，那么由我们以上分析，如果一个单位区间被记录了，那么他一定会在某一个节点（cnt>0）的时候被计算贡献，也就不会遗漏答案（这个时候其实线段树中除了根节点外的节点的len可能不是实际中的len，但是由于我们只关心根节点，根节点的len一定是实际的len，就无所谓）

我们在修改之后可以直接模拟这个过程，在某次修改中，没有被涉及的区间显然不用管，他们已经传递好了，对于涉及的区间，如果cnt被减为了0，那么我们假设从这个区间所代表的的所有单位区间向上走，由于这个区间的子树都没有被修改，所以我们不用真的走，这个区间的两个子节点的len值就是已经走完之后的len，我们直接上传两个子节点的len即可

然后我们考虑如果硬要用lazy标记怎么做

首先我们考虑简单一点的情况，我们先不管区间长度，我们只维护$c$数组

相当于就是简单的区间修改，区间查询最小值

t[p].dat表示$p$这个节点所代表区间的$c$的最小值，t[p].lazy表示$p$这个节点的lazy标记（自己已经改变了，但是子节点的dat和lazy还需要加上自己这个lazy的变化）

根据我们对lazy的理解，在任何一个时刻，某一个节点的dat可能不是真正的dat，必须要加上从这个节点到根节点的路径上所有节点的lazy值之和才是真正的dat；在修改函数或者查询函数走到某一个节点时，这个节点的dat和lazy是真实的

想一下我们的问题出现在哪里，如果我们现在要维护不为$0$的$c$的长度总和，就要增加一个维度，t[p].len表示$p$这个节点所代表的的区间的真实长度和（注意，lazy是管dat的，就是说只有dat的值才可能不是真实的，我们不放认为在任意时刻，len的值都是真实的，下文尝试维护这个真实性）

那么我们在修改的时候，如果t[p].dat从$1$减到了$0$，我们要怎么修改t[p].len呢？也许我们会认为有t[p].len=t[leftson].len+t[rightson].len，但实际上这是错误的，根据我们对lazy标记的理解，此时leftson和rightson的dat值并不是真实的（因为修改函数没有继续往下面递归了），也许我们会说，肯定都为$0$啊，的确，但是len呢？两者的len也是错误的。为什么？因为p的dat为$0$，则说明$p$所代表的区间的某些$c$变成了$0$，然而此时你的leftson和rightson的len却是两者的区间长度（因为两者的dat不为$0$），所以肯定不是t[p].len=t[leftson].len+t[rightson].len

上文的分析也说明了我们要修改t[p].len就要先修改$p$的左右儿子的len，然而我们在修改左右儿子的len时，要先修改左右儿子的左右儿子的len，然后以此类推，肯定超时

所以我们必须换一个思路，我们认为t[p].len表示$p$所代表的的区间的所有$c$的值为dat的$c$的长度和，比如

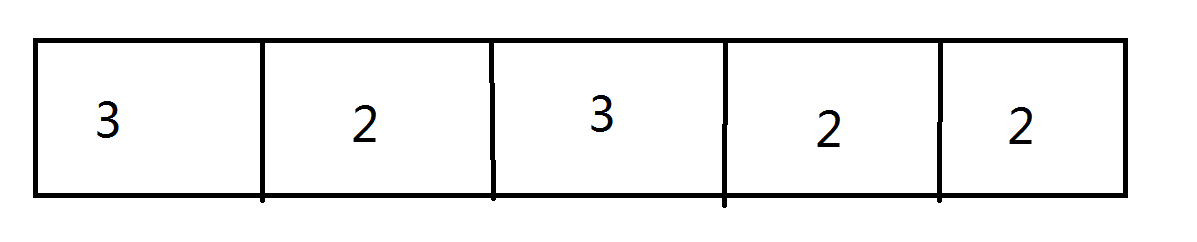
显然dat是2，那么为2的长度和为3，所以len就为3

如果任意时刻任意节点的len都是真实的，那么当我们递归到$p$这一个节点（$p$被完全覆盖，不会继续往下递归）的时候，t[p].len显然不变（而且$p$子树的所有节点的len都不变），我们只需要考虑如何改变$p$的父亲的len

假设我们现在回溯了到$p$的父亲了（我们假设已经走完了这个父亲的两个子节点，而且两个子节点的数据都已经维护好了），那么我们只需要判断这个父亲的dat（注意，此时这个dat是真实的）与两个儿子哪个的dat相同，那么父亲的len就是这个儿子的len（当然可能与两个都相同，这个时候父亲的len就是两个儿子的len的和）

由数学归纳法，我们可以知道我们维护的操作是正确的

update 2024.5.18

其实蓝书的做法就是标记永久化，观察目前所用到的标记永久化的题目（这道题目，李超线段树，蒟蒻的数列），就会发现线段树的节点代表的都不是真实值，要么是单点查询（此时可以累积路径上所有标记的影响），要么是与根节点有关的查询

update 2024.7.30

其实我们对lazy标记的理解又更深了一层，除了叶子节点，我们可以知道任意一个节点维护的量代表什么：代表不考虑从这个节点到根节点路径上所有节点的lazy值（也就是忽略这些操作）所得到的值，这个值如果考虑了从这个节点到根节点路径上所有节点的lazy值就会变成当前最新的真实值

我们再来严格证明一下为什么蓝书的做法（指的是维护$c$数组，然后答案就是书上说的这么累加）是对的

如果两条线段之间，扫描线上某个单位线段被覆盖了，这就说明一定存在一个矩形，其左边界在扫描线左边，右边界在扫描线右端，也就是说这个单位线段扫描的这个区域，至少会被这个矩形覆盖，也就不会多统计；如果两条线段之间，扫描线上某个单位线段没被覆盖，那么这个单位线段扫描的这个区域不可能是面积并的一部分，如果是的话，肯定有一个矩阵满足其左边界在扫描线左边，右边界在扫描线右端，这个单位线段也就不会不被覆盖了