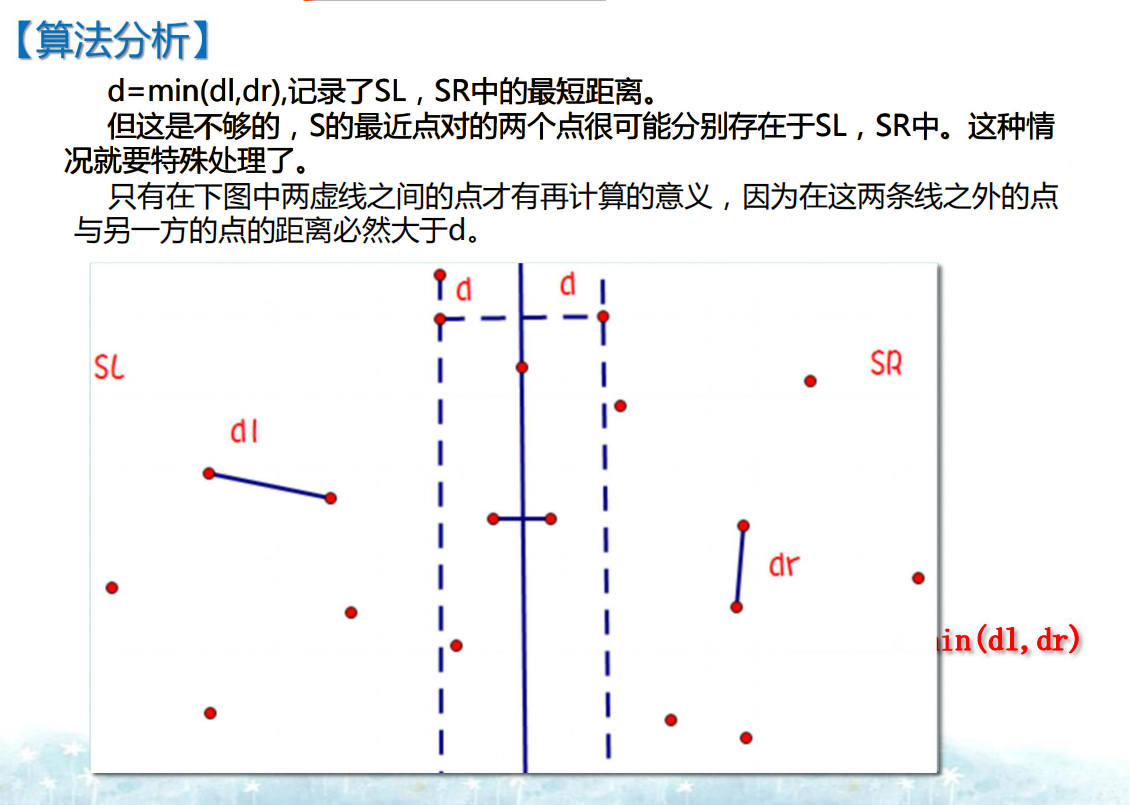
平面最近点对

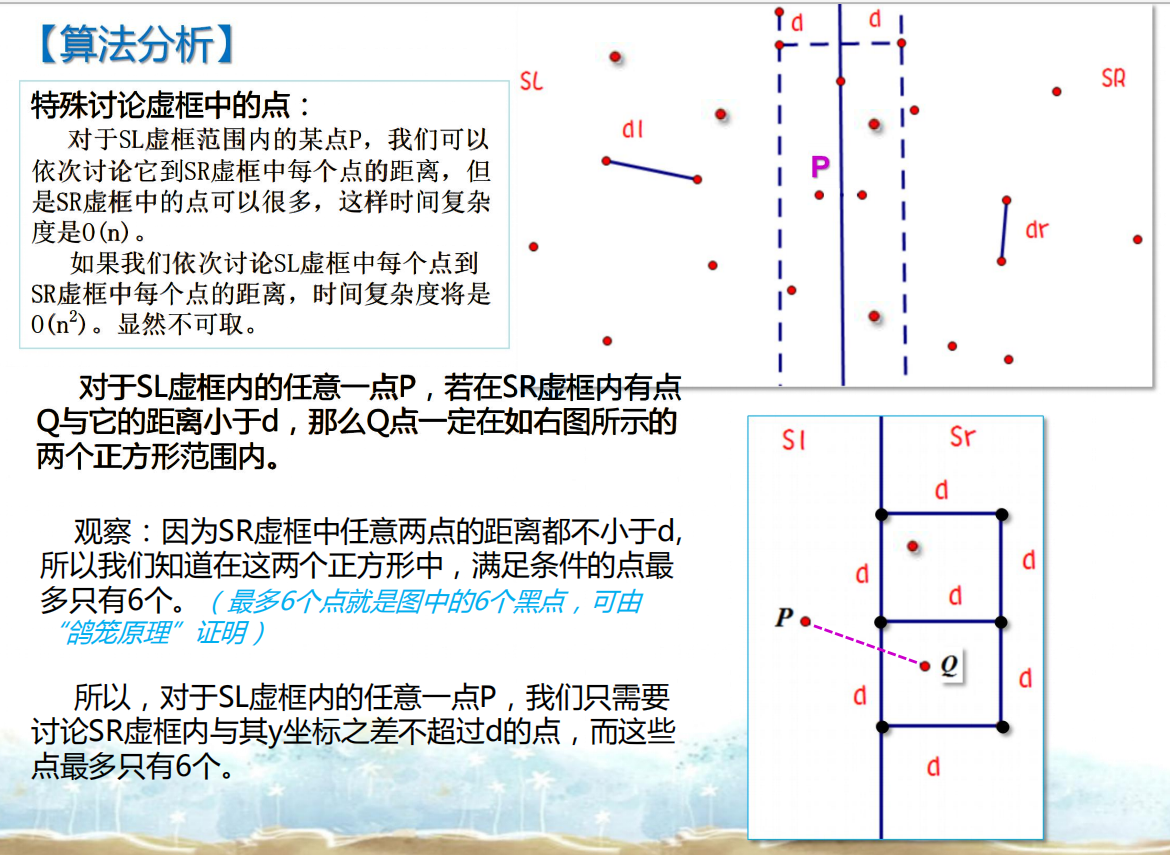
先证明这个最多6个

我们将\(d \times 2d\)的长方形划分成6个\(\frac{1}{2}d \times \frac{2}{3}d\)的小长方形，根据抽屉原理，如果大于6个点，那么至少有两个点在同一个小长方形里面，然而小长方形里面的距离最长是体对角线\(\frac{5}{6}d\)，所以矛盾，于是原结论正确

当然实际上，根据下面的代码，由于我们是将\(SL\)与\(SR\)的点放在同一个数组中，我们不应该将\(d \times 2d\)的长方形竖着放，而是应该横着放，并且跨越\(x=mid\)这条线

以上算法的时间复杂度是\(O(nlog^2n)\)，因为最多分成\(logn\)层，每一层点的总数是\(n\)，但是加上排序就会带上log

所以瓶颈是排序，我们想办法消除掉这个排序

一旦有了分治+排序，我们就可以想到利用归并排序的思想来消除复杂度

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=4e5+10;
int n;
struct Node
{
	ll x,y;
}temp[N],w[N];
int read()
{
    int x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-f;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-48;s=getchar();}
    return x*f;
}
bool cmp(Node i,Node j)
{
	return i.x<j.x;
}
ll dis(Node i,Node j)
{
	return (i.x-j.x)*(i.x-j.x)+(i.y-j.y)*(i.y-j.y);
}
ll cal(int l,int r)
{
	if(l==r) return 1e16;
	int mid=l+r>>1,cnt=0;
	ll Midx=w[mid].x;
	ll d=min(cal(l,mid),cal(mid+1,r));
	int i=l,j=mid+1;
	while(i<=mid||j<=r)//也可以用for循环写，这里只是写的像传统的归并排序罢了
	{
		while(i<=mid&&(ll)abs(w[i].x-Midx)*abs(w[i].x-Midx)>=d)//先筛选出在虚线框中的点 
		i++;
		while(j<=r&&(ll)abs(w[j].x-Midx)*abs(w[j].x-Midx)>=d) 
		j++;
		if(i<=mid)
		{
			if(j<=r)
			{
				if(w[i].y<w[j].y) temp[++cnt]=w[i++];//仍然按照y坐标升序
				else temp[++cnt]=w[j++];
			}
			else temp[++cnt]=w[i++];
		}
		else if(j<=r) temp[++cnt]=w[j++];
	}
	for(int i=1;i<cnt;i++)
	for(int j=i+1;j<=cnt&&(temp[j].y-temp[i].y)*(temp[j].y-temp[i].y)<d;j++)//最多只有6个点
	d=min(d,dis(temp[i],temp[j]));
	i=l,j=mid+1;
	int k=l;
	while(i<=mid&&j<=r)//归并排序
	{
		if(w[i].y<w[j].y) temp[k++]=w[i++];
		else temp[k++]=w[j++];
	}
	while(i<=mid) temp[k++]=w[i++];
	while(j<=r) temp[k++]=w[j++];
	for(int i=l;i<=r;i++)
	w[i]=temp[i];
	return d;
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++)
	w[i].x=read(),w[i].y=read();
	sort(w+1,w+n+1,cmp);
	printf("%lld",cal(1,n));
    return 0;
}

仍然按x排序，只不过\(d \times 2d\)的长方形变成了\(d\times 2d \times 2d\)的立方体，我们划分成32个\(\frac{d}{2} \times \frac{d}{2} \times \frac{d}{2}\)的小立方体，可知最多不超过32个点

当然有更优的划分，我们设划分为\(\frac{d}{a} \times \frac{d}{b} \times \frac{d}{b}\)，需要满足对角线长度（平方）\(\frac{1}{a^2}+\frac{2}{b^2}≤1\)，我们最终的目的是最小化\(\frac{4}{\frac{1}{ab^2}}=4ab^2\)，当\(a\)确定的时候，\(b\)肯定越小越好，也就有\(\frac{2}{b^2}=1-\frac{1}{a^2}\)，所以\(b^2=\frac{2a^2}{a^2-1}\)，所以\(4ab^2=\frac{8a^3}{a^2-1}\)，求导之后会发现极小值为\(12\sqrt3\)，大约是\(22\)个左右，不会比这个更小了

update 2024.7.14

求三维的最近点对，最后为什么一定是\(\frac{d}{a} \times \frac{d}{b} \times \frac{d}{b}\)而不是\(\frac{d}{a} \times \frac{d}{b} \times \frac{d}{c}\)呢？不太清楚自己当时怎么想的（只不过后者算出来也是\(12\sqrt3\)）