洛谷T200187

考虑走了\(x\)步向左，\(x+n\)步向右。容易知道最后一步一定会到达\(n\)，但是中间可能会提前到达\(n\)，我们需要去重。
我们使用卡特兰数的折线法去重。
以下令向左走一次变为向右上走一次，向右走一次变为向右下走一次（注意这里定义的转换，下文会多次用到），最终会走到点\((2x+n,-n)\)。如下图，是一种合法的方案（假设\(n=2\)）：LRRLRR。

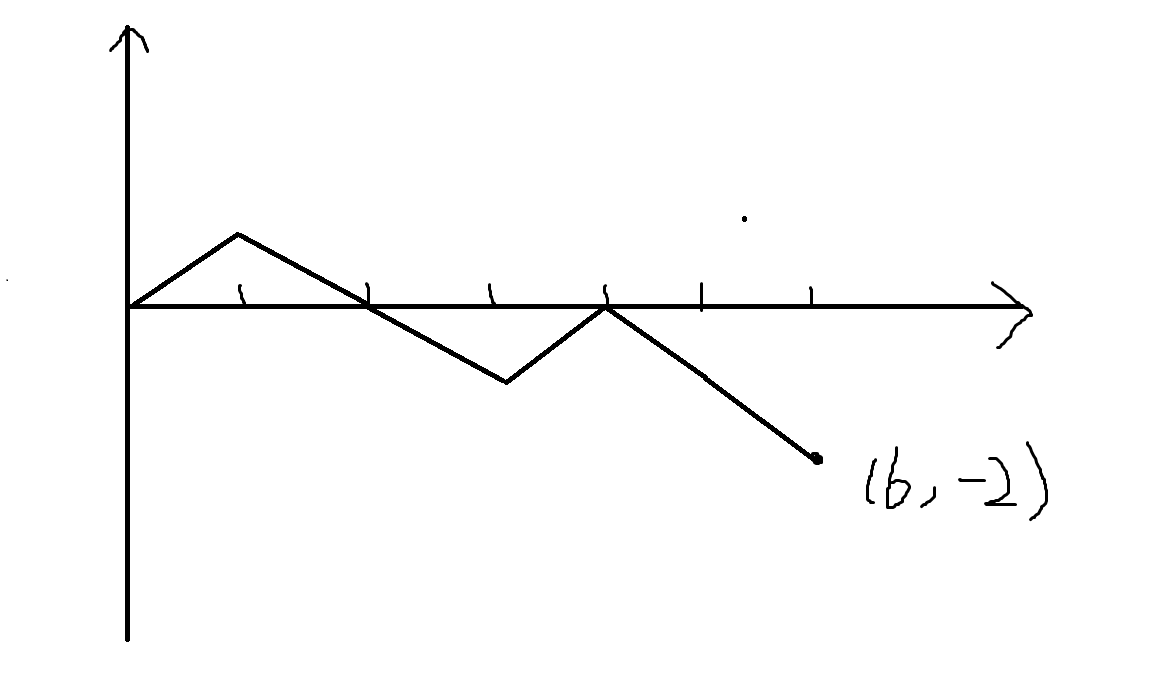
显然合法的方案一定不能在\(6\)之前碰到\(y=-2\)这条线。
所以合法的方案一定是从\((5,-1)\)向右边走一步后到达，不可能从\((5,-3)\)向左走一步到达（再次提醒，这里的向左/右走一步的定义已经改变，见上文，下文不再提醒）。
问题转化为从\((0,0)\)走到\((5,-1)\)，不超过\(y=-1\)这条线有多少种合法的方案数。
到这里已经跟卡特兰数的折线法很像了,可以自己思考了，不在举例。
首先总的方案数为\(\dbinom{2x+n-1}{x}\)（这代表组合数，下同）
对任意一种不合法的方案数，在第一次超过规定线的地方停止，将后面翻转，得到的方案数为\(\dbinom{2x+n-1}{x-1}\)
两者相减即可，乘上概率。
代码如下，注意如何实现\(O(n)\)得到多个数的逆元。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod=998244353;
const int N=1e7+10;
int read()
{
    int x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-f;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-48;s=getchar();}
    return x*f;
}
ll n,m,a,b;
ll jc[N],inv[N],inv1[N];
ll quickpow(ll a,ll b,ll c)
{
	ll res=1;
	a%=c;
	while(b)
	{
		if(b&1) res=(res*a)%c;
		a=(a*a)%c;
		b>>=1;
	}
	return res;
}
ll C(ll n,ll m)
{
	if(n<m||m<0) return 0;
	if(!m) return 1;
	return jc[n]*inv[m]%mod*inv[n-m]%mod;
}
int main()
{
	n=read(),m=read(),a=read(),b=read();
	jc[0]=1;
	for(int i=1;i<=m;i++) jc[i]=(jc[i-1]*i)%mod;
	inv[m]=quickpow(jc[m],mod-2,mod);
	for(int i=m;i>=1;i--) inv[i-1]=(inv[i]*i)%mod;
	ll pc=1;
	for(int i=1;i<=m;i++) pc=(pc*(a+b))%mod;
	inv1[m]=quickpow(pc,mod-2,mod);
	for(int i=m;i>=1;i--) inv1[i-1]=(inv1[i]*(a+b))%mod;
	ll ans=0;
	for(ll i=0,pa=1,pb=quickpow(b,n,mod);(i<<1)+n<=m;i++)
	{
		ans=(ans+((pa*pb%mod)*inv1[(i<<1)+n]%mod)*(C((i<<1)+n-1,i)-C((i<<1)+n-1,i-1)+mod)%mod)%mod;
		pa=(pa*a)%mod;
		pb=(pb*b)%mod;
	}
	printf("%lld",ans);
	return 0;
}