排序算法总结

1、排序算法稳定性

稳定性的概念远没有这么复杂，它只表示两个值相同的元素在排序前后是否有位置变化。如果前后位置变化，则排序算法是不稳定的，否则是稳定的。稳定性的定义符合常理，两个值相同的元素无需再次交换位置，交换位置是做了一次无用功。主要看是否有等于=。

为什么排序算法最差情况时间复杂度是O(N^2)：

pivot选择是在总是在第一个位置，T(N) = T （N -  1） + T （0） + O(N);

排序算法稳定性

排序法	平均时间	最差情形	稳定度	额外空间	备注
冒泡	O(n2)	O(n2)	稳定	O(1)	n小时较好
交换	O(n2)	O(n2)	不稳定	O(1)	n小时较好
选择	O(n2)	O(n2)	不稳定	O(1)	n小时较好
插入	O(n2)	O(n2)	稳定	O(1)	大部分已排序时较好
基数	O(logRB)	O(logRB)	稳定	O(n)	B是真数(0-9)， R是基数(个十百)
Shell	O(nlogn)	O(ns) 1<s<2	不稳定	O(1)	s是所选分组
快速	O(nlogn)	O(n2)	不稳定	O(nlogn)	n大时较好
归并	O(nlogn)	O(nlogn)	稳定	O(1)	n大时较好
堆	O(nlogn)	O(nlogn)	不稳定	O(1)	n大时较好

2、堆排序介绍

二叉树：

层数从0开始，那么第i层最多有 2^i 个节点，如果二叉树深度为k，那么总节点数为2 ^ (k + 1) - 1，最底层的节点数n2,其他层节点数为n0，那么n2 = n0 + 1;

堆：

使用的是完全二叉树，对应于一个vector实现，有最大堆和最小堆。

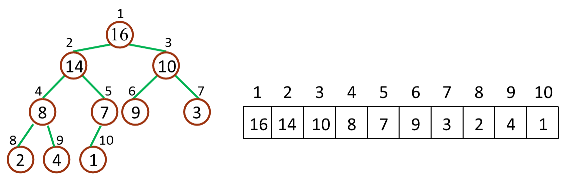
下标从1开始的话，对应关系是：

对于给定的某个结点的下标 i，可以很容易的计算出这个结点的父结点、孩子结点的下标：

• Parent(i) = floor(i/2)，i 的父节点下标
• Left(i) = 2i，i 的左子节点下标
• Right(i) = 2i + 1，i 的右子节点下标

下标从0开始的，对应关系是：

• Parent(i) = floor((i-1)/2)，i 的父节点下标
• Left(i) = 2i + 1，i 的左子节点下标
• Right(i) = 2i + 2，i 的右子节点下标

堆排序代码参考

#include<iostream>
#include<vector>
using namespace std;
//heapsort

void siftdown(vector<int> &vec, int i, int len) {
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    int largest = i;
    if (l < len && vec[l] > vec[i]) {
        largest = l;
    }
    if (r < len && vec[r] > vec[largest]) {//这里总是写成l，记住是比较后的largest
        largest = r;
    }
    if (largest != i) {
        swap(vec[i], vec[largest]);
        siftdown(vec, largest, len);//交换之后原来以i作为root，它的left和right都小于root，
                                    //满足要求，所以要递归到交换后的那个root，即largest
    }

}
void heapsort(vector<int> &vec) {
    if (vec.size() == 0) {
        return;
    }
    //创建一个最大堆
    for (int i = vec.size() / 2; i >= 0; --i) {//计算非叶子节点的过程中[0~len / 2]，就会顺便把后面排序。
        siftdown(vec, i, vec.size());
    }
    //堆排序
    for (int i = vec.size() - 1; i >= 0; --i) {
        swap(vec[0], vec[i]);
        siftdown(vec, 0, i);//这里的i不包括最后一个元素了，因为已经将最大元素交换到后面了
    }
}

 

//down to up
#include<iostream>
#include<vector>
using namespace std;
void siftdown(vector<int> &vec,int i,int sz) {
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    int largest = i;

    if (l < sz && vec[l] > vec[i]) {
        largest = l;
    }
    if (r < sz && vec[r] > vec[largest]) {
        largest = r;
    }
    if (largest != i) {
        swap(vec[i], vec[largest]);
        siftdown(vec, largest, sz);
    }

}
void heapsort(vector<int> &vec) {
    for (int i = vec.size() / 2; i >= 0; --i) {
        siftdown(vec, i, vec.size());
    }
    for (int i = vec.size() - 1; i >= 0;--i) {
        swap(vec[0], vec[i]);
        siftdown(vec, 0, i);//这里的i每次运行后最后一个元素就是不需要的，所以不需要i + 1;
    }
}
int main() {
    vector<int> vec{ 3,5,2,6,68,9 };
    heapsort(vec);
    for (int num : vec) {
        cout << num << " ";
    }
    system("pause");


}

 

归并思路：

1、序列一分为二；

2、子序列递归排序；

3、合并有序子序列。

必须要开一个暂存数组，保存中间排序元素。

#include<vector>
#include<iostream>
using namespace std;

void merge(vector<int>& vec, int lo, int mid, int hi) {	//这里是传入引用，才能每次修改

	vector<int> tempvec{vec};//每次拷贝vec注意点，如果写成tmpvec(vec.size(),0)则每次递归调用初始化这里就出错了，变为全为0，
                            //每一层递归调用都会开辟一个该递归层的tmp，而vec是传引用的形式，所以每层都一样
	int leftend = mid, rightend = hi;	
	int lpos=lo,rpos=mid+1;
        int temp=lo;

	while ((lpos <= leftend) && (rpos <=rightend )) {//compare two arrays,copy other numbers
		if (vec[lpos] <= vec[rpos])
			tempvec[temp++] = vec[lpos++];
		else
			tempvec[temp++] = vec[rpos++];
	}

	while (lpos <=leftend)
		tempvec[temp++] = vec[lpos++];
	
	while (rpos <= rightend )
		tempvec[temp++] = vec[rpos++];
	
	for (int iz = 0; iz <tempvec.size(); ++iz){
		vec[iz] = tempvec[iz];		
	}

}

void mergesort(vector<int>& vec, int lo, int hi) {//recursion
	int mid;	
	if ( lo < hi ) {//这里如果写相等的话会陷入死循环
		mid = (lo + hi) / 2;	//每步都执行完毕后再执行下一句，然后再倒着执行回来；	
		mergesort(vec, lo, mid);
		mergesort(vec, mid+1 , hi);
		merge(vec, lo, mid, hi);
	}
}

int main() {
	vector<int> vec{ 3,2,4,5,2 };
	int n = vec.size() - 1;	
	mergesort(vec, 0, n);
	for (int iz = 0; iz <=n; ++iz)
		cout<< vec[iz]<<" ";
	cout << endl;
	
}

快速排序：

 

#include<iostream>
#include<vector>
using namespace std;

int partition(vector<int>& seq, int lo, int hi) {//pivot右侧的都大，左侧的都小
	int rNum = lo + rand() % (hi - lo + 1);//找一个随机位置
	int pivot = seq[rNum];//先找锚点
	swap(seq[lo], seq[rNum]);

	while (lo < hi) {//左右交差进行查找
		/*先从右向左查找第一个小于pivot的元素*/
		while (lo < hi) {
			if (pivot < seq[hi])
				--hi;
			else
			{
				seq[lo] = seq[hi];
				++lo;
				break;
			}
		}
		/*从左向右查找第一个大于pivot的元素*/
		while (lo < hi) {
			if (pivot > seq[lo])
				++lo;
			else
			{
				seq[hi] = seq[lo];
				--hi;
				break;
			}
		}
	}
	seq[lo] = pivot;//记得将该点放到目的位置
	return lo;	
}
void quicksort(vector<int>& seq,int lo,int hi) {
	/*if (hi - lo < 1)*/
	if (hi < lo)
		return;
	int mid = partition(seq,lo,hi);
	quicksort(seq,lo,mid-1);
	quicksort(seq,mid+1,hi);
}


int main() {
	vector<int> seq{ 2,1,4,2,1 };
	quicksort(seq, 0, seq.size() - 1);
	for (unsigned int i = 0; i < seq.size(); ++i) 
		cout << seq[i] << " ";	
	cout << endl;
}