7专题总结-高频题high frequency
Outline 1. Single Number I, II, III 2. Majority Number I, II, III 3. Best Time to Buy and Sale Stock I, II, II 4. Subarray I, II, III, IV 5. 2-Sum, 3-Sum, 4-Sum, k-Sum, 3-Sum Closest 6. Partition Array 7. Quick Questions
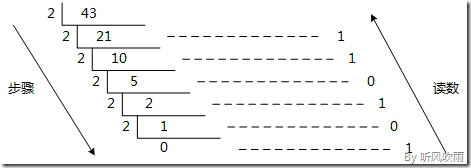
方法:除2取余法,即每次将整数部分除以2,余数为该位权上的数,而商继续除以2,余数又为上一个位权上的数,这个步骤一直持续下去,直到商为0为止,最后读数时候,从最后一个余数读起,一直到最前面的一个余数。
例:将十进制的(43)D转换为二进制的步骤如下:
1. 将商43除以2,商21余数为1;
2. 将商21除以2,商10余数为1;
3. 将商10除以2,商5余数为0;
4. 将商5除以2,商2余数为1;
5. 将商2除以2,商1余数为0;
6. 将商1除以2,商0余数为1;
7. 读数,因为最后一位是经过多次除以2才得到的,因此它是最高位,读数字从最后的余数向前读,101011,即(43)D=(101011)B。
(Figure:图解十进制 → 二进制)
思路:将所有数进行异或运算,异或运算是对应位相同则为0,不同则为1,相当于不进位加法,将所有数进行异或运算最后得到的就是不同的那个数。

class Solution { public: int singleNumber(vector<int>& nums) { if(nums.size() == 0){ return INT_MIN; } int result = 0; for(int i = 0;i < nums.size();++i){ result = result ^ nums[i]; } return result; } };
思路:也是利用第一题的思路,定义一个32位的数组,将所有数的特定一位进行统计,并对3取模,存入对应位里面,只有不同的那个数对应位才位1,内部循环结束后就得到最后结果对应位的1,然后二进制转化为十进制,将第几位进行转化就向左移动i位,记住这里的i是下标。不断加起来就可以得到结果。
bits[i] += (nums[j] >> i) & 1;//对应第i位进行统计,将十进制转化为二进制,想统计哪一位就除以i
bits[i] %= 3;
result += bits[i] << i;//二进制转化为十进制,将第几位进行转化就向左移动i位,记住这里的i是下标。

class Solution { public: int singleNumber(vector<int>& nums) { if(nums.size() == 0){ return -1; } int result = 0; vector<int> bits(32,0); for(int i = 0;i < 32;++i){ for(int j = 0;j < nums.size();++j){ bits[i] += (nums[j] >> i) & 1;//对应第i位进行统计,将十进制转化为二进制,想统计哪一位就除以i bits[i] %= 3; } result += bits[i] << i;//二进制转化为十进制,将第几位进行转化就向左移动i位,记住这里的i是下标。 } return result; } };
思路:使用异或运算找出那两个数。1)使用异或运算得到XOR;2)找到XOR中最后一位是1,得到的是肯定不同的那一位:int lastBit = XOR - (XOR & (XOR - 1));解释XOR - 1:
1xxxxxx1000 1xxxxxx1000
& 1xxxxxx0111 ==> - 1xxxxxx0000
--------------------------------- --------------------------------
1xxxxxx0000 10000
3)因为第一步中经过异或运算最后是两个不同的数left和right进行异或的,他们和lastbit进行与运算,就可以找出不同的那一位,将这两个数分开。然后两边分别异或运算就可以了。

class Solution { public: vector<int> singleNumber(vector<int>& nums) { if(nums.size() == 0){ return {}; } vector<int> result; int left = 0,right = 0; int XOR = 0; for(int i = 0;i < nums.size();++i){ XOR ^= nums[i]; } //find last bit equal to 1 int lastBit = XOR - (XOR & (XOR - 1)); for(int j = 0;j < nums.size();++j){ if(nums[j] & lastBit){ left ^= nums[j]; } else{ right ^= nums[j]; } } result.push_back(left); result.push_back(right); return result; } };
2.1 Majority Number
http://www.lintcode.com/en/problem/majority-number/
思路:定义一个count,一个candidate,没次选择一个进行抵消,因为最终的数肯定大于50%,所以最后的candidate一定就是结果。

class Solution { public: /** * @param nums: A list of integers * @return: The majority number */ int majorityNumber(vector<int> nums) { // write your code here if(nums.size() == 0){ return -1; } int count = 0,flag = -1; for(int i = 0;i < nums.size();++i){ if(count == 0){ flag = nums[i]; count = 1; } else{ if(flag == nums[i]){ ++count; } else{ --count; } } } return flag; } };
2.2 Majority Number II
http://www.lintcode.com/en/problem/majority-number-ii/
给定一个整型数组,找到主元素,它在数组中的出现次数严格大于数组元素个数的三分之一。
思路:注意if else的顺序很重要,只要判断了count1以及flag1是否和nums[i]相等,再按照同样的思路判断count2.不然就会出错,使得flag1和flag2相等。
与Majority Number 1相似。但我们要保存2个number.
1. 遇到第一个不同的值,先记录number 2.
2. 新值与n1,n2都不同,则cnt1,cnt2都减少
3. 当n1,n2任意一个为0时,从新值中挑出一个记录下来。
4. 最后再对2个候选值进行查验,得出最终的解。
主页君其实也想不太明白这个题目为什么这样解。
还是举个例子吧
7 1 7 7 61 61 61 10 10 10 61
n1 7 7 7 7 7 7 7 7 7 10 10
cnt1 1 1 2 3 2 2 2 1 0 1 1
n2 0 1 1 1 1 61 61 61 61 61 61
cnt2 0 1 1 1 0 1 2 1 0 0 1
证明:
1. 我们对cnt1,cnt2减数时,相当于丢弃了3个数字(当前数字,n1, n2)。也就是说,每一次丢弃数字,我们是丢弃3个不同的数字。
而Majority number超过了1/3所以它最后一定会留下来。
设定总数为N, majority number次数为m。丢弃的次数是x。则majority 被扔的次数是x
而m > N/3, N - 3x > 0.
3m > N, N > 3x 所以 3m > 3x, m > x 也就是说 m一定没有被扔完
最坏的情况,Majority number每次都被扔掉了,但它一定会在n1,n2中。
2. 为什么最后要再检查2个数字呢?因为数字的编排可以让majority 数被过度消耗,使其计数反而小于n2,或者等于n2.前面举的例子即是。
另一个例子:
1 1 1 1 2 3 2 3 4 4 4 这个 1就会被消耗过多,最后余下的反而比4少。

class Solution { public: /** * @param nums: A list of integers * @return: The majority number occurs more than 1/3. */ int majorityNumber(vector<int> nums) { // write your code here if(nums.size() == 0){ return -1; } int count1 = 0,count2 = 0; int flag1 = 0,flag2 = 0; for(int i = 0;i < nums.size();++i){ if(count1 == 0){ flag1 = nums[i]; count1 = 1; } else if(flag1 == nums[i]){ ++count1; } else if(count2 == 0){ flag2 = nums[i]; count2 = 1; } else if(flag2 == nums[i]){ ++count2; } else{ --count1; --count2; } } count1 = count2 = 0; for(int j = 0;j < nums.size();++j){ if(flag1 == nums[j]){ ++count1; } if(flag2 == nums[j]){ ++count2; } } return count1 > count2 ? flag1 : flag2; } };
2.3 Majority Number III
http://www.lintcode.com/en/problem/majority-number-iii/
给定一个整型数组,找到主元素,它在数组中的出现次数严格大于数组元素个数的1/k。
思路:思路和Majority NumberII 一样,维护k-1个candidate 在map里面,key为数字值,value为出现次数。先找到这k-1个candidate后,扫描所有元素,如果该元素存在在map里面,update map;如果不存在,1: 如果map里面有值为count= 0,那么删除掉这个元素,加入新元素;2:map里面没有0出现,那么就每个元素的count--
剩下的map里面的值都有可能是majority,所以重新扫描数组,记录下每一个元素出现次数,次数最大的就是majority
solution:http://www.jiuzhang.com/solution/majority-number-iii
3.1 121. Best Time to Buy and Sell Stock
https://leetcode.com/problems/best-time-to-buy-and-sell-stock/description/
思路:不断的用当前值减去前面的最小值。

class Solution { public: int maxProfit(vector<int>& prices) { if(prices.size() == 0){ return 0; } int minNum = INT_MAX,maxProfic = INT_MIN; for(int i = 0;i < prices.size();++i){ minNum = min(minNum,prices[i]); maxProfic = max(maxProfic,prices[i] - minNum); } if(maxProfic < 0){ return 0; } return maxProfic; } };
3.2 122. Best Time to Buy and Sell Stock II
思路:实质是 贪心法,只要后一天比前一天的价钱高,就卖出,不断的进行prices[i] - prices[i -1]的判断。
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/description/

class Solution { public: int maxProfit(vector<int>& prices) { if(prices.size() == 0){ return 0; } int profit = 0; for(int i = 1;i < prices.size();++i){ if(prices[i] > prices[i - 1]){ profit += (prices[i] - prices[i - 1]); } } return profit; } };
3.3 123. Best Time to Buy and Sell Stock III
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/description/
思路:
才意识到可以在整个区间的每一点切开,然后分别计算左子区间和右子区间的最大值,然后再用O(n)时间找到整个区间的最大值。
看来以后碰到与2相关的问题,一定要想想能不能用二分法来做!
下面复制参考的讲解,我觉得我不能比他讲的更好了
O(n^2)的算法很容易想到:
找寻一个点j,将原来的price[0..n-1]分割为price[0..j]和price[j..n-1],分别求两段的最大profit。
进行优化:
对于点j+1,求price[0..j+1]的最大profit时,很多工作是重复的,在求price[0..j]的最大profit中已经做过了。
类似于Best Time to Buy and Sell Stock,可以在O(1)的时间从price[0..j]推出price[0..j+1]的最大profit。
但是如何从price[j..n-1]推出price[j+1..n-1]?反过来思考,我们可以用O(1)的时间由price[j+1..n-1]推出price[j..n-1]。
最终算法:
数组l[i]记录了price[0..i]的最大profit,
数组r[i]记录了price[i..n]的最大profit。
已知l[i],求l[i+1]是简单的,同样已知r[i],求r[i-1]也很容易。
最后,我们再用O(n)的时间找出最大的l[i]+r[i],即为题目所求。

class Solution { public: int maxProfit(vector<int>& prices) { if(prices.size() == 0){ return 0; } int len = prices.size(); vector<int> left(len,0); vector<int> right(len,0); //left -> right int minNum = prices[0]; for(int i = 1;i < len;++i){ minNum = min(minNum,prices[i]); left[i] = max(left[i - 1],prices[i] - minNum); } //right -> left int maxNum = prices[len - 1]; for(int j = len - 2;j >= 0;--j){ maxNum = max(maxNum,prices[j]); right[j] = max(right[j + 1],maxNum - prices[j]); } //find maxprofit int maxProfit = 0; for(int k = 0;k < len;++k){ maxProfit = max(maxProfit,left[k] + right[k]); } return maxProfit; } };
3.4 188. Best Time to Buy and Sell Stock IV
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/description/
思路: Code Ganker ,Grandyang。
Code Ganker ,Grandyang。
使用动态规划求解,难点在于递推式。
一个是当前到达第i天可以最多进行j次交易,最好的利润是多少(global[i][j]),
另一个是当前到达第i天,最多可进行j次交易,并且最后一次交易在当天卖出的最好的利润是多少(local[i][j])。
global[i][j]=max(local[i][j],global[i-1][j]),依据是否包含最后一天的交易来分析,包含最后一天就是local[i][j]
local[i][j]=max(global[i-1][j-1]+max(diff,0),local[i-1][j]+diff),第一个是全局到i-1天进行j-1次交易,然后加上今天的交易,如果今天是赚钱的话(也就是前面只要j-1次交易,最后一次交易取当天),第二个量则是取local第i-1天j次交易,然后加上今天的差值(这里因为local[i-1][j]比如包含第i-1天卖出的交易,所以现在变成第i天卖出,并不会增加交易次数,而且这里无论diff是不是大于0都一定要加上,因为否则就不满足local[i][j]必须在最后一天卖出的条件了,也相当于将第i - 1天和第i天的交易合并在一起了)。
用II的解法优化k > prices.size / 2的情况,因为一次交易需要两个数据,最多只能prices.size() / 2交易

class Solution { public: int maxProfit(int k, vector<int>& prices) { if(prices.size() == 0) { return 0; } //用II的解法优化k > prices.size / 2的情况,因为一次交易需要两个数据,最多只能prices.size() / 2交易 if(k > prices.size() / 2){ int sum = 0; for(int i = 1; i < prices.size(); i++){ if(prices[i] > prices[i - 1]){ sum += prices[i] - prices[i - 1]; } } return sum; } //初始化全局变量和局部变量 vector<vector<int>> global(prices.size(),vector<int> (k + 1,0)); vector<vector<int>> local(prices.size(),vector<int> (k + 1,0)); for(int i = 1; i < prices.size(); i++){ int diff = prices[i] - prices[i - 1]; for(int j = 1; j < k + 1; j++){ //更新局部变量 local[i][j] = max(global[i - 1][j - 1] + max(0, diff), local[i - 1][j] + diff); //更新全局变量 global[i][j] = max(global[i - 1][j], local[i][j]); } } return global[prices.size() - 1][k]; } };
4.1 53. Maximum Subarray
https://leetcode.com/problems/maximum-subarray/description/
注意INT_MIN是计算机能表示的最小的数-2147483648,在减去一个数就变为正数2147483647。
思路:参考这是一道非常经典的动态规划的题目,用到的思路我们在别的动态规划题目中也很常用,以后我们称为”局部最优和全局最优解法“。
基本思路是这样的,在每一步,我们维护两个变量,一个是全局最优,就是到当前元素为止最优的解是,一个是局部最优,就是必须包含当前元素的最优的解。接下来说说动态规划的递推式(这是动态规划最重要的步骤,递归式出来了,基本上代码框架也就出来了)。假设我们已知第i步的global[i](全局最优)和local[i](局部最优),那么第i+1步的表达式是:
local[i+1]=Math.max(A[i], local[i]+A[i]),就是局部最优是一定要包含当前元素,所以不然就是上一步的局部最优local[i]+当前元素A[i](因为local[i]一定包含第i个元素,所以不违反条件),但是如果local[i]是负的,那么加上他就不如不需要的,所以不然就是直接用A[i];
global[i+1]=Math(local[i+1],global[i]),有了当前一步的局部最优,那么全局最优就是当前的局部最优或者还是原来的全局最优(所有情况都会被涵盖进来,因为最优的解如果不包含当前元素,那么前面会被维护在全局最优里面,如果包含当前元素,那么就是这个局部最优)。
接下来我们分析一下复杂度,时间上只需要扫描一次数组,所以时间复杂度是O(n)。空间上我们可以看出表达式中只需要用到上一步local[i]和global[i]就可以得到下一步的结果,所以我们在实现中可以用一个变量来迭代这个结果,不需要是一个数组,也就是如程序中实现的那样,所以空间复杂度是两个变量(local和global),即O(2)=O(1)。
技巧:local,global初始化的时候不要直接初始化为INT_MIN,这样计算的时候遇到负数就会出错,直接初始化为nums[0],然后循环从1开始。

class Solution { public: int maxSubArray(vector<int>& nums) { if(nums.size() == 0){ return 0; } int local = 0,global = 0; for(int i = 0;i < nums.size();++i){ local = max(nums[i],local + nums[i]);//必须包含当前元素 global = max(local,global);//包含当前元素和不包含当前元素的值选最大的 } return global; } };
4.2 minimum-subarray
http://www.lintcode.com/problem/minimum-subarray/
思路:上面那题将max 换成min就可以了。
4.3 maximum-subarray-difference
http://www.lintcode.com/problem/maximum-subarray-difference/
思路:使用四个数组,分别求出从左往右的最大值和最小值数组;在求出从右往左的最大值和最小值数组。
最后用一个循环将leftMax -rightMin,leftMin - rightMax;

class Solution { public: /** * @param nums: A list of integers * @return: An integer indicate the value of maximum difference between two * Subarrays */ int maxDiffSubArrays(vector<int> nums) { // write your code here if(nums.size() == 0){ return 0; } int len = nums.size(); vector<int> leftMax(len,0),leftMin(len,0); vector<int> rightMax(len,0),rightMin(len,0); //left => right find max int leftSum = nums[0]; leftMax[0] = nums[0]; for(int i = 1;i < len;++i){ leftSum = max(leftSum + nums[i],nums[i]); leftMax[i] = max(leftMax[i - 1],leftSum); } //right => left find max int rightSum = nums[len - 1]; rightMax[len - 1] = nums[len - 1]; for(int i = len - 2;i >= 0;--i){ rightSum = max(rightSum + nums[i],nums[i]); rightMax[i] = max(rightSum,rightMax[i + 1]); } //left => right find min int leftSum1 = nums[0]; leftMin[0] = nums[0]; for(int i = 1;i < len;++i){ leftSum1 = min(leftSum1 + nums[i],nums[i]); leftMin[i] = min(leftMin[i - 1],leftSum1); } //right => left find min int rightSum1 = nums[len - 1]; rightMin[len - 1] = nums[len - 1]; for(int i = len - 2;i >= 0;--i){ rightSum1 = min(rightSum1 + nums[i],nums[i]); rightMin[i] = min(rightSum1,rightMin[i + 1]); } //find maximum int result = INT_MIN; for(int i = 0;i < len - 1;++i){ int lMinRMax = abs(leftMin[i] - rightMax[i + 1]); int lMaxRMin = abs(leftMax[i] - rightMin[i + 1]); result = max(result,max(lMinRMax,lMaxRMin)); } return result; } };
4.4 subarray-sum-closest
http://www.lintcode.com/problem/subarray-sum-closest/
思路:参考
题目的意思是在一个数组中找一段连续的区间,使得这段区间的和的绝对值最小。做法就是利用前缀和,先用一个数组acc[i]来保存从nums[0]到nums[i]的和,同时还要记录下标,所以这里我用pair<int, int>来保存。那么,我们想要得到nums[i]到nums[j]的和,只要用acc[j] - acc[i-1]就可以了。但是这里有一点要注意要加一个辅助的节点,那就是[0, -1],这样就可以确保可以找到以nums[0]开始的区间了。剩下的工作就是对acc数组排序,找到排序后相邻的差的绝对值最小的那一对节点。