1专题总结—二分查找与旋转排序数组

  1、二分搜索的模板。

     算法面试中，如果需要优化O（n）的时间复杂度，那么只能是O（logn）的二分法。

     注意二分法大多数情况都是适用于排序数组。自己写二分的时候经常忘记写return -1；

http://www.lintcode.com/zh-cn/problem/first-position-of-target/

class Solution {
public:
    /**
     * @param nums: The integer array.
     * @param target: Target number to find.
     * @return: The first position of target. Position starts from 0. 
     */
    int binarySearch(vector<int> &array, int target) {
        // write your code here
        if(array.size()==0){
            return -1;
        }
        int start = 0,end = array.size() - 1;    
        while( start + 1 < end ){
            int mid = start + ( end - start ) / 2;
            if(array[mid]==target){
                end=mid;//找某个元素，直接return mid；找第一个元素end=mid;找last元素start=mid;
            }
            else if(array[mid]<target){
                start=mid;
            }
            else{
                end=mid;
            }
        }
        if(array[start]==target){
            return start;
        }
        else if(array[end]==target){
            return end;
        }
         return -1;
    }
};

模板有四点注意：

1）start+1<end;（最后会得到start，end两项）

2)mid=start+(end-start)/2;//为了防止start+end超出计算机表示范围

3)A[mid]==,<,>;

4)A[start]A[end]?target。（找第一个元素就是把A[start]放在前面，否则end放在if前面）

func binarySearch (nums []int, target int) int {
    // write your code here
    if len(nums) == 0 {
        return -1
    }
    start := 0
    end := len(nums) - 1
    for start + 1 < end {
        mid := start + (end - start) / 2
        if nums[mid] == target {
            end = mid
        }else if nums[mid] < target {
            start = mid
        } else {
            end = mid
        }
        
    }
    if nums[start] == target {
        return start
    }
    if nums[end] == target {
        return end
    }
    return -1
}

　　

2、使用二分搜索解决问题以及变种问题

找第一个位置&&找最后一个位置。

2.1搜索区间

http://www.lintcode.com/zh-cn/problem/search-for-a-range/

思路：使用二分搜索分别找到第一个等于target的元素和最后一个等于target的元素。(使用if判断一定要有对应的else，逻辑才会正确，不然会出错)

class Solution {
    /** 
     *@param A : an integer sorted array
     *@param target :  an integer to be inserted
     *return : a list of length 2, [index1, index2]
     */
public:
    vector<int> searchRange(vector<int> &A, int target) {
        // write your code here
        //find first target's position
        vector<int> result;
        if(A.size()==0)
            return {-1,-1};
        int start=0,end=A.size()-1;
        while(start+1<end){
            int mid=start+(end-start)/2;
            if(A[mid]==target){
                end=mid;
            }
            else if(A[mid]<target){
                start=mid;
            }
            else{
                end=mid;
            }                    
        }
        if(A[start]==target){
            result.push_back(start);
        }
        else if(A[end]==target){
            result.push_back(end);
        }
        else{
            result.push_back(-1);
        }
        
        //find last target's position        
        start=0;
        end=A.size()-1;
        while(start+1<end){
            int mid=start+(end-start)/2;
            if(A[mid]==target){
                start=mid;
            }
           else if(A[mid]<target){
                start=mid;
            }
            else{
                end=mid;
            }                    
        }
        if(A[end]==target){
            result.push_back(end);
        }
        else if(A[start]==target){
            result.push_back(start);
        }
        else{
            result.push_back(-1);
        }
        
    return result;    
    }
};

 2.2 查找插入位置Search Insert Position

https://leetcode.com/problems/search-insert-position/#/description

思路:使用模板二分法查找第一个大于插入元素的位置，需要注意的是当start和end都小于插入元素的时候，需要将元素插入到最后一个元素之后。

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        if(nums.size()==0){
            return -1;
        }
        int start=0,end=nums.size()-1;
        while(start+1<end){//找第一个大于target的位置
            int mid=start+(end-start)/2;
            if(nums[mid]==target){
                return mid;
            }
            else if(nums[mid]<target){
                start=mid;
            }
            else{
                end=mid;
            }
        }
       if(nums[start]>=target){
            return start;
        }
       else if(nums[end]>=target){
            return end;
        }
        else{
            return end+1;//这里没找到第一个大于的元素则插入到最后一个             //位置之后
        }
      
     return -1;  
    }
};            

二分法变式题

 2.3 Search a 2D Matrix.

https://leetcode.com/problems/search-a-2d-matrix/#/description

思路：因为整个二维数组是整体递增的，可以将二维数组看成一个一维递增数组，这就可以使用二分搜索，注意一维第k个元素和二维数组m*n的转化公式【k/n】【k%n】

注意：只要有除以n的地方，第一句一定要判断一下n是否为0.[[]];

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if(matrix.size()==0||matrix[0].size()==0){
            return false;
        }
        int m=matrix.size(),n=matrix[0].size();
        int totalNum=m*n-1;
        int start=0,end=totalNum;
         
        while(start+1<end){
            int mid=start+(end-start)/2;
            if(matrix[mid/n][mid%n]==target){
                return true;
            }
            else if(matrix[mid/n][mid%n]<target){
                start=mid;
            }
            else{
                end=mid;
            }
        }
        if(matrix[start/n][start%n]==target){
            return true;
        }
        else  if(matrix[end/n][end%n]==target){
            return true;
        }
        return false;
    }
};

2.4 Search a 2D Matrix II

https://leetcode.com/problems/search-a-2d-matrix-ii/#/description

思路：每个元素的左上角元素都小于该元素，每个元素的右下角元素都大于该元素。从矩阵的左下角开始搜索，如果m[i][j]==(直接返回),<（++j）,>(--i).

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        if(matrix.size()==0||matrix[0].size()==0){
            return false;
        }
        int row=matrix.size()-1,col=matrix[0].size()-1;
        int i=row,j=0;
        for( ; i>=0 && j<=col ; ){//i和j的条件同时满足用&&连接起来
            if(matrix[i][j]==target){
                return true;
            }
            else if(matrix[i][j]<target){
                    ++j;
            }
            else{
                --i;
            }
        }
        
        return false;
    }
    
};

2.5  First Bad Version

https://leetcode.com/problems/first-bad-version/#/description

思路：使用二分法找到第一个是false的bool值，二分法找first position。

注意：版本起始值是1，不要写成0，start=1！！！！注意接口返回如果是坏的版本返回的是true。

// Forward declaration of isBadVersion API.
bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
        if(n==0){
            return 0;
        }
        int start=1,end=n;
        while(start+1<end){
            int mid=start+(end-start)/2;
            if(isBadVersion(mid)){
                end=mid;
            }
            else if( ! isBadVersion(mid) ){
                start=mid;
            }
        }
        if(isBadVersion(start)){
            return start;
        }
        if(isBadVersion(end)){
            return end;
        }
        return 0;
    }
};

 2.6 Find Peak Element

https://leetcode.com/problems/find-peak-element/#/description

思路：本题思路就是使用二分法找到peak element。将每次二分元素所在位置划分为四种情况。 

1）nums[mid - 1] > nums[mid] && nums[mid] > nums[mid+1]下降阶段

2）nums[mid - 1] < nums[mid] && nums[mid] > nums[mid+1] 谷底

3）nums[mid - 1] < nums[mid] && nums[mid] < nums[mid+1]上升阶段

4）nums[mid - 1] < nums[mid] && nums[mid] > nums[mid+1]peak element

需要注意的是最后判断while结束之后。开始自己还判断一下start和end哪个是正确解，就是上面+1—1的方法，本题是肯定有解的，所以出来的start和end哪个大就选哪个最为最后的结果!!!!!!!!

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        if(nums.size()==0){
            return -1;
        }
        int start=0,end=nums.size()-1;//!!!!
        while(start+1<end){
            int mid=start+(end-start)/2;
            if(nums[mid+1]>nums[mid] && nums[mid]<nums[mid-1]){//谷底
                start=mid;
            }
            else if(nums[mid-1]>nums[mid] && nums[mid]>nums[mid+1]){//下降阶段
                end=mid;
            }
            else if(nums[mid+1]>nums[mid] && nums[mid]>nums[mid-1]){//上升阶段
                start=mid;
            }
            else if(nums[mid]>nums[mid-1] && nums[mid]>nums[mid+1]){
                return mid;
            }
        }
      if(nums[start]>nums[end]){
           return start;
       }
       else{
           return end;
       }
    }
        
};

3、旋转排序数组问题rotated sorted array

3.1 Find Minimum in Rotated Sorted Array

https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/#/description

无重复元素问题。

思路：使用二分法找到第一个小于最后一个元素的元素，注意最后退出循环对start和end的判断。

二刷注意：start + 1 < end，已经保证了至少有三个元素，两个元素不能进行while循环。所以该题不需要计算mid + 1 ，mid- 1是否在[0,size - 1] 这个范围内。

class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.size() == 0){
            return -1;
        }
        int start = 0,end =nums.size() - 1;
        int flag = nums[nums.size() - 1];
        while(start + 1 < end){
            int mid = start +(end - start)/2;
            if(nums[mid] < flag){
                end = mid;
            }
            else{
                start = mid;
            }
        }
        if(nums[start] < flag){
            return nums[start];
        }
       else {
            return nums[end];
        }
       
        return -1;
    }
};

3.2 Find Minimum in Rotated Sorted Array II

https://leetcode.com/problems/find-minimum-in-rotated-sorted-array-ii/#/description

有重复元素问题。

思路：使用二分搜索，nums[mid]元素和当前nums[end]做比较，如果大于end，则mid在上半段，否则在下半段。注意等于的时候要--end。

class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.size() == 0){
            return -1;
        }
        int start = 0,end = nums.size() - 1;
        while(start + 1 < end){
            int mid = start + (end - start) / 2;
            if(nums[mid] > nums[end]){
                start = mid;
            }
            else if(nums[mid] < nums[end]){
                end = mid;
            }
            else{
                --end;
            }
           
           
        }
       
        if(nums[start] > nums[end]){
            return nums[end];
        }
        else{
            return nums[start];
        }
    return -1;
    }
};

二刷思路：分为nums[0] 和nums[nums.size() - 1]。主要知道mid元素在上半部分还是下半部分，然后将相同的合并就可以得到答案。

class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.size()== 0){
            return -1;
        }
        int start = 0,end = nums.size() - 1;
        int endFlag = nums[end],startFlag = nums[0];
        while(start + 1 < end){
            int mid = start + (end - start) / 2;
            int sFlag = nums[0],eFlag = nums[end];
            if(sFlag != eFlag){
                if(nums[mid] <= eFlag){
                    end = mid;
                }
                else{
                    start = mid;
                }
            }
            else{
                if(nums[mid] < eFlag){
                    end = mid;
                }
                else if(nums[mid] > sFlag){
                    start = mid;
                }
                else{
                    --end;
                }
            }
        }
        if(nums[start] < nums[end]){
            return nums[start];
        }
        else{
            return nums[end];
        }
    }
};

3.3 Search in Rotated Sorted Array

https://leetcode.com/problems/search-in-rotated-sorted-array/#/description

思路：和3.2有点像，首先找到mid在上半段还是下半段，然后判断是在target是在上半段[start,mid]之间，还是下半段[mid,end]之间，或者这中间区域，判断条件里面一定要写清楚 if(target < nums[mid] && target > nums[0])这个条件，不然出错。

进一步思考：先考虑targe在哪个半段，分三种情况。在每种情况中，分别考虑mid所在位置，一定记得mid也要和last判断以及和target判断，全部情况先在纸上写出来，然后再合并同类项，就能写出很简洁的代码，写代码前一定要思考。

二刷：将target分为上半段和下半段分别考虑，在上半段的时候，只要 mid元素在下面就直接end = mid，下半段时同理可得。

class Solution {
public:
    int search(vector<int>& nums, int target) {
        if(nums.size() == 0){
            return -1;
        }
        int start = 0;
        int end = nums.size() - 1;
        int last = nums[end];
        while(start + 1 < end){
            int mid = start + (end - start)/2;
            if(nums[mid] == target){
                return mid;
            }
            if(target == nums[0]){
                return 0;
            }
             if(target == nums[end]){
                return end;
            }
            if(nums[mid] > last){//上半段
                if(target < nums[mid] && target > nums[0]){
                    end = mid;
                }
                else{
                    start = mid;
                }
            }
            else{
                if(target > nums[mid] && target <last){
                    start = mid;
                }
                else{
                    end = mid;
                }
            }
        }
        if(nums[start] == target){
            return start;
        }
        else if(nums[end] == target){
            return end;
        }
        return -1;
    }
};

 二刷代码：

class Solution {
public:
    int search(vector<int>& nums, int target) {
        if(nums.size() == 0){
            return -1;
        }
        int start = 0,end = nums.size() - 1;
        while(start + 1 < end){
            int mid = start + (end - start) / 2;
            int flag = nums[end];
            if(target > flag){
                if(nums[mid] <= flag){
                    end = mid;
                }
                else if(nums[mid] == target){
                    return mid;
                }
                else if(nums[mid] > target){
                    end = mid;
                }
                else{
                    start = mid;
                }
            }
            else if(target < flag){
                if(nums[mid] > flag){
                    start = mid;
                }
                else if(nums[mid] == target){
                    return mid;
                }
                else if(nums[mid] > target){
                    end = mid;
                }
                else{
                    start = mid;
                }
            }
            else{
                return nums.size() - 1;
            }
        }
        if(nums[start] == target){
            return start;
        }
        else if(nums[end] == target){
            return end;
        }
        return -1;
    }
};

 

3.4 Median of Two Sorted Arrays（比较难，爱考）

https://leetcode.com/problems/median-of-two-sorted-arrays/#/description

思路：运用递归加上二分搜索的方法，二分主要是每次将规模降低k/2的级别，比较A[k/2]和B[k/2]的大小，A[k/2]小的话，则result中前k/2个元素一定包含A[k/2]这k/2个元素。，这样每次就降低了规模。转化为找两个数组第k个数。

需要注意1）边界条件aStart >= nums1.size()则nums1中没有剩下的元素，转向nums2.

2）int aVal = aStart + k / 2 - 1 < nums1.size() ? nums1[aStart + k / 2 - 1]: INT_MAX;

这种方法很巧妙，避免判断aStart + k / 2 - 1大于nums1数组大小的时候，重新使用if进行判断的情况，直接赋值为无穷大，接下来判断的时候直接跳过a数组。

class Solution {
public:
    
   double findKth(vector<int>& nums1,int aStart,
                  vector<int>& nums2,int bStart,
                  int k){
        if(aStart >= nums1.size()){
            return nums2[bStart + k - 1];
        }
        if(bStart >= nums2.size()){
            return nums1[aStart + k - 1];
        }
        if(k == 1){
            return nums1[aStart] < nums2[bStart]
            ? nums1[aStart] : nums2[bStart]; 
        }
        
        int aVal = aStart + k / 2 - 1 < nums1.size() 
                   ? nums1[aStart + k / 2 - 1]
                   : INT_MAX;
        int bVal = bStart + k / 2 - 1< nums2.size() 
                   ? nums2[bStart + k / 2 - 1]
                   : INT_MAX;
        if(aVal < bVal){
            return findKth(nums1,aStart + k / 2, nums2,bStart,k - k / 2);
        }
        else{
            return findKth(nums1,aStart, nums2,bStart + k / 2,k - k / 2);
        }
       //return - 1;
   }
   
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int len = nums1.size() + nums2.size();
        double result = -1;
        if(len == 0){
            return result;
        }
        if(len % 2){
            result = findKth(nums1,0,nums2,0,len / 2 + 1);
        }
        else{
            // cout << findKth(nums1,0,nums2,0,len / 2 + 1);
            result = (findKth(nums1,0,nums2,0,len / 2) + findKth(nums1,0,nums2,0,len / 2 + 1)) / 2.0;
        }
        return result;
    }
};

二刷没做出来：每次只要对应k/2元素小于另外一个数组，则该部分一定在前k个元素中，如果担心k/2越界，就在首先就判断下标是否越界。

前面判断aStart是否小于a数组的大小，后面因为aStart + k / 2 - 1,所以也要判断是否越界，越界了就赋予无穷大，避免了很多if判断。递归基是k == 1的时候，递归每次都减少规模，将k / 2的元素增加到结果中，最终得到第k大的元素。

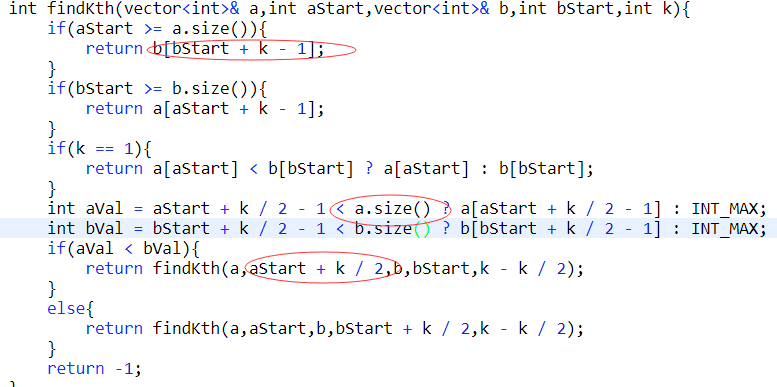
上面三点很容易出错，一定要注意。

 4、旋转类问题，比如字符串反转。

 使用三步反转法：

1）使用O（n）的时间，直接遍历找到反转的中间元素；

2）将中间元素前面的进行反转，再将后面的元素进行反转，这里需要使用交换操作比如swap的功能；

3）最后将整个数组进行反转。

4.1 Recover Rotated Sorted Array

http://www.lintcode.com/en/problem/recover-rotated-sorted-array/

思路：按照三步反转法的步骤进行就可以。注意开始是0 ~ idx - 1,然后是idx ~ end。

class Solution {
public:
    void swap_helper(vector<int> &nums, int start, int end) {
        for(start, end; start < end; ++start, --end) {
            swap(nums[start], nums[end]);
        }
    }
    void recoverRotatedSortedArray(vector<int> &nums) {
        // write your code here
        if(nums.size() < 2){
            return ;
        }
        int min_num = nums[0];
        int min_pos = 0;
        for(int i = 0;i < nums.size();++i){
            if(nums[i] < min_num){
                min_num = nums[i];
                min_pos = i;
            }
        }
        int end = nums.size() - 1;
        swap_helper(nums,0,min_pos - 1);
        swap_helper(nums,min_pos,end);
        swap_helper(nums,0,end);
    }
};

4.2Rotate String

http://www.lintcode.com/en/problem/rotate-string/

思路：记住string中一个元素是char类型。

二刷：offset = offset % str.size();因为可能大于数组大小，所以要取模。

class Solution {
public:
    /**
     * @param str: a string
     * @param offset: an integer
     * @return: nothing
     */
    void swap_helper(string &str,int start, int end){
        for(;start < end;++start,--end){
            char tmp;
            tmp = str[start];
            str[start] = str[end];
            str[end] = tmp;
            // swap(str[start],str[end]);
        }
        return;
    }
    void rotateString(string &str,int offset){
        //wirte your code here
        
        if(str.size() < 2  ){
            return;
        }
        offset = offset % str.size();
        if(offset == 0){
            return;
        }
        swap_helper(str,0,str.size() - 1);
        swap_helper(str,0,offset - 1);
        swap_helper(str,offset,str.size() - 1);
        return;
    }
};

4.3 翻转字符串

http://www.lintcode.com/zh-cn/problem/reverse-words-in-a-string/

思路：这题主要应该注意空格有多个的情况。使用istringstream将每个单词按照空格保存到一个string的vector中，然后将最后一个单词赋值给string，加上一个空格，依次类推可得到结果，注意string插入要使用push_back，或者append，如果使用insert（pos,num）,记得插入发生在pos的那个位置上。还有string这个字符串可以看成char的数组，string的插入必须是char的插入，不能插入string类型。

append必须是讲string接到后面。

如果输入有多个连续的空格，输出应该只有一个空格。判断的依据是istringstream输入的时候是以空格作为分界线的，多个空格输入的时候，通过这种方法读入string的时候是空的，所以后面判断no_space.size() == 0，就输出一个空格。

class Solution {
public:
    /**
     * @param s : A string
     * @return : A string
     */
    
  string reverseWords(string s) {
    // write your code here
    if (s.size() < 2) {
        return s;
    }
    istringstream ss(s);
    string tmp, result;
    vector<string> no_space;
    while (ss >> tmp) {
        no_space.push_back(tmp);
    }
    if(no_space.size() == 0){
        return " ";
    }
    int i;
    for (i = no_space.size() - 1; i > 0; --i) {
        result.append(no_space[i]);
        result.append(" ");
    }
    result.append(no_space[i]);
    return result;
}
};

 4.4 strStr

http://www.lintcode.com/en/problem/strstr/

思路：使用O(n^2)双重循环，注意定义变量前面要空一行，外层循环i<source.size() - target.size() + 1,这里很容易写错越界

指针为空就是指没有指向任何内容，*p = "";null

这道题二刷还是错：strlen:strlen的参数只能是char* 且必须是以'\0'结尾的.

class Solution {
public:
    /**
     * Returns a index to the first occurrence of target in source,
     * or -1  if target is not part of source.
     * @param source string to be scanned.
     * @param target string containing the sequence of characters to match.
     */
    int strStr1(string source, string target) {
        // write your code here
        if(source.size() == 0 && target.size() == 0){
            return 0;
        }
        // if(source.size() == 0 || target.size() == 0){
        //     return -1;
        // }
        int i, j;
        for(i = 0;i < source.size() - target.size() + 1;++i){
            for(j = 0;j < target.size();++j){
                if(source[j  + i] != target[j]){
                    break;
                }
            }
            if(j == target.size()){
                return i;
            }
        }
        return -1;
    }
    
     int strStr(const char *source, const char *target) {
        if (source == NULL || target == NULL) {
            return -1;
        }
        int target_size = strlen(target);
        int source_size = strlen(source);
        int i, j;
        for (i = 0; i < source_size - target_size + 1; i++) {
            for (j = 0; j < target_size; j++) {
                if (source[i + j] != target[j]) {
                    break;
                }
            }
            if (j == target_size) {
                return i;
            }
        }
        return -1;
    }

};