《图像处理》第9章 目标表示与描述
(仅个人学习摘抄)
9.1 概述
图像分割结果是得到了区域内的像素集合,或位于区域边界上的像素集合,这两个集合是的。
与分割类似,图像中的区域可用其内部(如组成区域的像素集合)表示,也可用其外部(如组成区域边界的像素集)表示。
一般来说,若果关心的是区域的反射性质,如灰度、颜色、纹理等,常用内部表示法;如果关心的是区域形状,则选用外部表示法。
1、表达:直接具体地表示目标
(1)内部表达:反射性质(灰度、颜色、纹理)
(2)外部表达:形状
好的表达方法应具有节省存储空间、易于特征计算等优点。
2、描述:抽象的表示目标
(1)用一组符号(描述子)来表征图像中被描述物体的某些特征,可以是对图像中各组成部分的性质的描述,也可以是各部分彼此间的关系的描述
(2)边界描述和区域描述
好的描述应在尽可能区别不同目标的基础上对目标的尺度、平移、旋转等不敏感,具有通用性。
3、关系
(1)表达对描述起重要作用,限定了描述的精确性
(2)只有目标的描述,表达方法才有意义
(3)表达侧重于数据结构,描述侧重于区域特征及区域间的联系和差别
9.2 表示方法
9.2.1 链码
链码用于表示由顺序连接的具有指定长度和方向的直线段组成的边界线。
这种表示方法基于线段的 4 或 8 连接,每一段的方向使用数字编号方法进行编码。
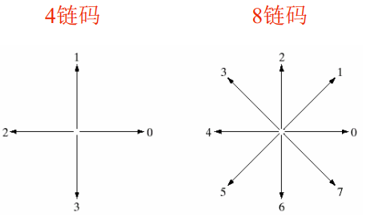

1、链码算法:
给每一个线段边界一个方向编码;有4链码和8链码两种编码方法。
从起点开始,沿边界编码,至起点被重新碰到,结束一个对象的编码。
2、缺点及改进:
(1)链码相当长;噪音会产生不必要的链码
改进:加大网格空间;依据原始边界与结果的接近程度,来确定新点的位置。
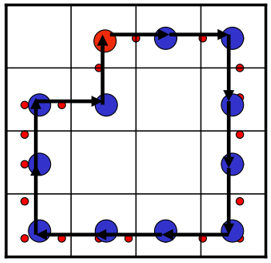
4-链码:003332221101
减少点的个数,降低链码长度。
(2)由于起点的不同,造成编码的不同
改进:从固定位置作为起点(最左最上)开始编码;起点归一化

(3)由于角度的不同,造成编码的不同
改进:通过使用链码的差分代替码字本身的方式
循环差分链码:用相邻链码的差分代替链码
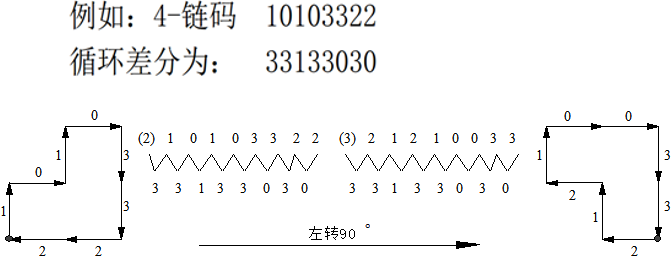
3、链码平滑
将原始的链码序列用较简单的序列代替
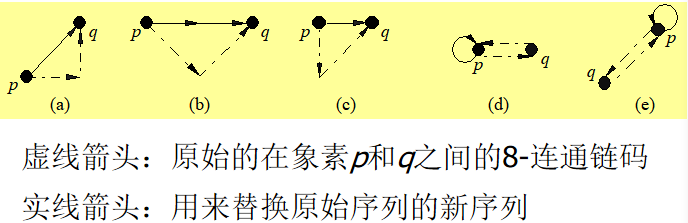
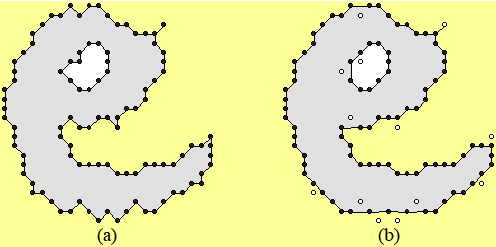
示例:
空心圆:平滑后被除去的原轮廓点
4、边界段和凸包
把边界分解成若干段分别表示;节省表达数据量;借助凸包(包含目标的最小凸形)概念。
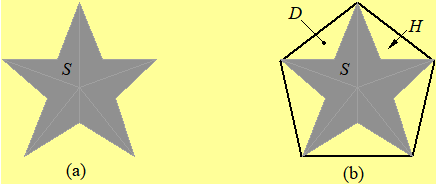
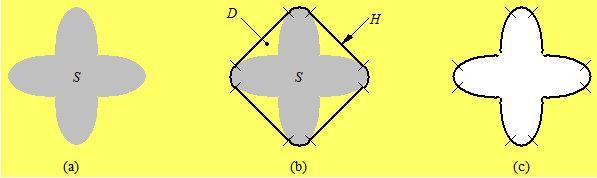
根据凸包把边界分解:
目标:像素集合 S
凸包:包含 S 的最小凸形 H
凸残差:D=H-S
9.2.2 多边形近似
基本思想:用最少的多边形线段,获取边界形状的本质。
寻找最小基本多边形的方法一般有两种:点合成法、边分裂法。
1、点合成算法
步骤:
(1)沿着边界选两个相邻的点对,计算首尾连接直线段与原始折线段的误差 R。
(2)如果误差 R 小于预先设置的阈值 T。去掉中间点,选新点对下一相邻点对,重复(1);否则,存储线段的参数,置误差为 0,选被存储线段的终点为起点,重复(1)(2)。
(3)当程序的第一个起点被遇到,算法结束。
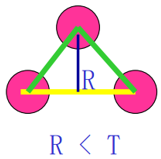
绿色是原本的边界,,当 R < T 时,上面那个点被去除。
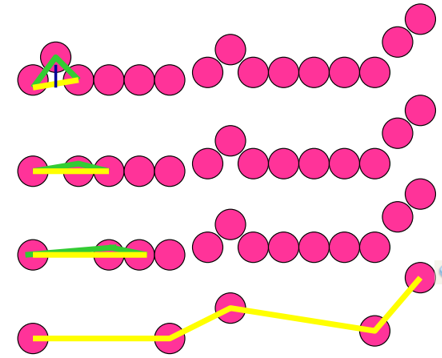
缺点:
顶点一般不对应于边界的拐点(如拐角)。因为新的线段直到超过误差的阈值才开始画。
2、分裂边算法
步骤:
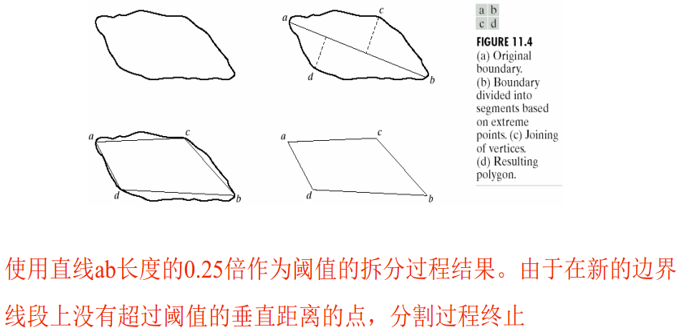
(1)连接边界线段的两个端点(如果是封闭边界,连接最远点);
(2)如果最大正交距离大于阈值,将边界分为两段,最大值点定位一个顶点。重复(1);
(3)如果没有超过阈值的正交距离,结束。
9.2.3 外形特征
1、基本思想
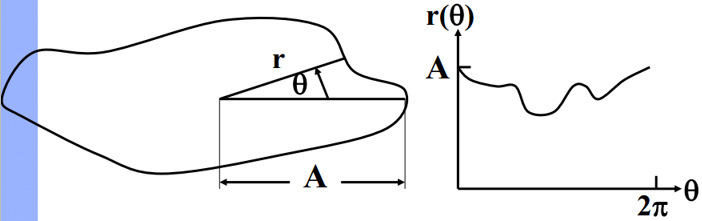
外形特征是一种用一维函数表达边界的方法。基本思想是把边界的表示降到一维函数。
2、函数定义
质心角函数:边上的点到质心的距离 r,作为夹角 θ 的函数 r(θ)。
3、缺点与改进
问题:函数依赖于旋转和比例缩放变换
改进:
(1)对于旋转——两种改进
① 选择离质心最远的点作为起点
② 选择从质心到主轴最远的点作为起点
(2)对于比例变换
对函数进行正则化,使函数值总是分布在相同的值域里,比如说 [0,1]。
9.3 边界描述子
9.3.1 简单描述子
边界的周长:最简单的描述符之一。沿轮廓线计算像素的个数,给出了一个长度的近似估计。
边界的直径:边界 B 的直径是
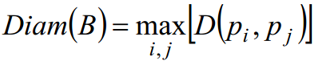
D 是欧氏距离或几何距离,pi,pj 是边界上的点。直径的长度和直径的两个端点连线(这条线被称为边界的主轴)的方向,是关于边界的有用的描述符。
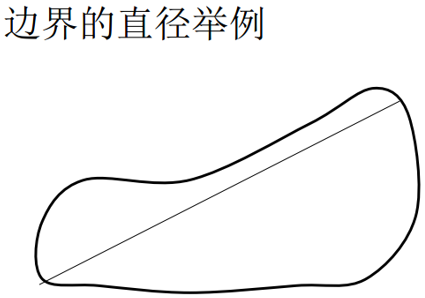
边界的曲率
曲率被描述为斜率的变化率。近似:用相邻边界线段(描述为直线)的斜率差作为在边界线交点处的曲率描述子。
交点 a 处的曲率为:dk = k1 - k2,其中 k1,k2 为相邻线段的斜率。
9.3.2 形状数
基于链码的一种边界形状描述。
轮廓差分码中其值最小的 1 个序列。

形状数定义:最小循环首差链码

形状数序号 n 的定义:形状数表达形式中的位数。上例序数为 8。对于封闭边界序号一定是偶数,如 4、6、8。
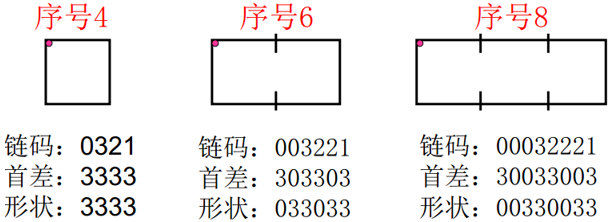
形状数与方向无关。
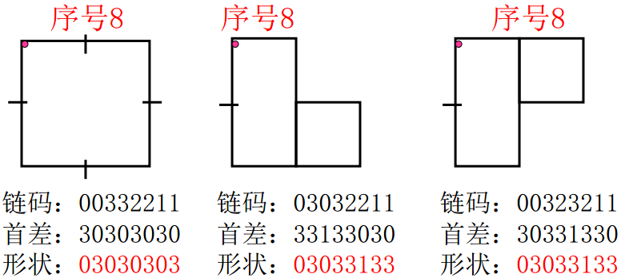
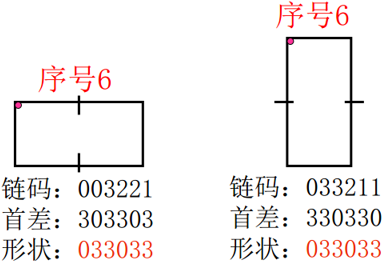
问题:虽然链码的首差是不依赖于旋转的,但一般情况下边界的编码依赖于网格的方向。
改进:规整化网格方向
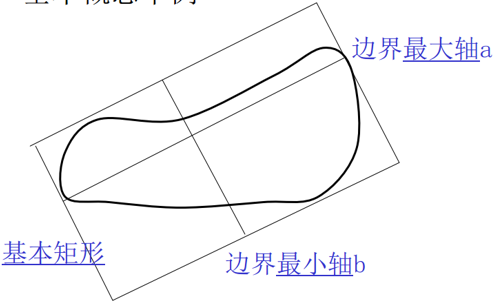
几个基本概念:
边界最大轴 a:是连接距离最远的两个点的线段。
边界最小轴 b:与最大轴垂直,且其长度确定的包围盒刚好包围边界。
边界离心率 c:最大轴长度与最小轴长度的比 c = a / b
基本矩形:包围边界的矩形。
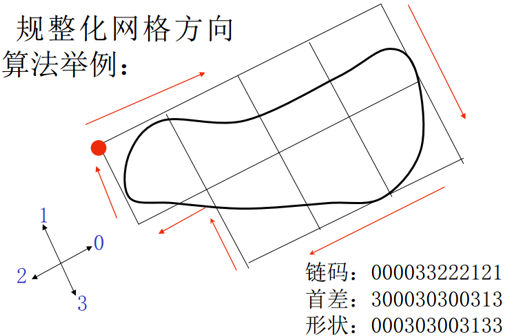
规整化网格方向算法的思想:
大多数情况下,将链码网格与基本矩阵对齐,即可得到一个唯一的形状数。
规整化网格方向的一种算法如下:
(1)首先确定形状数的序号 n;
(2)在序号为 n 的矩形形状数中,找出一个与给定形状的基本矩形的离心率最接近的形状数;
(3)然后再用这个矩形与基本矩形对齐,构造网格;
(4)用获得链码的方法得到链码;
(5)再得到循环首差;
(6)首差中的最小循环数即为形状数。
9.3.3 傅里叶描述子
傅里叶描述子:将一个二维问题简化成一个一维问题
1、基本思想
(1)对于 XY 平面上的每个边界点,将其坐标用复数表示为:
s(k) = x(k) + jy(k),k=0,1,...,N-1
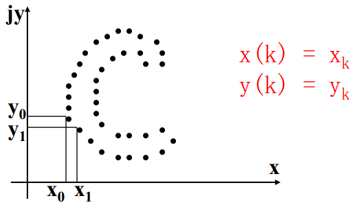
(2)进行离散傅里叶变换
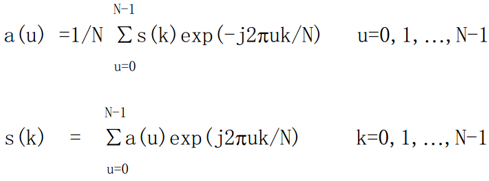
系数 a(u) 被称为边界的傅里叶描述子
(3)选取整数 P≤N-1,进行逆傅里叶变换(重构)

这时,对应于边界点数没有变化,但在重构每一个点所需要的计算项大大减少了。如果边界点数很大,P 一般选为 2 的指数次方的整数。
2、P 的选取与描述符的关系
在上述方法中,相当于对于 u>P-1 的部分舍去不予计算。由于傅里叶变换中高频部分对应于图像的细节描述,因此 P 取得越小,细节部分丢失得越多。
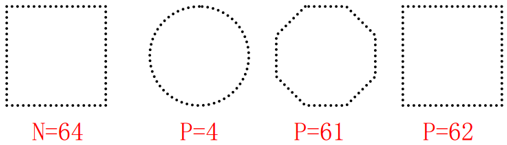
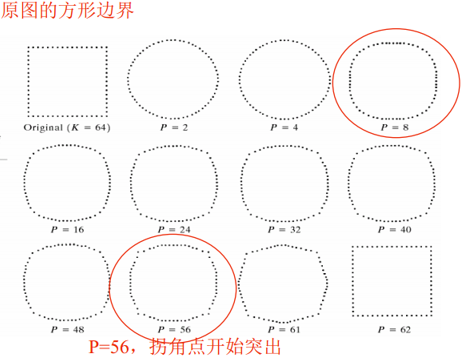
结论:低阶系数能够反映大体形状,高阶系数可以精确定义形状特征,少数傅里叶描述子携带了形状信息,能够反映边界的大略本质。
3、使用价值
(1)较少的傅里叶描述子(如 4 个),就可以获取边界本质的整体轮廓;
(2)这些带有边界信息的描述子,可以用来区分明显不同的边界。
4、优点
(1)使用复数作为描述符,对于旋转、平移、缩放等操作和起始点的选取不十分敏感。
(2)几何变换的描述子可通过对函数作简单变换来获得

9.4 关系描述子
9.4.1 基本思想
通过挖掘各个成分之间的结构关系来描述边界。
图像中各个部分间的结构关系是二维的,而串是一维的,期望找到一种方法把二维关系转化为一维的串。
主导思想是考虑物体各个部分的连接线段。
9.4.2 阶梯关系编码
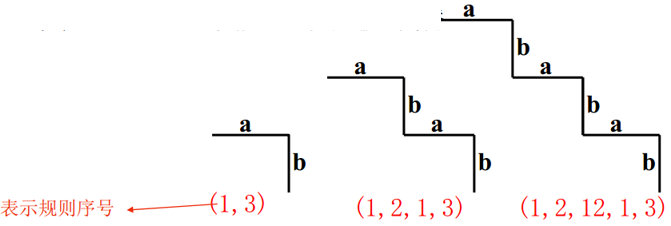
对于如下阶梯形边界,定义两个基本元素 a,b。
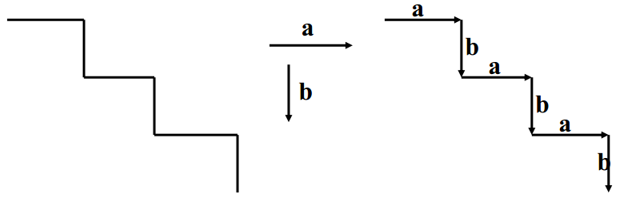
定义如下产生规则:
(1)S → aA 表明起始符 S 可以被图元 a 和变元 A 代替
(2)A → bS 表明变元 A 可以被 b 和 S 代替
(3)A → b 变元 A 可以只被 b 代替
其中 S、A 是变量。
9.4.3 骨架关系编码
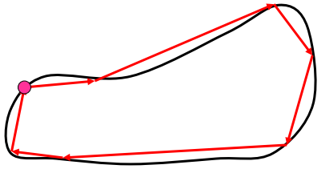
用有向线段来描述一个图像的各个部分(例如同构区域),这个线段是通过头尾连接等方法得到的。线段之间的不同运算代表了区域的不同组合。
当图像的连通性可以通过首尾相接或其它连续的方式描述的时候,最适于使用这种串来描述。

9.4.4 方向关系编码
跟踪对象的边界,将跟踪得到的线段按照方向或长度来编码。
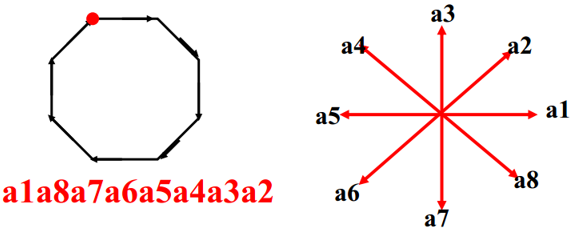
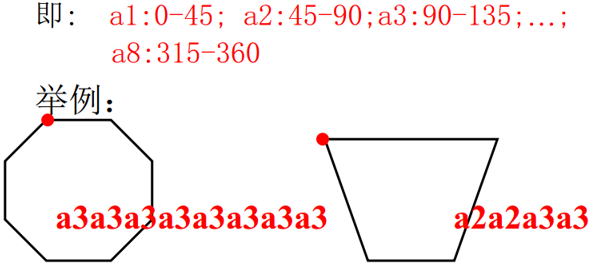
9.4.5 内角关系编码
根据内角角度范围不同,编码为 8 个符号。
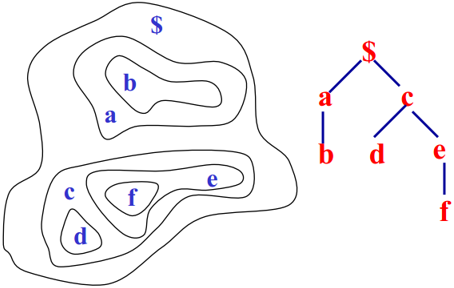
9.4.6 树结构关系
树结构中每个节点的意义和结点之间的关系最为重要。