《图像处理》第7章 形态学图像处理
(仅个人学习摘抄)
膨胀、腐蚀、开操作、闭操作
形态学图像处理的应用可以简化图像数据,保持他们基本的形状特性,并除去不相干的结构。
7.1 基础知识
7.1.1 概述
形态学一般指生物学中研究动物和植物结构的一个分支。用数学形态学(图像代数)表示以形态为基础对图像进行分析的数学工具。
基本思想是用具有一定形态的结构元素去度量和提取图像中的对应形状以达到对图像分析和识别的目的。
形态学图像处理的数学基础和所用语言是集合论。
形态学图像处理基本运算:膨胀、腐蚀、开操作、闭操作。
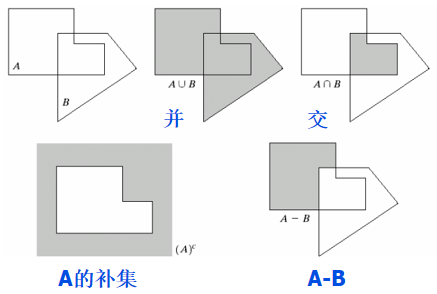
7.1.2 集合理论基础知识
集合的并、交、补、差。


7.2 膨胀和腐蚀
7.2.1 膨胀
膨胀:使图像扩大
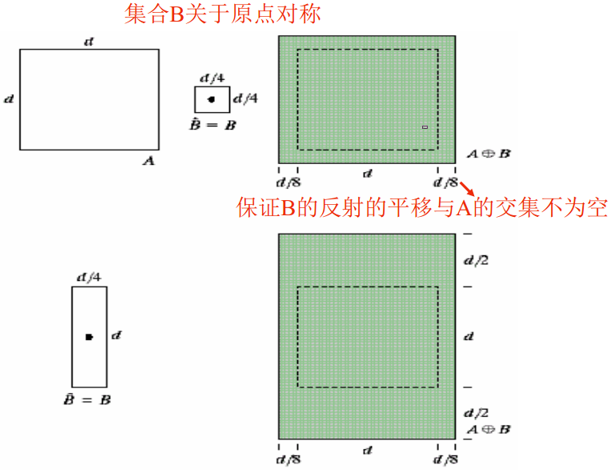
A 和 B 是两个集合,A 和 B 膨胀定义为:

上式表示:B 的反射进行平移与 A 的交集不为空;B 的反射:相对于自身原点的映象;B 的平移:对 B 的反射进行位移。
膨胀的另一个定义:
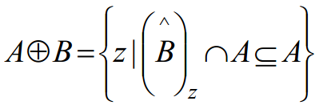
上式表示:B 的反射进行平移与 A 的交集是 A 的子集。
下图表示 A 被 B 膨胀之后的结果:
7.2.2 腐蚀
腐蚀:使图像缩小
A 和 B 是两个集合,A 被 B 腐蚀定义为:
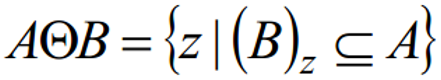
下图表示 A 被 B 腐蚀的结果:
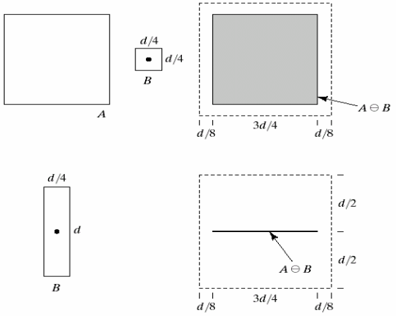
使用腐蚀消除图像的细节部分,产生滤波器的作用。

7.3 开操作和闭操作
7.3.1 开操作
开操作:使图像的轮廓变得光滑,断开狭窄的间断和消除细的突出物。
使用结构元素 B 对集合 A 进行开操作,含义:先用 B 对 A 腐蚀,然后用 B 对结果膨胀。
![]()
A°B 的边界通过 B 中的点完成。B 在 A 的边界内转动时,B 中的点所能到达的 A 的边界的最远点。
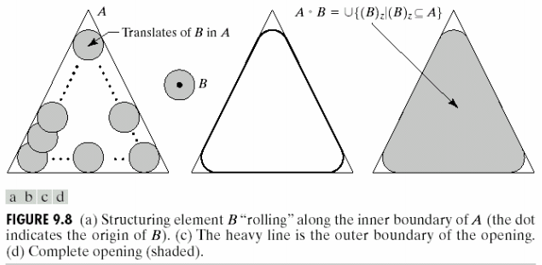
7.3.2 闭操作
闭操作:同样使图像的轮廓变得光滑,但与开操作相反,它能消除狭窄的间断和长细的鸿沟,消除小的孔洞,并填补轮廓线中的裂痕。
使用结构元素 B 对集合 A 进行闭操作,定义为:
![]()
A•B 的边界通过 B 中的点完成。B 在 A 的边界外部转动。

7.3.3 性质
1、开操作的 3 条性质

2、闭操作的 3 条性质

7.4 击中或击不中变换
击中或不击中——形状检测的基本工具
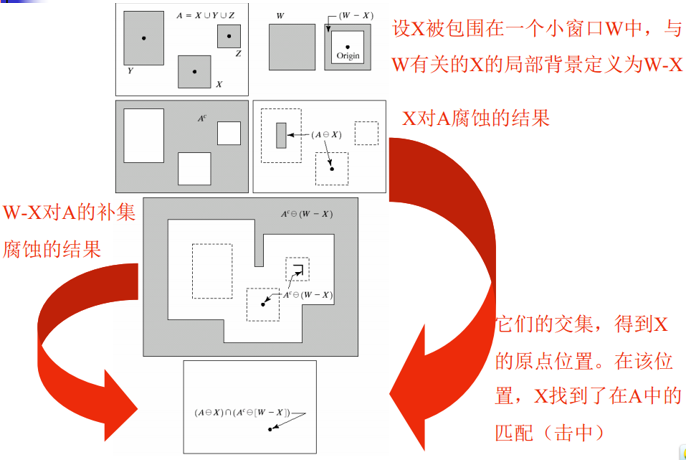
三个相关公式:

7.5 应用
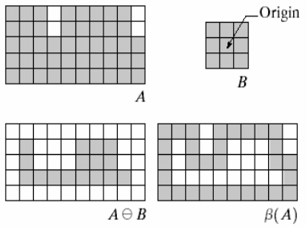
7.5.1 边界提取
边界提取定义:
![]()
上式表示:先用 B 对 A 腐蚀,然后用 A 减去腐蚀的结果,B 是结构元素。
7.5.2 区域填充
区域填充定义为
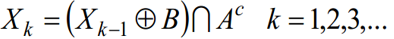
X0=p,如果 Xk=Xk-1,则算法在迭代的第 k 步结束。Xk 和 A 的并集包含被填充的集合和它的边界。
条件膨胀:如果对上述公式的左部不加限制,则上述公式的膨胀将填充整个区域。利用 Ac 的交集将结果限制在感兴趣区域内,实现条件膨胀。
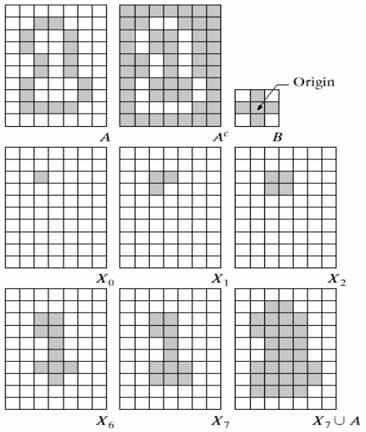
A 中内部区域先被结构元素 B 膨胀得到,根据 A 的补集限制条件,得到最终膨胀结果。
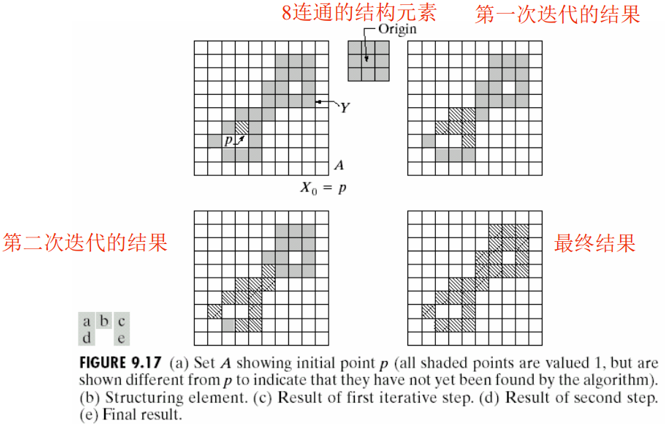
7.5.3 连通分量的提取
连通分量的提取:令 Y 表示一个包含于集合 A 中的连通分量,并假设 Y 中的一个点 p 是已知的。用下列迭代式生成 Y 的所有元素:
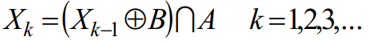
X0=p,如果 Xk=Xk-1,算法收敛,令 Y=Xk。
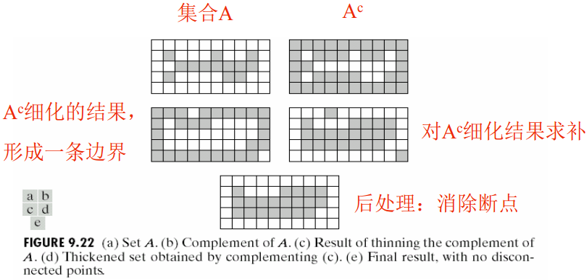
7.5.4 细化
细化过程根据击中或不击中变换定义:

定义结构元素序列为:
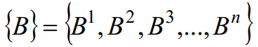
Bi 是 Bi-1 旋转后的形式,如在 B4 中旋转90°
用结构元素序列定义细化为:
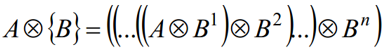
即连续使用 B1,B2,...,Bn 对 A 细化。
7.5.5 粗化
粗化和细化在形态学上是对偶过程,定义为:

用结构元素序列定义粗化为:
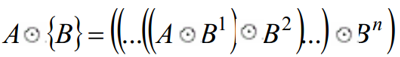
粗化可以通过细化算法求补集实现:
先对所讨论集合的背景进行细化,然后对结果求补集。即:为了对集合 A 进行粗化,先令 C=Ac,然后对 C 进行细化,最后形成Cc