《图像处理》第8章 图像分割
(仅个人学习摘抄)
图像分割是图像识别和图像理解的基本前提步骤,图像分割质量的好坏直接影响后续图像处理的效果。
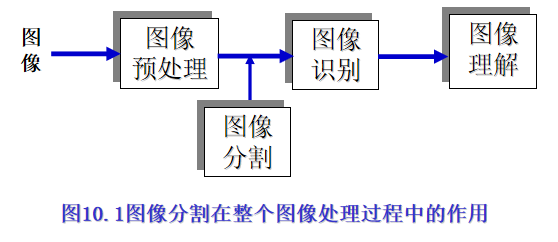
图像分割是指将一幅图像分解为若干互不交叠的、有意义的、具有相同性质的区域。
特征:
(1)分割出来的各区域对某种性质例如灰度,纹理而言具有相似性,区域内部是连通的且没有过多小孔;
(2)区域边界是明确的;
(3)相邻区域对分割所依据的性质有明显的差异。
不同的分割算法总是在不同的约束之间寻找一种合理的平衡。
图像分割算法一般是基于亮度值的两个基本特性之一:不连续性和相似性。
(1)第 1 类性质的应用途径是基于亮度的不连续变化分割图像,比如图像的边缘。
(2)第 2 类的主要应用途径是依据事先制定的规则将图像分割为相似的区域。如:门限(阈值)处理、区域生长、区域分离和聚合。
8.1 间隔检测
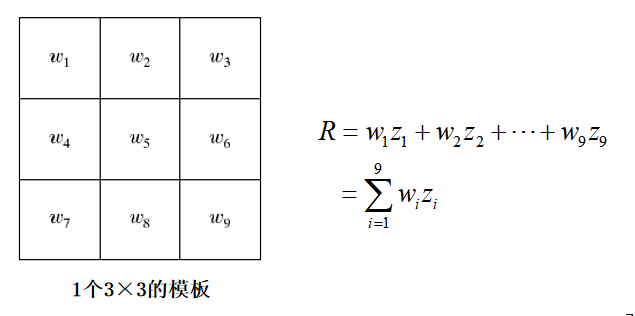
间隔检测的通用方法:
使用一个模板对整幅图像进行检测。
8.1.1 点检测
孤立点的检测
使用如图所示模板,若 |R|≥T,则在模板中心的位置已经检测到一个孤立点。T 为非负门限。
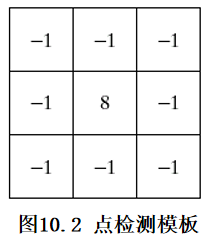
如果一个孤立点与它周围的点很不同,则很容易被这类模板检测到。
8.1.2 线检测
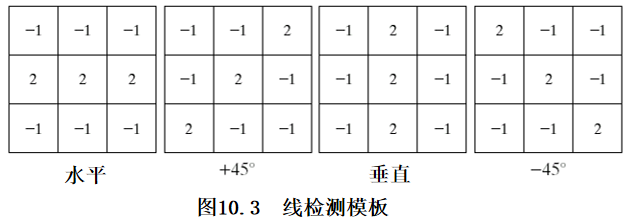
第 1 个模板对水平方向(一个像素宽度)的线条有很强的响应。
第 2 个模板对 +45° 方向有最佳响应。
令 R1,R2,R3,R4分别表示图 10.3 中模板的响应,如果|Ri|>|Rj|,则此点被认为与模板 i 方向上的线更相关。
若要检测特定方向上的线,应使用与这一方向有关的模板,并设置该模板的输出门限。
8.1.3 边缘检测
在边缘处,灰度和结构等信息产生突变,边缘是一个区域的结束,也是另一个区域的开始,利用该特征可以分割图像。
由于图像数据是二维的,而实际物体是三维的,从三维到二维的投影必然会造成信息的丢失,再加上成像过程中光照的不均和噪声等因素的影响,使得有边缘的地方不一定能被检测出来,而检测出来的边缘也不一定代表实际边缘。
图像的边缘有方向和幅度两个属性,沿边缘方向像素变化平缓,垂直于边缘方向像素变化剧烈。边缘上的这种变化可以用微分算子检测出来,通常用一阶或二阶导数来检测边缘。
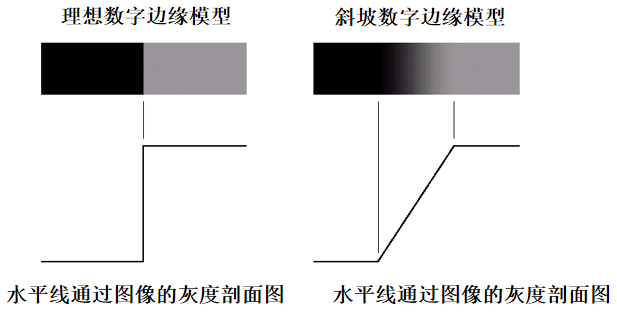
斜坡部分与边缘的模糊程度成正比。
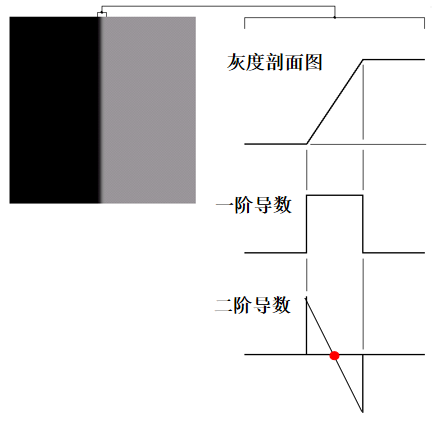
一阶导数可以用于检测图像中的一个点是否在斜坡上。
二阶导数的符号可以用于判断一个边缘像素是在边缘亮的一边还是暗的一边。
(1)对图像中的每条边缘二阶导数生成两个值
(2)一条连接二阶导数正极值和负极值的虚构直线将在边缘中点附近穿过零点,据此可以用于确定粗边线的中心。(如上图)
二阶导数正数表示暗,负数表示亮。
基于一阶导数的边缘检测算子包括 Roberts 算子、Sobel 算子、Prewitt 算子等。通过 2X2 或者 3X3 的模板作为核与图像中的每个像素点做卷积和运算,然后选取合适的阈值以提取边缘。
拉普拉斯边缘检测算子是基于二阶导数的边缘检测算子,对噪声敏感,一种改进方式是先对图像进行平滑处理,然后再应用二阶导数的边缘检测算子。
图像边缘对应一阶导数的极大值和二阶导数的过零点。
梯度算子是一阶导数算子

近似计算:

数字图像处理中用差分代替微分
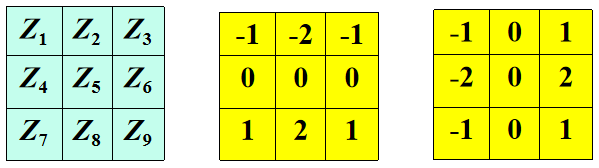
1、Roberts 算子

Gx = Z9 - Z5
Gy = Z8 - Z6
2、Prewitt 算子

Gx = (Z7 + Z8 + Z9) - (Z1 + Z2 + Z3)
Gy = (Z3 + Z6 + Z9) - (Z1 + Z4 + Z7)
3、Sobel 算子
Gx = (Z7 + 2Z8 + Z9) - (Z1 + 2Z2 + Z3)
Gy = (Z3 + 2Z6 + Z9) - (Z1 + 2Z4 + Z7)
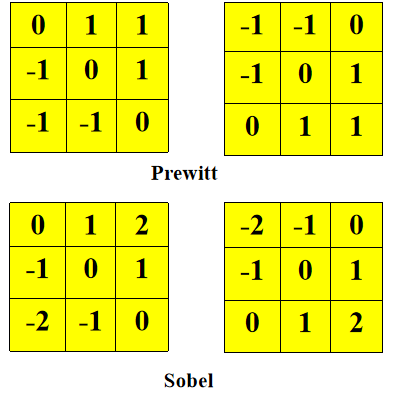
用于检测对角边缘的 Prewitt 算子和 Sobel 算子:
4、拉普拉斯算子
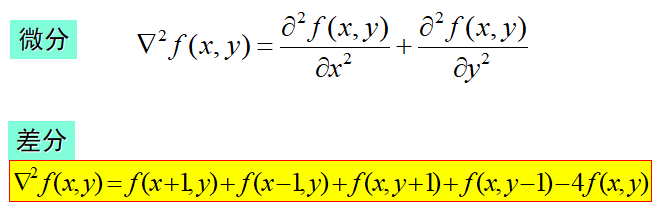
两种常用的拉普拉斯算子模板:
拉普拉斯算子一般不以其原始形式用于边缘检测,这是因为:
(1)作为一个二阶导数,拉普拉斯算子对噪声具有无法接受的敏感性;
(2)拉普拉斯算子的幅值产生双边缘,这是复杂的分割不希望有的结果;
(3)拉普拉斯算子不能检测边缘的方向。
拉普拉斯算子在分割中起的作用包括:
(1)利用它的零交叉的性质进行边缘定位;
(2)确定一个像素是在边缘暗的一边还是亮的一边。
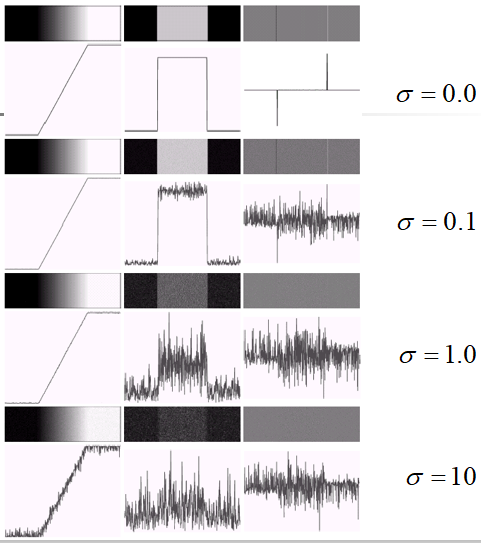
噪声对边缘检测的影响:
5、高斯—拉普拉斯算子
考虑函数: 模糊图像
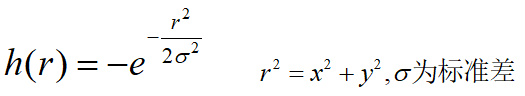
h 的拉普拉斯算子(h 关于 r 的二阶导数):
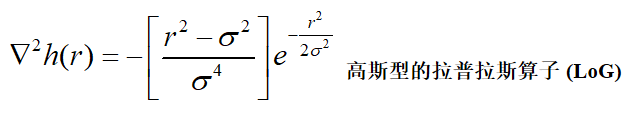
用该函数对图像进行平滑滤波,然后再应用拉普拉斯算子。
算子比较:
Roberts算子:Roberts算子利用局部差分算子寻找边缘,边缘定位精度较高,但容易丢失一部分边缘,同时由于图像没经过平滑处理,因此不具备抑制噪声的能力。该算子对具有陡峭边缘且含噪声少的图像效果较好。
Sobel算子和Prewitt算子:都是对图像先做加权平滑处理,然后再做微分运算,所不同的是平滑部分的权值有些差异,因此对噪声具有一定的抑制能力,但不能完全排除检测结果中出现的虚假边缘。虽然这两个算子边缘定位效果不错,但检测出的边缘容易出现多像素宽度。
Laplacian算子:是不依赖于边缘方向的二阶微分算子算子,对图像中的阶跃型边缘点定位准确,该算子对噪声非常敏感,它使噪声成分得到加强,这两个特性使得该算子容易丢失一部分边缘的方向信息,造成一些不连续的检测边缘,同时抗噪声能力比较差。
8.2 门限处理(阈值分割)
由于图像门限处理的直观性和易于实现的性质,使它在图像分割应用中处于中心地位。
8.2.1 基本原理
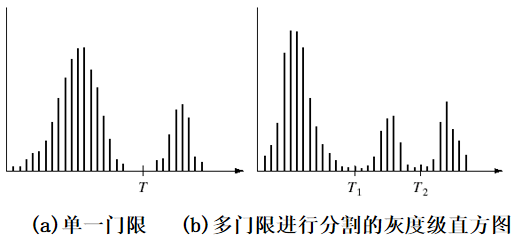
图(a)为一幅图像的灰度级直方图,其由亮的对象和暗的背景组成。对象和背景的灰度级形成两个不同的模式。选择一个门限值 T,可以将这些模式分开。(b)包含三个模式。

原始图像 —— f(x,y)
灰度阈值 —— T
阈值运算得二值图像 —— g(x,y)
阈值选择直接影响分割效果,通常可以通过对灰度直方图的分析来确定它的值。
图像分割之后,即经过阈值处理之后,图像变成二值化图像。
8.2.2 阈值选择
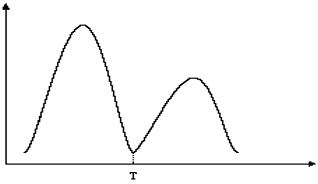
利用灰度直方图求双峰或多峰,选择两峰之间的谷底作为阈值。
1、人工阈值
人工选择法是通过人眼的观察,应用人对图像的认识,在分析图像直方图的基础上,人工选择出合适的阈值。也可以在人工选出阈值后,根据分割效果,不断的交互操作,从而选择出最佳的阈值。
2、自动阈值(迭代法)
在无人介入的情况下自动选取阈值时大部分应用的基本要求,自动阈值法通常使用灰度直方图来分析图像中灰度值的分布,结合特定的应用领域知识来选取合适的阈值。
基本思想:开始时选择一个阈值作为初始估计值,然后按某种策略不断地改进这一估计值,直到满足给定的准则为止。在迭代过程中,关键之处在于选择什么样的阈值改进策略,好的阈值的改进策略应该具备两个特征,一是能够快速收敛,二是在每一个迭代过程中,新产生阈值优于上一次的阈值。
迭代式阈值选择的基本步骤如下:
(1)选择图像灰度的中值作为初始阈值 Ti = T0
(2)利用阈值 Ti 把图像分割成两部分区域,R1 和 R2,并计算其灰度均值
(3)计算新的阈值 Ti+1


(4)重复步骤 2、3,直到 Ti+1 和 Ti 的值差别小于某个给定值
8.3 区域分割
基本思想
阈值分割法由于没有或很少考虑空间关系,使多阈值选择受到限制。
基于区域的分割方法可以弥补这点不足,它利用的是图像的空间性质,该方法认为分割出来的属于同一区域的像素应具有相似的性质,其概念是相当直观的。
传统的区域分割算法有区域生长法和区域分裂合并法。该类方法在没有先验知识可以利用时,对含有复杂场景或自然景物等先验知识不足的图像进行分割,也可以取得较好的性能。但是,空间和时间开销都比较大。
基本公式
形式化地定义如下:令 I 表示图像,H 表示具有相同性质的谓词,图像分割把 I 分解成 n 个区域 Ri,i=1,2,...,n,满足:
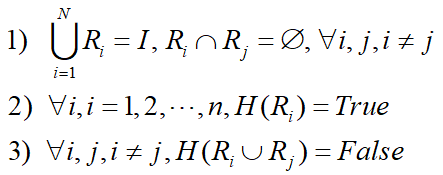
条件(1)表明分割区域要覆盖整个图像且各区域互不重叠;
条件(2)表明每个区域具有相同的性质;
条件(3)表明相邻的两个区域性质相异不能合并为一个区域。
8.3.1 区域生长
区域生长是一种根据事前定义的准则将像素或子区域聚合成更大区域地过程。
区域生长主要考虑像素及其空间邻域像素之间的关系
开始时确定一个或多个像素点作为种子,然后按某种相似性准则增长区域,逐步生成具有某种均匀性的空间区域,将相邻的具有相似性质的像素或区域归并从而逐步增长区域,直至没有可以归并的点或其它小区域为止。
区域内像素的相似性度量可以包括平均灰度值、纹理、颜色等信息。
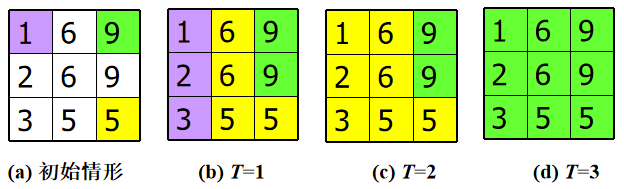
生长准则:所考虑的像素点和种子点地灰度值地绝对值差小于或等于某个阈值 T,将该像素点归入种子点所在的区域。
区域生长步骤:
(1)选择合适的种子点
(2)确定相似性准则(生长准则)
(3)确定生长停止条件
8.3.2 区域分裂
如果区域的某些特性差别比较大,即不满足一致性准则时,则区域应该采用分裂法,分裂过程从从图像的最大区域开始,一般情况下,是从整幅图像开始。
注意:
(1)确定分裂准则(一致性准则)
(2)确定分裂方法,即如何分裂区域,使得分裂后的子区域的特性尽可能都满足一致性准则值
算法:
(1)形成初始区域;
(2)对图像的每一个区域 Ri,计算 P(Ri),如果 P(Ri)=FALSE,则沿着某一合适的边界分裂区域;
(3)重复步骤(2),当没有区域需分裂时,算法结束。
8.3.3 区域合并
单纯的区域分裂只能把图像分成许多满足一致性谓词的区域,相邻的具有相同性质的区域并没有合成一体。
(1)合并运算就是把相邻的具有相似性质的区域合称为一个区域
(2)合并算法中最重要的运算是确定两个区域的相似性
(3)评判区域相似性方法有许多,评判相似性的方法可以基于区域的灰度值,也可以基于边界的强弱性等因素。一种简单的方法是比较它们的灰度均值。
算法:
(1)使用某种方法进行图像的初始区域分割。
(2)对于图像中相邻的区域,计算是否满足一致性谓词,若满足则合并为一个区域。
(3)重复步骤(2),知道没有区域可以合并,算法结束。
8.3.4 区域分裂合并
区域分裂合并法无需预先指定种子点,它按某种一致性准则分裂或者合并区域。可以先进行分裂运算,然后再进行合并运算;也可以分裂和合并运算同时进行,经过连续的分裂和合并,最后得到图像的精确分割效果。
分裂合并法对分割复杂的场景图像比较有效。
具体实现时,分裂合并算法可以基于四叉树数据表示方式进行。
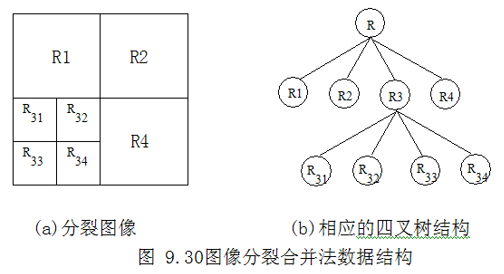

算法:
(1)设整幅图像为初始区域;
(2)对每个区域 R,如果 P(R)=FALSE,则把该区域分裂成四个子区域;
(3)重复上一步,直到没有区域可以分裂;
(4)对图像中任意两个相邻的 R1 和 R2,如果 P(R1UR2)=FALSE,则把这两个区域合并成一个区域;
(5)重复上一步,直到没有相邻区域可以合并,算法结束。




