《人工神经网络》第9章 遗传算法原理
(仅是自己学习的摘抄)
遗传算法 GA(Genetic Algorithm)是一种根据生物学中所谓自然选择和遗传机理的随机搜索优化算法。遗传算法的主要特点是群体搜索策略和群体中个体之间的信息交换,搜索不依赖于传统方法中常用到的梯度信息。适合于处理传统搜索方法难于解决的复杂和非线性问题。遗传算法给出了一个用来解决高度复杂问题的新思路和新方法。遗传算法已经应用在许多实际问题,如函数优化、自动控制、图像识别、机器学习、人工神经网络、优化调度等。
9.1 概述
遗传算法是基于自然选择和基因遗传学原理的随机搜索算法。
遗传算法的核心问题是寻找求解优化问题的效率与稳定性之间的有机协调性,即鲁棒性(Robustness)。人工系统一般很难达到如生物系统那样的鲁棒性。遗传算法在吸收了自然生物系统“适者生存”的进化原理之后,从而使它能够提供一个在复杂空间中进行鲁棒搜索的方法。由于遗传算法具有计算简单和功能强大的特点,它对于参数搜索空间基本上不要求苛刻的条件(如连续、导数存在以及单峰等),故广泛应用。
遗传算法是采用随即技术的一种随机搜索方法,但不同于一般的随机搜索方法。遗传算法通过将待寻优参数空间进行编码,并用随机选择作为工具来引导搜索过程向着更高效的方向发展。
遗传算法的主要特点:
(1) 遗传算法是对要寻优参数的编码进行操作,而不是对参数本身。
(2) 遗传算法是从“群体”出发(多个初始点)开始的并行操作,而不是从一个点开始。因而可以有效地防止搜索过程收敛于局部最优解,而且有较大的可能求得全局最优解;所以遗传算法具有并行计算的特点,可通过大规模并行计算来提高计算速度。
(3) 遗传算法采用目标函数(适配值)来确定基因的遗传概率,而不需要其他的推导和附属信息,从而对问题的依赖性较小。所以遗传算法对于待寻优的函数基本无限制,它既不要求函数连续,更不要求可微,既可是数学解析式所表达的显函数,又可以是其它方式的隐函数甚至是神经网络等隐函数,因而应用范围较广。
(4) 遗传算法的操作均使用随机概率的方式,而不是确定性的规则。
(5) 遗传算法在解空间内不是盲目地穷举或完全随机测试,而是一种启发式搜索,其搜索效率往往优于其它方法。
(6) 遗传算法更适合大规模复杂问题的优化。
9.2 遗传算法的工作原理
9.2.1 遗传算法的编码、再生、交叉与变异
设优化问题的目标函数为:
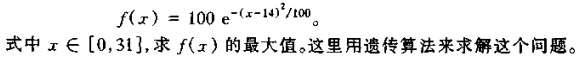
(1)初始化编码
遗传算法的第一步是将 x 编码为有限长度的串。编码方法有很多种,这里针对自变量的定义域,考虑采用二进制数对 x 编码,x 恰好用 5 位二进制数来表示。
许多其他的优化方法是从定义域空间的某个初始点出发并根据某些算法来求解,相当于按照一定的路线,进行点到点的顺序搜索,如单纯形法、爬山法等,这对于多峰值问题的求解很容易陷入局部极值。遗传算法是从一个种群(由若干个编码串组成,每个串对应一个自变量值)开始,不断地产生和测试新一代的种群。这种方法从开始就具有了较大搜索空间范围,从而可望较快地完成优化问题的求解。
初始种群的生成用随机方法生成。
(2)再生
再生过程是将个体编码串按照它们的适配值(目标函数值)进行再生。显然,目标函数是待优化问题的指标,等价于神经网络动力学模型中的能量函数,物理意义上如利润、功率、时间等的物理量,其值越大或越小,越满足优化的需要。这里统一按取最大值考虑,即按照配值进行串再生的本质是:适配值越大的串,将有更多的机会对下一代提供一个或多个子孙。这个操作步骤主要是模仿自然选择现象,将适者生存理论运用于串的再生。此时,适配值相当于自然界中的一个生物为了生存所具备的各项能力的大小,它决定了该串是被再生还是被淘汰的概率。
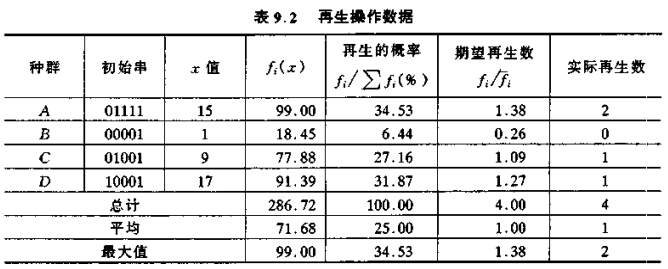
再生操作通过随机方法来实现。考虑先产生 0~1 之间均匀分布的随机数 ζ,某串的再生概率就规定了该随机数的产生区间。如产生的随机数在 0.11≤ ζ < 0.42 之间时,该串被再生的概率即为 31%。在一轮(群体的个体数,本例为 4 次)的再生后,没有被再生的个体串就被淘汰。下表给出了每个个体串被再生的概率。
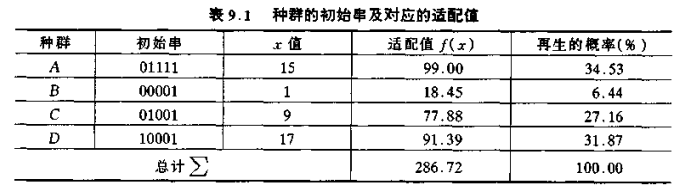
再生操作的方法可用轮盘赌的转盘方式来形象地说明。
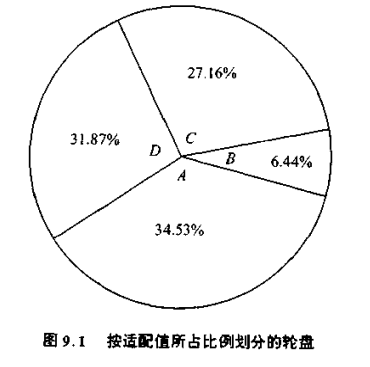
再生过程就是 4 次旋转这个经过划分的轮盘,从而产生 4 个下一代的种群。对应较大的适配值的串将在下一代中有较多的子孙。当某一串被选中时,此串将被完整地再生,然后将再生串添入匹配池(Matching Pool,匹配池是对串进行匹配操作的地方)。因此旋转 4 次轮盘即产生出 4 个串。这 4 个串是上一代种群的选择式再生,有的串可能被再生一次或多次,有的可能被淘汰。本例,经再生后的新种群为:
01001,01111,10001,01111
这里的串 A 被再生了两次,串 B 被淘汰,串 C、串 D 各被再生了一次。
(3)交叉
① 匹配
将新再生产生的匹配池中的成员随机两两匹配。随机地将匹配池中的个体配对,本例中。匹配的结果是串 A 和串 B 配对,C 和 D 配对。串 A 和 B,C 和 D 分别成为了父母串。
② 交叉繁衍
设串的长度(二进制数的位数)为 l。则串的 l 个数字位之间的空隙标记为 k,k = 1,2,...,l-1。随机地从 [1,l-1] 中选取整数 k,则将两个父母串从位置 k 到串末尾的子串互相相交换,从而形成两个新的子孙串。

本例交叉操作结果如下: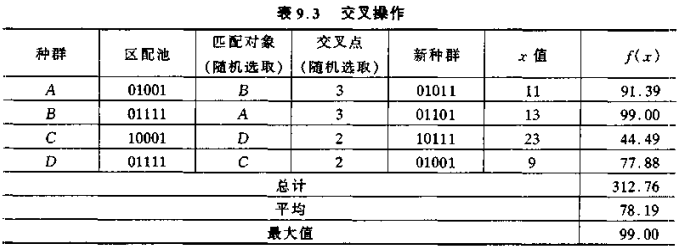
(4)变异
变异对应于基因变化。这个操作相对于再生和交叉操作而言,是一项必要但发生概率较小的操作。变异的目的是为了防止丢失一些有用的遗传因子,特别是当种群中的个体,经遗传运算可能使某些串位的值失去多样性,从而可能失去检验有用遗传因子的机会时,变异操作可以起到恢复串位多样性的作用。变异操作是以很小的概率随机地改变某一个串位的值。变异的概率通常是很小的,一般按千分之几给出。对于本例,变异概率可取为 0.001,则对于种群的总串位(4 x 5 = 20),期望的变异串位数为 20 x 0.001 = 0.02(位),所以本例中不作串位值的改变。
从表9.2和表9.3 可以看出,在经过一次再生、交叉和变异操作后,种群的平均适配值从 71.68 增至 78.19,而最大的适配值保持不变,均为 99.00。每经过这样的一次遗传算法过程,优化问题的解便朝着最优解方向前进了一步。随着再生、交叉和变异操作的不断进行,它将最终获得全局最优解。
9.2.2 遗传算法的工作机理
9.2.2.1 串模式
示例中可知,某些子串模式(Schemata)在遗传算法的运行中起着关键性的作用。这些子串模式是那些再生概率大的个体串,即接近 x =14 的编码个体串,它们的编码串的首位为“0”。对于本例的函数及 x 的编码方式很容易验证这一点。
引入通配符 *,* 既可代表“1”,也可代表“0”,这就给出了串模式的概念。如首位为“1”的子串可以表示成这样的模式:1 * * * *;首位为“0”的子串可以表示为:0 * * * *;第三位为“0”的串模式为:* * 0 * *,以此类推。
上面给的示例中模式(0 * * * *)在遗传算法的一代一代运行过程中不仅保留了下来,而且数量不断增加。由于这种适配值高的模式不断增加,就使得求解问题的算法性能不断改进。
一般地,对于二进制串,在 {0,1} 字符串中间加入通配符“ * ”,即可生成所有可能模式。因此用 {0,1,* } 可以构造出任意一种模式。某一个模式与一个特定的串相匹配是指:该模式中的“1”与串中的“1”相匹配,模式中的“0”与串中的“0”相匹配,模式中的“ * ”匹配串中的“0”或“1”。

用模式阶数和定义长度来描述模式的属性。
[ 定义 9.1 ] 模式阶数 O:一个模式 H 的阶数由 O(H) 表示,它等于模式中确定位置(对于二进制,即 0 或 1 所在的位置)的个数。如模式 H= * 0 1 * 1 * 0,其阶数为 4,记为 O(H) = 4,若 H = * * 1 * * * *,则 O(H) = 1。
[ 定义 9.2 ] 模式定义长度 δ:模式 H 的定义长度为模式中第一个和最后一个确定位置之间的距离。如模式 H = 1 * 1 0 * *,δ(H) 4 -1 = 3。若模式 H = * * * * * * 1,则 δ(H) = 0。
9.2.2.2 再生、交叉、变异对模式的影响
(1)再生对模式的作用
设对于时间 t,种群 S(t) 包含 m 个特定模式 H,记为:
m = m (H,t)

经过再生操作后,特定模式的数量将按照该模式的平均适配值与整个种群平均适配值的比值成比例地改变。换而言之,适配值高于种群平均适配值的模式在下一代中的数量将增加,而低于平均适配值的模式在下一代中的数量将减少。另外,种群 S 的所有模式 H 的处理是并行进行的,即所有模式经再生操作后,均同时按照其平均适配值占总体平均适配值的比例予以减少。所以再生操作对模式的影响是,使得高于平均适配值的模式数量增加,低于平均值的数量减少。

再生过程成功地以并行方式控制着模式数量以指数形式增减,但由于再生只是将某些高适配值个体全盘再生,或是丢弃某些低适配值个体,而绝不会产生新的模式结构,因而性能的改进是有限的。
(2)交叉对模式的作用
交叉过程是串之间有组织而又是随机的信息交换,它在产生新串的同时,最低限度地破坏再生过程所选择的高适配值模式。
考察一个 l = 7 的串以及串所包含的两个代表模式:


(3)变异对模式的作用
对串中的某个基因以概率 pm 进行随即替换称为变异。这种随即替换可能会破坏某一特定的模式。一个模式 H 要存活等价于它所有的确定位置都要保存下来。因此,由于单个基因值存活的概率为(1-pm),而且由于每个变异的发生都是统计独立的,而一个特定模式 H 的阶数给出了该模式的所有确定的位置,所以一个特定模式仅当它的 O(H) 个确定位置都存活时才存活。从而经变异后,特定模式的存活率应为(-pm)O(H)。

[ 定理 9.1 ] 模式定理对于那些短定义长度、低次数、高于平均适配值的模式将在后代中呈指数级的增长。
根据模式定理,随着遗传算法的再生、交叉、变异等操作一代一代地进行,那些短的、低次数的、高适配值的模式将越来越多,最后得到的串即是这些模式的组合。因而可期望算法性能越来越得到改善,并最终向全局的最优点发展。




