《图像处理》 第2章 相关图像基础
(仅是个人学习摘抄)
2.2 图像成像过程
成像时要考虑三个方面的问题:
1、几何关系:在图像什么地方可以发现目标?
2、辐射特性:图像中的目标有多亮,该亮度与目标和成像系统的光学特征有什么关系?
3、数字化和量化:当用一个数字矩阵表达图像并用数字计算机处理该图像会得到什么结果?
2.2.1 成像变换
投影成像:将3-D客观场景投影到2-D图像平面
成像过程:从 XYZ 到 xyz,从 xyz 到 xy
世界坐标系统 XYZ
摄像机坐标系统 xyz
图像平面 xy
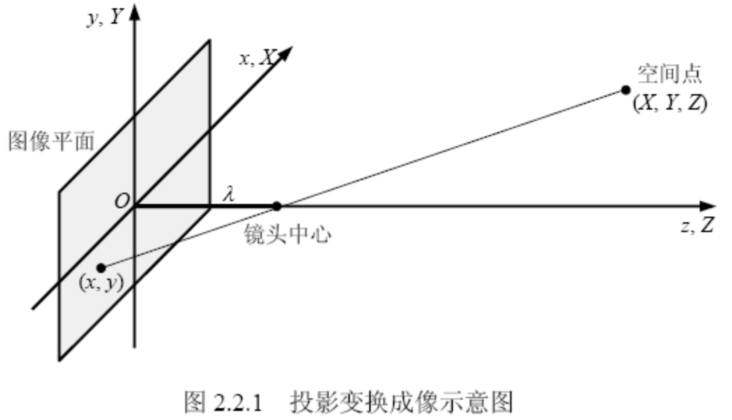
透视变换:(1)3-D投影后的图像平面坐标
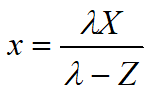
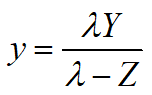
(2)非线性投影等式(分母含变量 Z)
齐次坐标:可以来将上面的非线性(分母含变量 Z)等式可以表示成线性矩阵形式
笛卡尔坐标:![]()
齐次坐标:![]()
k 是任意非零常数
齐次坐标->笛卡尔坐标:用第 4 个坐标量去除前 3 个坐标量
齐次坐标透视变换:3-D 转 2-D

用第 4 项分别除去前 3 个项
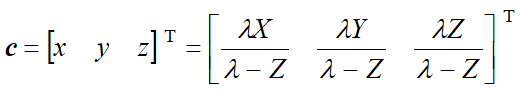
逆投影变换:根据 2-D 图像坐标来确定 3-D 客观景物的坐标
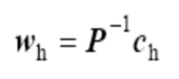
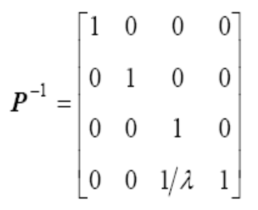
2.2.2 成像亮度
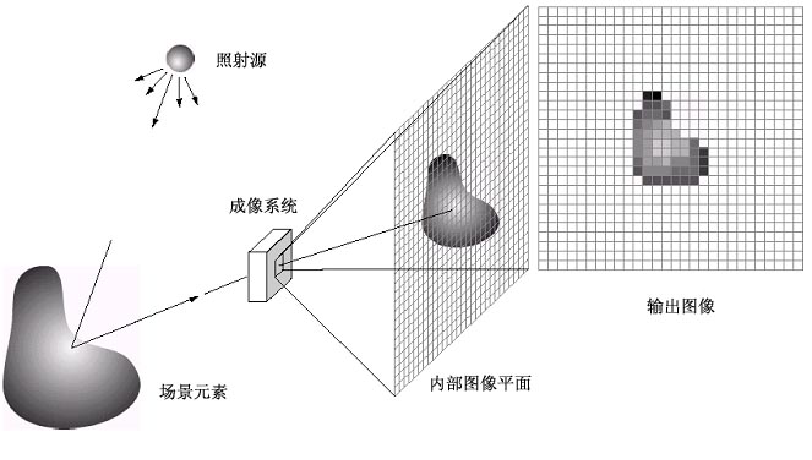
图像中目标的亮度取决于:景物所受的光照度;景物表面对光的反射程度;成像系统的特性。
2.2.3 采样和量化
图像->数字图像
f(x,y)->I(r,c)
空间坐标的离散化叫做空间采样 x,y -> r,c
幅度的离散化叫做幅度量化 f -> I
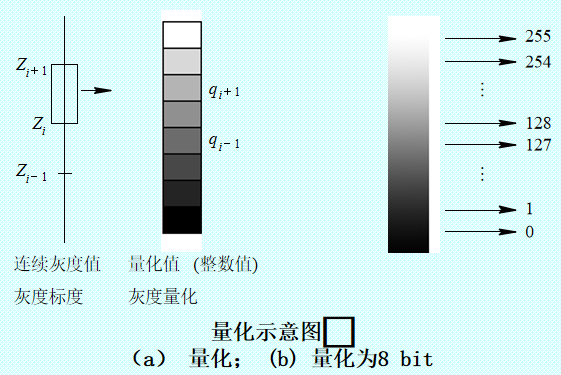
量化使图像有幅度(灰度)分辨率
采样使图像有空间分辨率
数字图像的位数 b = M × N × k = N2k
M:图像(水平)尺寸;N:图像(垂直)尺寸;像素灰度级数 G(k-bit):G = 2k
空间分辨率:图像空间中可分辨的最小细节。一般用单位长度上采样的像素数目或单位长度上的线对数目表示。
灰度分辨率:图像灰度级中可分辨的最小变化。一般用灰度级或比特数表示。
空间分辨率越高,图像质量越好,但占空间大。反之,会出现棋盘模式。
灰度分辨率越高,量化级数越大,图像质量越好。反之,会出现虚假轮廓。
采样量化原则:
当限定数字图像大小时,为了得到质量较好的图像,采用如下原则:
1、对缓变的图像。细量化,粗采样,避免假轮廓。
2、对细节丰富的图像,细采样,粗量化,以避免模糊。
2.3 离散距离及扩散
2.3.1 像素间的联系
图像由像素组成,像素在图像空间上按规律排列,相互之间有一定的联系
1、邻接关系:邻域或连接
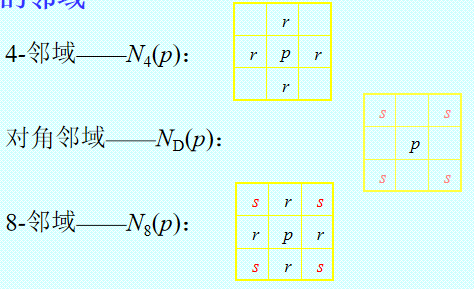
邻接(adjacency)VS 连接(connectivity)
邻接:只考虑像素间的空间关系
判断两个像素是否连接:(1)是否接触(邻接);(2)灰度值是否满足某个特定的相似准则:同在一个灰度值集合(值域V)取值
3种连接:
(1)4-连接:2个像素 p 和 r 在 V 中取值且 r 在 N4(p)中
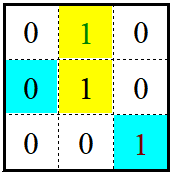
p、r 的灰度值都为 1,黄色区域
(2)8-连接:2个像素 p 和 r 在 V 中取值且 r 在 N8(p)中
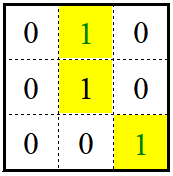
黄色区域,r 是绿色的 1
(3)m-连接(混合连接)
2个像素 p 和 r 在 V 中取值,且满足下列条件之一:
① r 在N4(p)中
② r 在ND(p)中且集合N4(p)∩N4(r)是空集,即集合中没有 V 值的像素
混合连接可以消除8-连接可能产生的歧义性
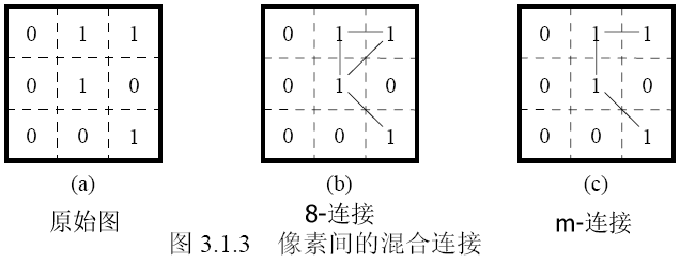
2、连通关系:连通性
连接是连通的一种特例。
通路:由一系列依次连接的像素组成。


8-连通:红色,绿色
m-连通:绿色(印证了m-连接消除了8-连接产生的歧义性)
像素集合的邻接和连通
对2个图像子集 S 和 T 来说,如果 S 中的一个或一些像素与 T 中的一个或一些像素邻接,则可以说 2 个图像子集 S 和 T 是邻接的。
完全在一个图像子集中的像素组成的通路上的像素集合构成该图像子集中的一个连通组元。
如果 S 中只有 1 个连通组元,即 S 中所有像素都互相连通,则称 S 是一个连通集。
3、距离关系:距离度量
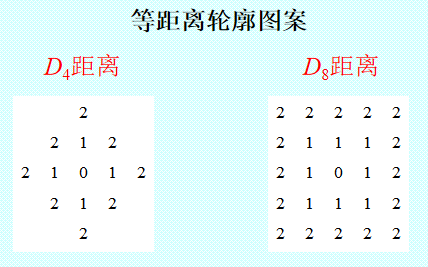
2.3.2 常用离散距离
距离度量函数:

距离量度函数:欧式(Euclidean)距离、城区(city-block)距离、棋盘(chessboard)距离
用距离定义邻域
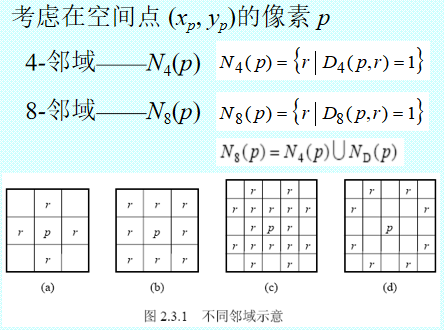
16-邻域——N16(p) 图(c)
马步距离是按国际象棋棋盘上从一格运动到另一格所需步数来计算的 图(d)
离散元盘
中心为像素 p 的半径为 r(r ≥ 0)的圆盘是满足 ΔD(p,r) = {q | dD(p,q)≤r}的点集
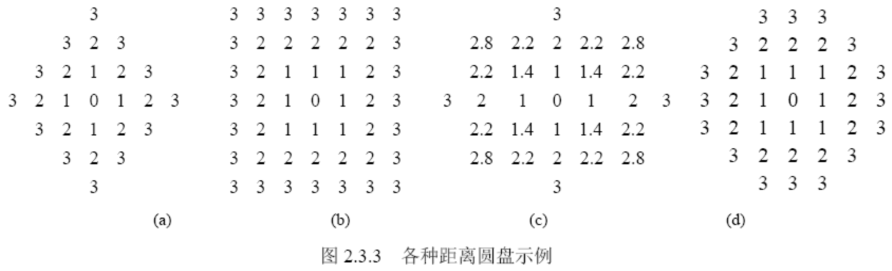
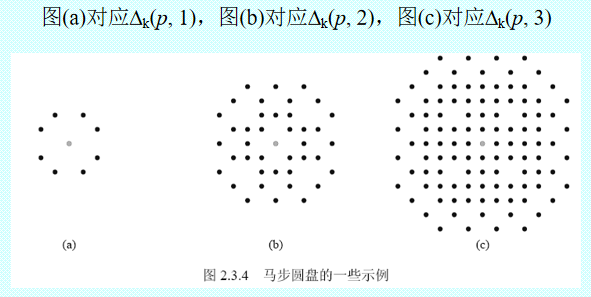

N16空间和其中的连通性
一个像素和它的 16-邻域像素组成 N16空间
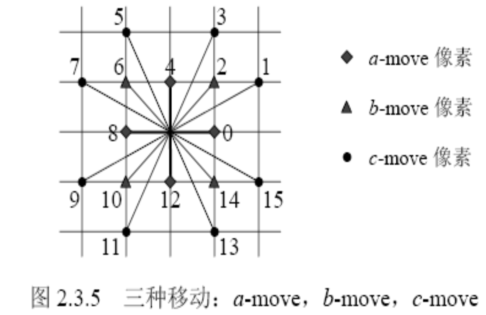
(1) 水平和垂直移动 a-move
(2) 对角线移动 b-move
(3) 马步移动 c-move
斜面距离:
4-邻域:斜面距离就是 d4 距离,其中 a = 1
8-邻域:斜面距离为 da,b 距离,其中 a = 3,b = 4。0 < a ≤ b ≤ 2a
16-邻域:斜面距离为 da,b,c 距离,其中 a = 5,b = 7,c = 11
0 < a ≤ b ≤ 2a ≤ c;c ≤ a + b;3b ≤ 2c
2.4 图像噪声消除
噪声:图像中不希望有的部分,不需要的部分
特点:可以有一定的随机性(电视屏幕上椒盐噪声)、可以比较规律或有规律(山谷中的回声仅有一定的延迟)
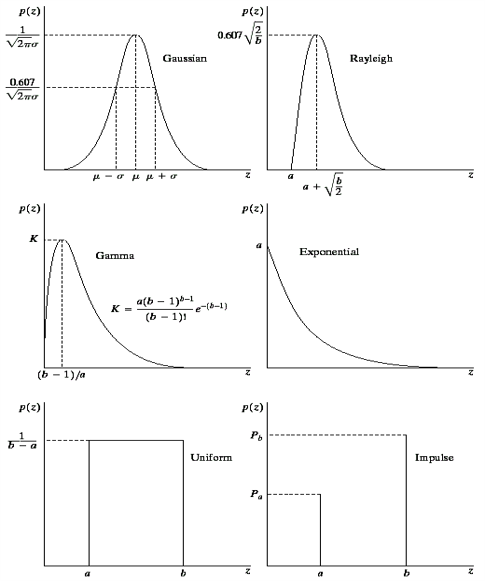
噪声模型:高斯(Gaussian)噪声、瑞利(Rayleigh)噪声、伽马(爱尔兰)噪声、指数(Exponential)噪声、均匀(Uniform)噪声、脉冲(椒盐)噪声
2.4.1 线性滤波消除噪声
1、空域滤波原理
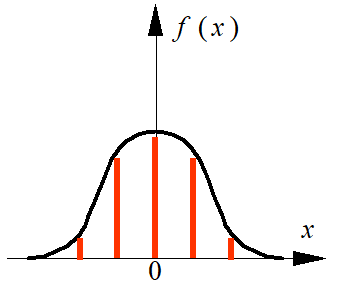
在频域分析,在空域进行;平滑滤波;空域里的剖面图;系数都是正的(中心系数大,周围系数小)
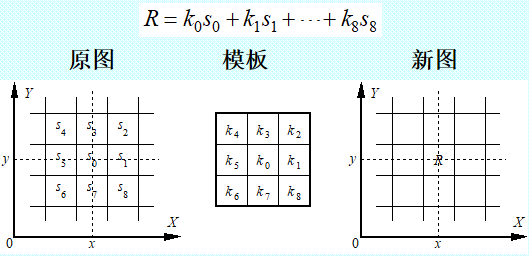
模板卷积(尺寸 n x n,半径 r = (n-1)/2 )
(1)将模板在图中漫游,并将模板中心与图中某个像素位置重合
(2)将模板上的各个系数与模板下各对应像素的灰度值一一相乘
(3)将所有乘积相加(为保持灰度范围,常将结果再除以模板的系数个数)
(4)将上述运算结果(模板的输出响应)赋给图中对应模板中心位置的像素
2、空域平滑滤波
邻域平均:保持灰度值范围(所有系数之和为 1)

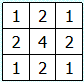
加权平均:为保证各模板系数均为整数以减少计算量,常取模板周围最小的系数为 1;根据系数与模板中心的距离反比地确定其它内部系数的值
2.4.2 非线性滤波消除噪声
1、中值滤波
令N(x, y)为(x, y)的邻域(模板覆盖)
![]()
模板尺寸 n x n 的中值滤波器的输出值应 ≤ 模板中(n2-1)/2个像素的值,又应 ≥ 模板中(n2-1)/2个像素的值。
中值滤波器的主要功能就是让与周围像素灰度值的差比较大的像素改取与周围像素值接近的值。
一般情况下,图像中尺寸小于模板尺寸一半的过亮和过暗区域将会在滤波后被消除掉。
中值滤波的过程:
(1) 将模板在图中漫游,并将模板中心与图中某个像素位置重合
(2) 读取模板下各对应像素的灰度值
(3) 将这些灰度值从小到大排成一列
(4) 找出这些值里排在中间的一个
(5) 将这个中间值赋给对应模板中心位置的像素
特点:即能消除噪声又能保持图像的细节
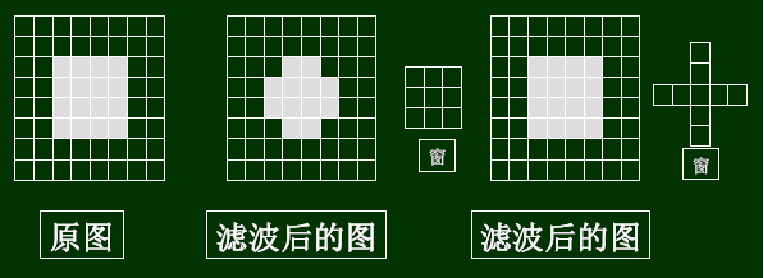
中值滤波的模板:
中值滤波器的消噪声效果与模板的尺寸,参与运算的像素数有关。
图像中小于模板尺寸一半的过亮或过暗区域将会在滤波后被消除掉。
中值滤波的结果与窗口的形状有关
自适应中值滤波器:
相对来说,中值滤波器对脉冲噪声工作得够好(只要脉冲噪声的空间密度不要太大)。自适应中值滤波器能够处理更好空间密度的脉冲噪声,而且能够处理一些非脉冲噪声的平滑效果。理解自适应中值滤波器,关键是要知道滤波器大小随着图像特征而改变。
滤波过程是顺序遍历原始图像中的每个像素,并产生一个滤波像素。
zmin = Sxy中的灰度级最小值
zmax = Sxy中的灰度级最大值
zmed = Sxy中的灰度级中值
zxy = 坐标(x, y)处的灰度级
Smax = Sxy允许的最大尺寸
自适应中值滤波器算法工作在两个层次,定义为 A 层和 B 层
A 层:A1 = zmed – zmin
A2 = zmed – zmax
如果 A1 > 0 且 A2 < 0, 转到B层,否则增大窗口尺寸
如果窗口尺寸≤Smax,则重复A层,否则输出zxy
B 层:B1 = zxy – zmin
B2 = zxy – zmax
如果B1 > 0 且 B2 < 0, 输出zxy,否则输出zmed
中值滤波器的目的:除去“椒盐”噪声;平滑其他非冲激脉冲;并减少诸如物体边界细化或粗化等失真
2.4.3 混合滤波提高效率
结合快速滤波器(特别是线性滤波器)和排序统计滤波器(中值滤波器是个典型),使组合后的滤波器在效果上接近所期望的要求,但在计算复杂度方面有较大改进。
在线性和中值混合滤波中,常使较少的线性滤波操作作用在大的模板上,而线性滤波器输出的中值就是混合滤波器的最终输出。
![]()
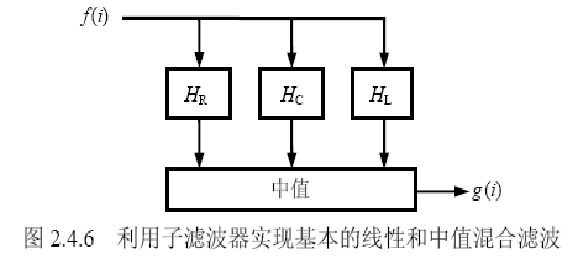
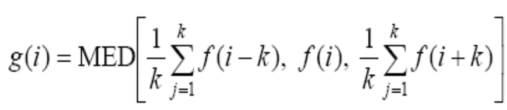
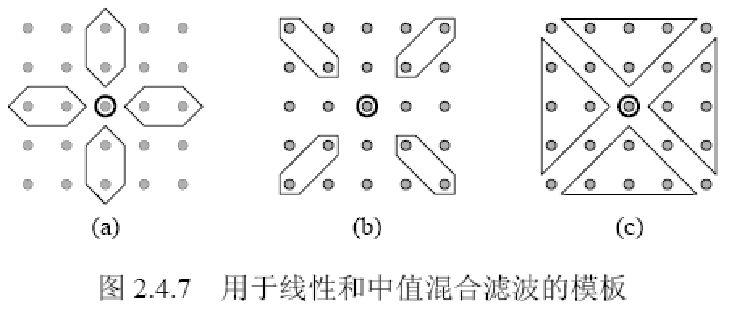
1、组合滤波器
线性滤波器消除高斯噪声,中值滤波器消除椒盐噪声。
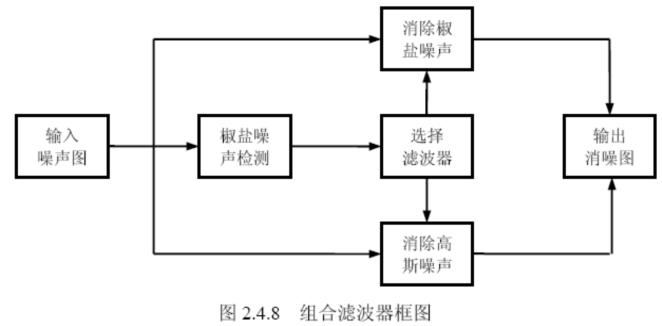
2、椒盐噪声检测器
受椒盐噪声影响的像素的灰度值会取到图像灰度范围的两个极端值,可用以下准则判断:
(1) 灰度范围准则
设图像灰度范围为[Lmin, Lmax],则不在 [Lmin+Tg, Lmax - Tg]范围中的像素为疑似噪声点
(2) 局部差别准则
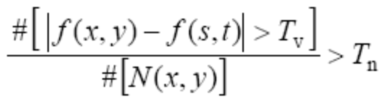
2.4.5 变换域滤波
频域滤波:噪声表现为高频,采用低通滤波去噪
小波域滤波:噪声对应的小波系数其幅值偏小,可以通过阈值方法去掉噪声的小波系数进行去噪
张量分解滤波:噪声表现为棒形分量小


