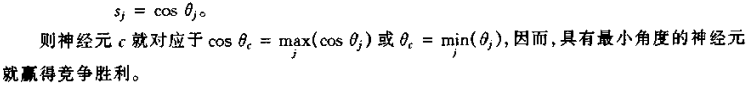《人工神经网络》第6章 自组织神经网络
自组织神经网络是一类无教师学习的神经网络模型，这类模型大都采用了竞争学习机制。自组织神经网络无需提供教师信号，它可以对外界未知环境（或样本空间）进行学习或模拟，并对自身的网络结构进行适当的调整，这就是所谓自组织的由来。
竞争学习机制以及自组织神经网络的代表模型：ART 模型、SOM 模型、CPN 模型
6.1 竞争型学习
竞争学习是指同一层神经元层次上的各个神经相互之间进行竞争，胜利的神经元修改与其相连的连接权值。这种机制可用来模式分类。竞争学习是无监督学习。在无监督学习中，只向网络提供一些学习样本，没有期望输出。网络根据输入样本进行自组织，并将其划分到相应的模式类别中。
基本的竞争学习网络由两个层次组成，输入层次和竞争层次。竞争层次中，神经元之间相互竞争，最终只有一个或者几个神经元活跃，以适应当前的输入样本。竞争胜利的神经元就代表着当前输入样本的分类模式。
6.1.1 竞争学习原理
竞争学习网络第一层次是输入层次，接受输入样本。第二层次是竞争层次，对输入样本进行分类。这两个层次的神经元之间进行连接如图 6.1 所示。对于某个神经元 j 的所有连接权之和为 1，即
6.1.2 竞争学习网络特征
在竞争学习中，竞争层的神经元总是趋向于响应它所代表的某个特殊的样本模式，这样，输出神经元就变成检测不同模式的检测器。竞争学习方法，是网络通过极小化同一模式类里面的样本之间的距离，极大化不同模式类间的距离来寻找模式类。模式距离指 Hamming 距离，模式 010 与模式 101 的 Hamming 距离是3。
对这种竞争学习算法进行的模式分类，有时依赖于初始的权值以及输入样本的次序。
对比：竞争学习网络模式分类 VS 典型 BP 网络分类
BP 网络分类学习必须预先知道将给定的模式分为几类。竞争网络能将给定模式分成几类预先并不知道，只有在学习之后才能确定。
从模式映射能力来看，后面要介绍的 CPN 竞争网络，由于竞争层上仅有一个输出为 1 的获胜单元，所以不能得到某些映射所要求的复杂表示；而 BP 网络能够在最小均方意义上实现输入—输出映射的最优逼近。
局限：
首先，只有部分输入模式训练网络，当用一个明显不同的新的输入模式进行分类时，网络的分类能力可能会降低，甚至无法进行分类。这是因为竞争学习采用非推理方式调节权值。另外，竞争学习对模式变换不具备冗余性，其分类不是大小、位移和旋转不变的，竞争学习网络没有从结构上支持大小、位移和旋转不变的模式分类。从使用上，一般利用竞争学习的无监督性，将其包含在其他一些网络中，仅作为其中的一部分。
6.2 自适应共振理论 (ART) 模型
ART（Adaptive Resonance Theory）模型是一种自组织神经网络。ART 模型成功地解决了神经网络学习中的稳定性（固定某一分类集）与可塑性（调整网络固有参数的学习状态）的关系问题。
ART 是以认知和行为模式为基础的一种无教师、矢量聚类和竞争学习的算法。在数学上，ART 由线性微分方程描述；在网络结构上，ART 网络是全反馈结构，且各层节点具有不同的性质；ART 由分离的外部单元控制层间数据通讯。ART 与其他网络相比，具有以下特点：
（1）神经网络要实现的是实时学习，而不是离线学习。
（2）神经网络面对的是非平稳的、不可预测的非线性世界。
（3）神经网络具有自组织的功能，而不只是实现有教师的学习。
（4）神经网络具有自稳定性。
（5）神经网络能自行学习一种评价指标（评价函数），而不需要外界强行给出评价函数。
（6）神经网络能主动地将注意力集中于最有意义的特征，而不需要被动地由外界给出对各种特征的注意权值。
（7）神经网络能直接找到应激发的单元，而不需对整个存贮空间进行搜索。
（8）神经网络可以在近似匹配的基础上进一步学习，这种基于假设检验基础上的学习对噪音具有更好的鲁棒性。
（9）神经网络的学习可以先快后慢，避免系统振荡。
（10）神经网络可实现快速直接访问，识别速度与模式复杂性无关。
（11）神经网络可通过“警戒”参数来调整判别函数。
6.2.1 ART-1 的基本原理
ART-1 的结构原理如图 6.4 所示。模型被分为两个子系统，子系统和取向子系统。
子系统处理已学习的模式，也就是对已经熟悉的模式建立起精确的内部表示；取向子系统处理新出现的模式，当不熟悉的事件出现时，它回调注意子系统，在内部建立新的内部编码来表示不熟悉的事件。
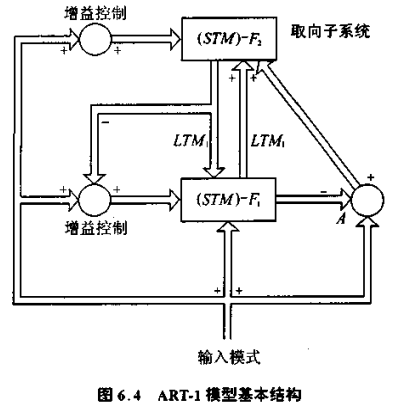
在注意子系统中有两个非几何意义上的层次来处理接收到的信息，即：F1 和 F2，短期记忆（ STM：Short Term Memory）。F1 和 F2 之间的连接通道
，为长期记忆（LTM：Long Term Memory）。该长期记忆又分为自上而下和自下而上两类，它们都用相应的权值来表示。子系统中的增益控制使得 F1 可以对自下而上的引发模式和自下而上的输入模式加以区分。
（1）ART-1 的工作过程
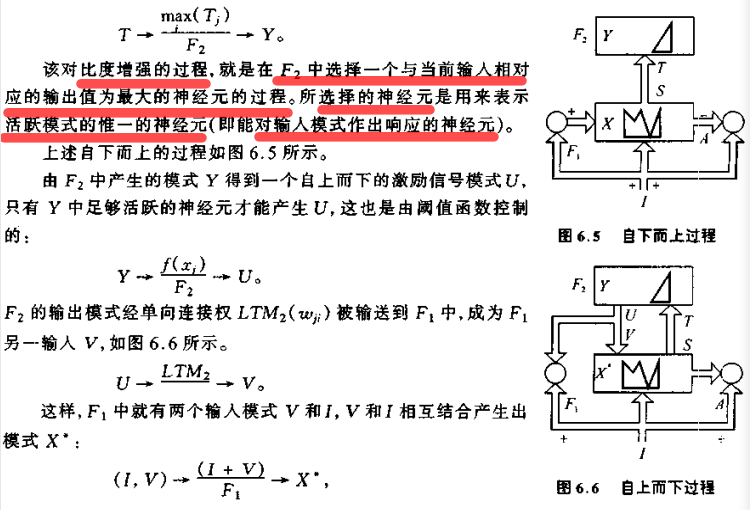X* 与仅由 I 产生的 X 是不同的。特别的，F1 要进行 V 和 I 之间的匹配，匹配结果用来确定进一步的学习和作用过程。
通过上述过程可知，信号模式在 F1 和 F2 之间来回运行（振荡），不断调整 V* 与 I，直至与其匹配（共振）为止。
对于调整子系统的激励作用可以这样考虑：
（2）2/3 匹配原则
模式 V 和 I 匹配是根据一定规则进行的。该规则称为 2/3 匹配规则，这是根据 F1 可能的 3 个输入信号（自上而下的样板 V、自下而上的输入模式 I、增益控制输入）中要是有 2 个起作用才能使 F1 产生输出而命名。F1 中的神经元是否被激活，依赖于足够大的自上而下和自下而上信号的共同作用。只接受两个信号中的一个，神经元节点就不会起作用，所以失配部分不会被激活，如图 6.9(c)。图 6.9(d) 表示模式之间的抑制连接，注意当子系统从一个模式向另一个模式移动时，这种抑制可以阻止 F1 提前发生激活。
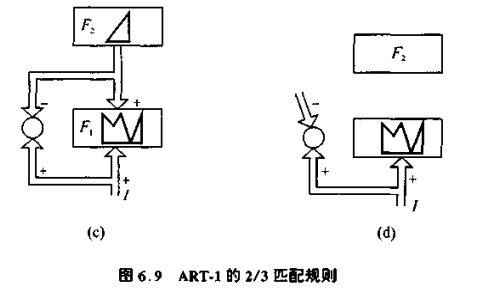
增益控制可以决定 F1 如何知道信号来自下边的输入还是来自上边的反馈。因为当 F2 被激发，启动向 F1 输送学习样板时，增益控制就会给出抑制作用来影响 F1 对输入响应的灵敏度，从而使得 F1 区分自上而下和自下而上的信号。
6.2.2 ART-1 的学习算法
这是一种快速学习算法，而且是边学习边运行，输出节点中每次最多只有一个为 1。每个输出节点可以看成一类相似样本的代表。由第 7 步修改权值可知，一个输出节点从上至下的所有权值对应于一个模式，当输入样本距离一个这样样本模式较近时，代表它的输出节点被激活。通过警戒线的调节可调整模式的类数：ρ 小，模式类别少；ρ 大，模式类别多。
6.2.3 ART-2 模型
ART-2 的功能结构与 ART-1 大体相似，基本思想仍采用竞争学习机制。ART-2 的输入可以是任意的模拟向量。在 ART-2 的模型中，F1 采用了一种三层结构。
实心圆点的功能是求输入向量的模。
图示 F1 中，第一层（底层）和第二层（中层）构成一个闭合的正反馈回路。其中，标记 Zi 的节点接受输入 Xi，而标记为 Vi 的节点接受上层送来的信号 bƒ(si)，回路中还包括两次规范化运算和一次非线性交换。
F1 的第二层（中层）个第三层（上层）构成另一个闭合正反馈回路，其中标记为 pi 的节点既接受中层送来的信号 ui，又接受 F2 送来的信号。回路中也包含两次规范化运算和一次非线性交换，在上层 si 进行的运算为：
重要结论：
1、当网络学习稳定后，如果将一个已学习过的模式提供给网络，那么该模式将正确的激活所在类别的 F2 单元，并且共振状态出现。这种“直接访问”特性意味着网络能迅速访问已存贮的模式。
2、学习过程是稳定的，即，网络对任何一个输入模式经过有限次学习后，能产生一组稳定的连接权向量。当这个输入模式重复提供给网络时，不会引起网络连接权无休止地循环调节。（只调节一次就会被网络记忆）
网络对任何一个输入模式，试图将它进行有类别的分类。如果分类不成功，则将它归入一个新的类别。不管分类成功与否，都将它存贮于网络之中。这个过程使网络边学习边回想，实现了在线学习的功能。进一步地，网络通过选择恰当的警戒参数，可对任意数目的输入模式按要求分类。
ART 网络很好地模拟了人类大脑记忆的“稳定性”和“可塑性”机理。但是，ART 模型却未能模拟“内部表示”的分布式存贮原理。在 ART 中，若 F2 中某一单元“损坏”，将导致该类别模式的信息全部丢失。（F2 中存贮的是类别模式的信息，一旦损坏，将会丢失信息）
6.3 自组织特征映射（SOM）模型
自组织特征映射模型也称为 Kohonen 网络。
SOM 由全互连的神经元阵列形成的无教师自组织学习网络。Kohonen 认为，处在空间中不同区域的神经元有着不同的分工，当一个神经网络接受外界输入模式时，将会分为不同的反应区域，各区域对输入模式具有不同的响应特征。
SOM 模型典型特征是：可以在一维或者二维的处理单元阵列上形成输入信号的特征拓扑分布，因此 SOM 模型具有抽取输入信号模式特征的能力。SOM 模型一般只包含一维阵列和二维阵列，但可推广到多维处理单元阵列中。
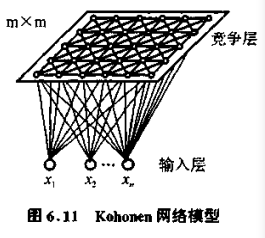
Kohonen 网络模型有四个部分：
（1）处理单元阵列：接受事件输入，并且形成对这些信号的“判别函数”。
（2）比较选择机制：比较判别“判别函数”并选择一个具有最大函数输出值的处理单元。
（3）局部互联作用：同时激励被选择的处理单元及其最邻近的处理单元。
（4）自适应过程：修正被激励的处理单元的参数，以增加其相应于特定输入“判别函数”的输出值。（增加2中那个最大函数输出值）
Kohonen 算法步骤：
对任意神经元 j，找到它的邻接神经元集合 Sj，根据时间来框取，时间越大，这个集合就越小，上图中 t2>t1>0；然后计算它们的 Euclidean 距离，最小或者最大，然后利用公式修改权值，计算输出。
6.4 CPN（Counter Propagation Networks）模型
CPN 通过组合 Kohonen 学习和 Grossberg 学习获得一种新的映射神经网络。CPN 也被称为重复传播模型，用来实现样本选择匹配，CPN 常被用作联想存贮、模式分类、函数逼近、统计分析、数据压缩等。
CPN 是一个三层前向网络，如图所示。各层之间全互连连接。隐含层称为 Kohonen 层，即竞争层，采用无监督学习规则进行学习。输出层称为 Grossberg 层，与隐含层全互联，但不进行竞争。Grossberg 层采用 δ 规则或 Grossberg 规则进行学习。
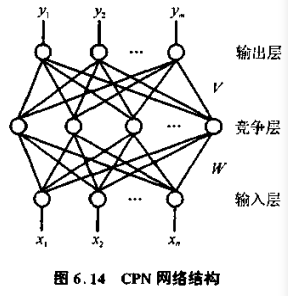
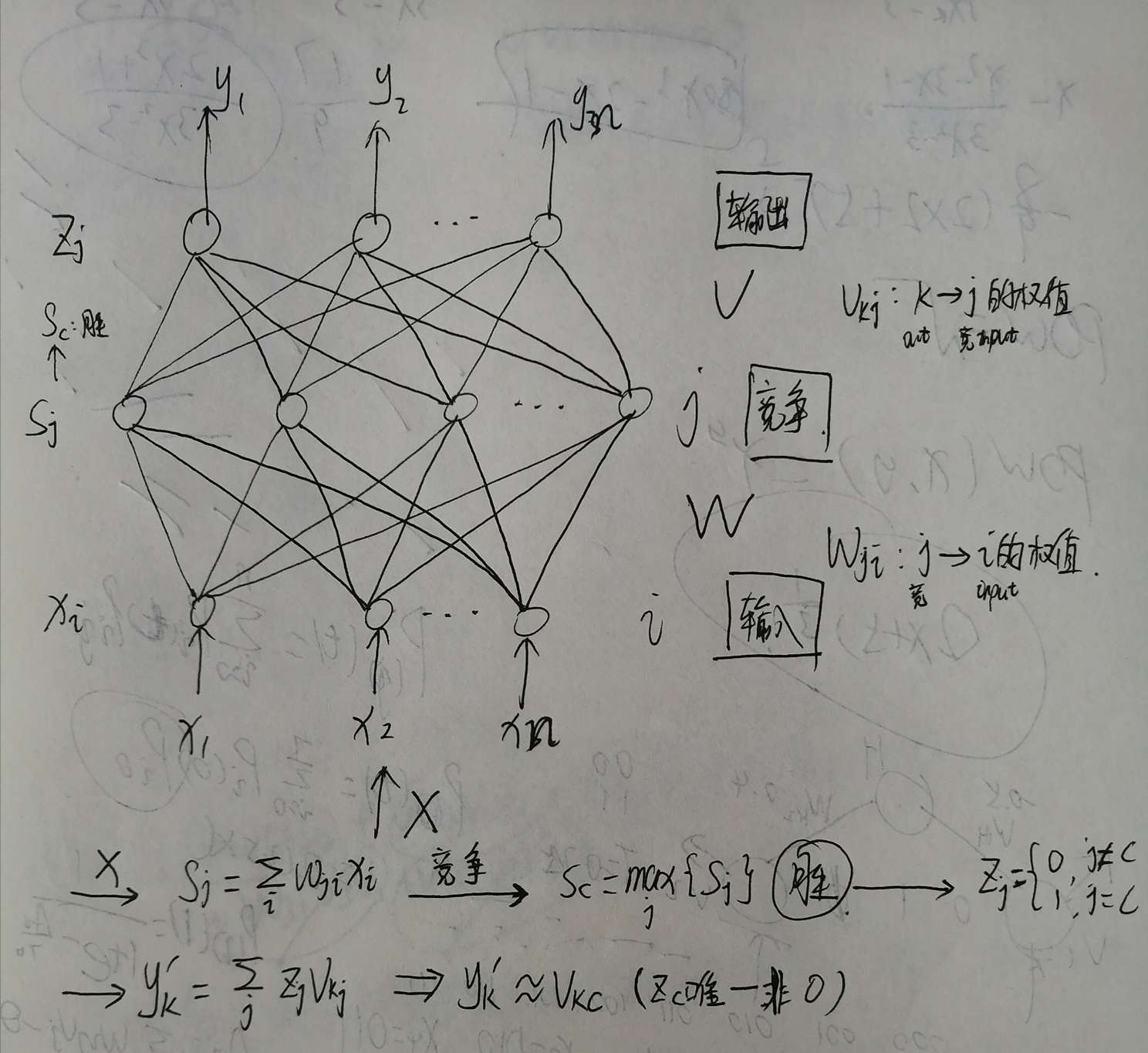
谁竞争胜利谁就会被输出。
CPN 的学习过程：
在学习期间对 Wj 和 Vk 进行调整，分别使用两种不同的算法。首先，当赢得竞争胜利的神经元 c 确定后，这一神经元 c 就被选择用来表达相应的输入样本。仅仅是连接到神经元 c 的从输入层到竞争层的连接权值被调整（Wji），其他的权值保持不变。竞争结束后，开始计算网络的输出，并将其与理想输出相比较，然后改变隐含层与输出层神经之间的连接权值。（总结：竞争胜利改变与神经元 c 连接的权值 Wij，输入到竞争，其他的权值不变；输出 y 时，与期望比较，改变其他的权值）
