《人工神经网络》第3章 EBP网络

EBP（Error Back Propagation）算法，简称BP

用BP算法的多层神经网络模型称为BP网络。拓扑如下：

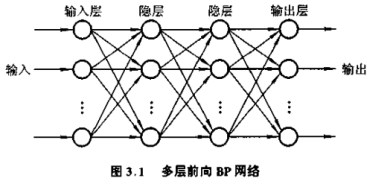
组成：输入层、中间层、输出层。中间层可有一或多隐层

学习过程：正向传播、反向传播

正向传播，输入信息从输入层经过隐含层处理后到输出层，每层神经元状态只影响下一层神经元状态。输出时误差过大，超出范围，转反向传播，误差信号沿原神经元连接通路返回，返回时，改变各层神经元连接权值，多次迭代，得到想要结果。

BP神经元激发函数：Sigmoid函数，一定阈值特性，连续可微

S型函数：

3.1 含隐层前馈网络δ学习规则

上章简单δ法则不适用，需推导一般δ法则

限制性说明：半线性函数（Quasi-linear Function）连续可微、单一类型输入、非递减函数，如上Sigmoid函数 f（x）

实际就是中间任意层其中一个神经元，当前的输入是上一层的输出并乘上权值的累加，当前的输出就是再经过f（•）处理，传向下一层

　　训练指标函数实质是求实际输出与期望输出的差值（类似求方差）；Δ_kw_ji是权值变化量，δ_kj训练误差，其实是中间一个过渡值，桥梁；求误差从输出层往前推，也就是反向；反向传播算法要求神经网络单元输入输出函数必须是可微。

　　若多层网络输入输出函数均为可导线性函数，网络失去非线性映射能力，原因是单层线性网络与多层线性网络是等价的。

BP算法把一组样本的输入/输出问题变为一个线性优化问题，使用优化中最简单的梯度下降法。

三层：输入，中间，输出；中间层的隐层数可以是任意的

LMS算法均方差函数只有一个极小点（全局最小点），但梯度下降法有多个极小点（局部极小点），不能保证求出全局最小点。

3.2 Sigmoid激发函数下BP算法

把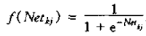求导之后带入到上面的式子３.５和３.６得到

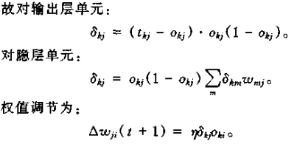
学习速率 η 对学习过程影响很大，η 是按梯度搜索的步长。η 越大，权值变化越剧烈。实际中，在不导致震荡的情况下取尽量大的 η 值。为了学习速度够快又不易产生振荡，在 δ 规则中加入了“势态项”：

α 是常数，决定过去权重的变化对目前权值变化的影响程度

BP模型不足：非线性优化，不可避免存在局部最小点；学习算法收敛速度很慢；隐层数选择带有盲目性经验性，无理论指导；新加入样本影响已学完样本

3.3 BP网络的训练与测试

3.3.1 误差曲线

网络收敛的好坏：速度、均方根误差

均方根误差：

m：训练集样本数；n：网络输出单元数

按照梯度法，BP网络在学习时，均方根误差应该逐渐减小。

如上图，有一段时间，误差随迭代次数的增加而保持不变，过了这段时间，误差又会快速减小，这种现象称为假饱和现象。这与网络的初始值设置、权值的修正量、样本的分布等因素有关。

　　初始权值一般在一定范围内按均匀分布随机产生的较小的随机值。在初始权值下，对于给定的输入模式，输出层总输入与阈值相差很大，此时该单元进入工作饱和区，也就是Sigmoid触发函数处于较平稳区间。在饱和区，要对权值有较大的修正才能尽快出去。但是，此时触发函数导数值小，每次学习对权值的修正很小，会保持一段时间在饱和区，网络的均方根误差保持不变或变化很小，造成假饱和现象。

3.3.2 泛化性能测试

训练集和测试集都由输入——输出样本对构成，来源同一数据集合。

训练集：训练网络，使网络按学习算法调节结构参数，以达到训练目的

测试集：评价已训练好网络的好坏，即网络泛化性能

训练集的数据只是数据集合的一部分，并不能保证其他样本也能有好的结果

用除去训练集的数据组成测试集，若结果满意，则网络的泛化能力强，否则就是训练样本没有代表性，不能体现源数据集的整体特征，泛化能力弱或很差

为了获得较好的网络性能，前提：训练集和测试集应使用经典样本对；测试集应不同于训练集

3.4 BP算法的改进

3.4.1 Vogl快速算法

BP算法收敛速度慢，Vogl提出“批处理”思想：每一个输入样本对网络不是立即产生作用，而是全部输入样本到齐，将全部误差求和累加，集中修改一次权值，根据总误差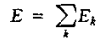

按式修改权值且有，

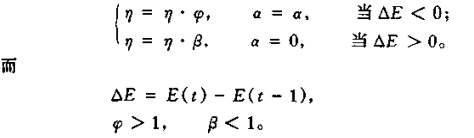
Vogl 的改进：1、降低了权值的修改频率，使权值沿总体误差最小的方向调整，避免走回头路

2、根据学习情况确定学习速率，让学习速率 η 和动量项 α 可变；若当前误差梯度修正方向正确，就增大学习速率，加入动量项，否则减小学习速率，去掉动量项，从而使学习速率大大提高。如上述花括号公式所示。

为了避免整体学习速率过大出现计算溢出，做出如下修正：

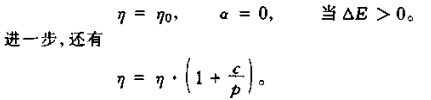
其中，c为常数，p是学习周期数

上述修正可以在一定程度上避免Vogl算法因学习速率过大导致学习过程出现振荡。

3.4.2 二阶BP算法

　　传统BP网络由一阶神经元级联而成，一阶神经元只能获取输入数据与输出之间的一阶相关信息，所以在进行高维输入模式的数据分类与识别时，需要大量的隐层节点来建立输入与输出之间的映射，增加了训练时间，有时因为局部极小而不收敛。故引入高阶BP网络。

节点响应为：

3.4.3 二阶快速BP算法

该算法对上述式（3.31）中学习速率 η 进行调整，即为

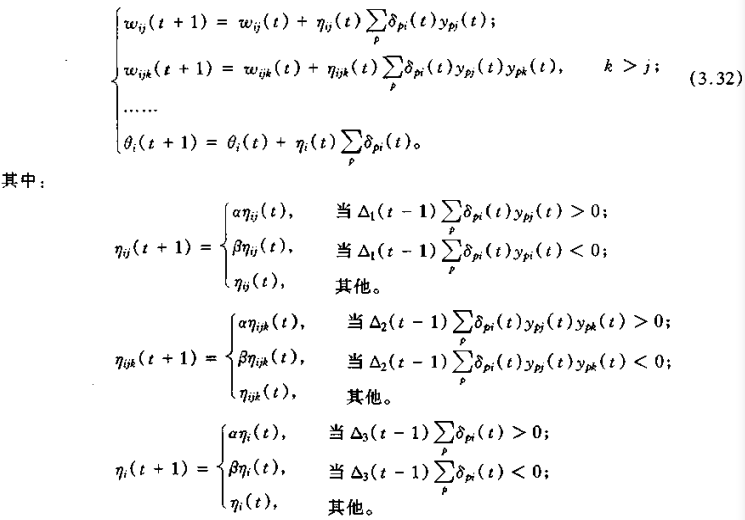
式中，

二阶快速BP算法步骤：

（1）预置参数 α，β，γ，η_ij(0)，η_ijk(0)，η_i(0)，将权值和节点阈值在 [-1,1] 区间随机初始化

（2）给定希望的输出和收敛准则 ε

（3）t = 0

（4）在 t 时刻，输入所有训练模式集，并计算响应 y_pi(t)

（5）按式 (3.32) 计算网络在 t 时刻总的误差 E(t)

（6）判定是否 E(t) ≤ ε ，如果是，转到（9），否则，转到（7）

（7）按式 (3.32) 进行权值调节

（8）t = t + 1 ,并转向（4）

（9）存贮权值和阈值参数，结束

3.4.4 动态自适应BP网络模型及其快速算法

BP网络模型的缺点：学习效率不高

原因：神经网络信息处理能力不仅取决于神经元之间的联接强度，与网络的拓扑结构也有关。典型的BP网络是一个冗余结构，它的结构和隐层节点数目受人为影响较大，认为确定之后，不能在学习过程中自主变更。节点数少，学习过程不收敛，节点多，网络的学习及推理效率变差，性能下降。

动态自适应BP网络模型及快速算法可以使BP网络能自动调节隐层节点数

算法核心：在保证网络能将 Rⁿ空间的一个连续子集连续映射到 R^m空间的前提下，尽量压缩中间层隐节点单元，以达到提高学习效率的目的。