OO第三阶段作业总结

一、JML语言的理论基础与应用工具链

1.理论基础

JML（Java Modeling Language）是一种规格化设计的语言，它为程序猿之间的交流提供了一种能规避二义性的通用规范。对于代码设计而言，规格化设计提供了严密的设计逻辑描述；对于代码扩展而言，规格化提高了代码的可维护性。

2.应用工具链

　　使用openjml可进行规格检查。其中，-check选项检查JML语法规范，-esc选项对代码进行静态检查，-rac选项为动态检查。

二、SMT Solver的简单尝试

1.使用-check进行JML语法检查

检查对象：本单元第一次作业。

命令行输入：

java -jar D:\openjml-0.8.42\openjml.jar -encoding UTF-8 -cp C:\Users\philis\IdeaProjects\path\specs-homework-1-1.1-raw-jar-with-dependencies.jar -check C:\Users\philis\IdeaProjects\path-save\src\path\*.java

检测结果举例：

①子类重写父类方法时，其规格前应加上also，表示对父类规格的扩展。 

C:\Users\philis\IdeaProjects\path-save\src\path\MyPath.java:27: 警告: Method size overrides parent class methods and so its specification should begin with 'also'
    //@ ensures \result == nodes.length;

②调用非纯粹查询方法。

C:\Users\philis\IdeaProjects\path-save\src\path\MyPathContainer.java:70: 警告: A non-pure method is being called where it is not permitted: com.oocourse.specs1.models.Path.isValid()
      @ requires path != null && path.isValid() && containsPath(path);

③\old在requires中的使用。

C:\Users\philis\IdeaProjects\path-save\src\path\MyPathContainer.java:128: 错误: A \old token with no label may not be present in a requires clause
      @ requires path != null && path.isValid() && \old(containsPath(path));

2.使用-esc进行静态检查

       由于作业中的MyPath和MyPathContainer方法较为复杂，且存在ArrayList等难以进行JML检测的因素，故使用如下简单的除法类代码进行测试。

public class Divide {
    //@ requires b != 0;
    //@ ensures \result == a/b;
    public static double divide(int a,int b){
        return a/b;
    }
    public static void main(String[] args){
        System.out.println(divide(3,2));
        System.out.println(divide(2,0));
    }
}

命令行输入及其检测结果：

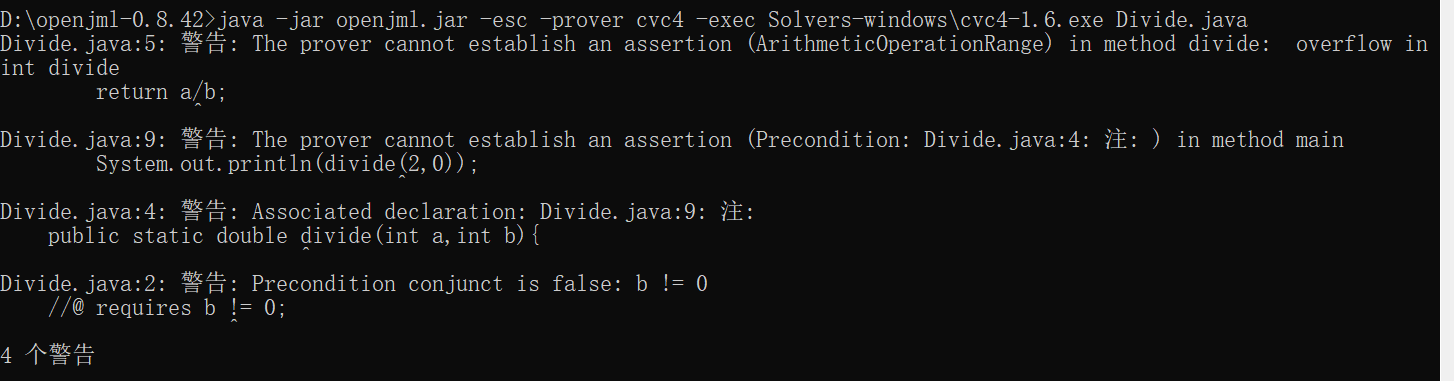
　　静态检查共4个警告信息。算术溢出是由于未将int型转为double型，前提条件错误则是因为divide(2,0)未满足divide方法的前提条件，即其requires。由此可见，静态检查能使程序猿提前知道运行代码时可能出现的错误及其实现与规格不符的地方，便于查错。

3.使用-rac进行动态检查

　　测试代码同（2）。

 

　　由图上的输出结果及异常可知，动态检查真正运行了程序。警告信息为运行时发现的divide(2,0)中实现与前提不符的问题。

三、部署JMLUnitNG自动生成测试用例

（1）MyPath测试

命令行输入：

java -jar jmlunitng.jar -cp specs-homework-2-1.2-raw-jar-with-dependencies.jar graph\MyPath.java
javac -cp jmlunitng.jar;specs-homework-2-1.2-raw-jar-with-dependencies.jar graph\*.java
java -jar openjml.jar -cp specs-homework-2-1.2-raw-jar-with-dependencies.jar -rac graph\MyPath.java
java -cp jmlunitng.jar;specs-homework-2-1.2-raw-jar-with-dependencies.jar graph.MyPath_JML_Test

文件树：

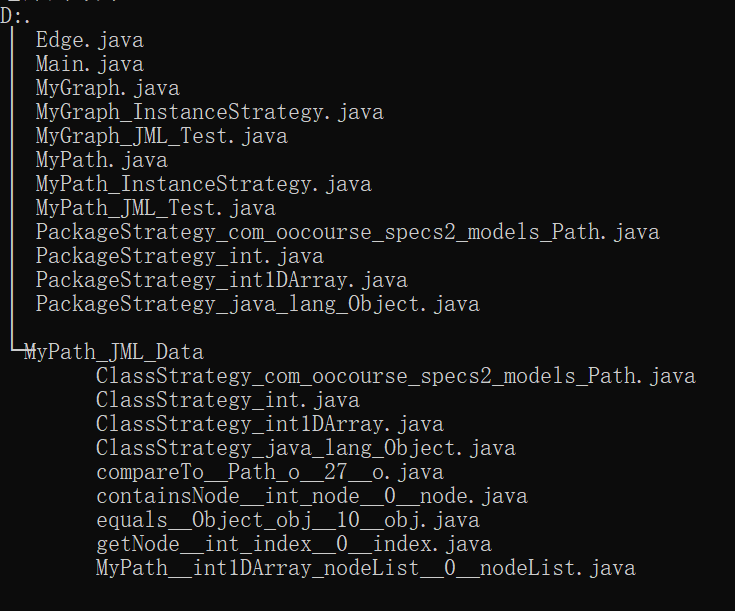
 运行结果：

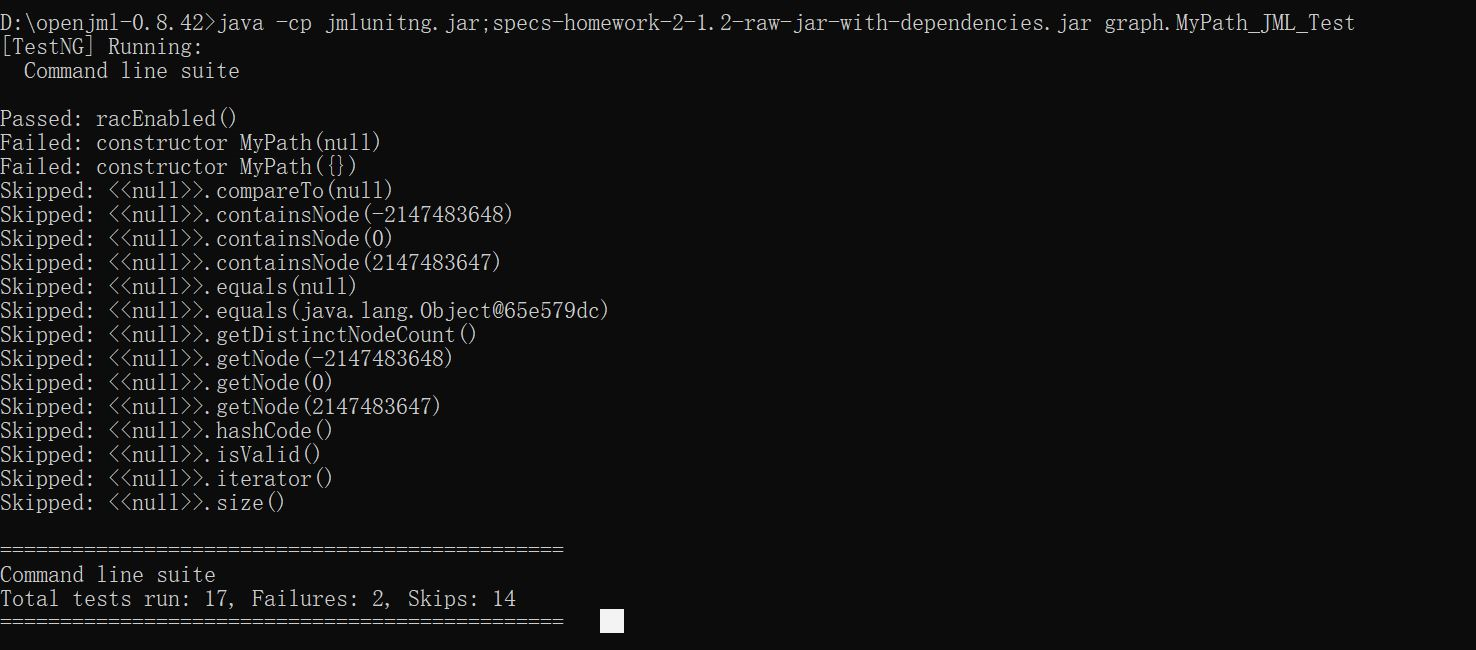
　　可以看出，JMLUnitNG主要进行边界条件的测试。对于MyPath类，其使用了空数组以及null进行测试。而对于这两种情况，构造函数均不能正确地建立Path，所以后面的测试只能全部Skip。

（2）MyGraph类测试

命令行输入：

java -jar jmlunitng.jar -cp specs-homework-2-1.2-raw-jar-with-dependencies.jar graph\MyGraph.java
javac -cp jmlunitng.jar;specs-homework-2-1.2-raw-jar-with-dependencies.jar graph\*.java
java -jar openjml.jar -cp specs-homework-2-1.2-raw-jar-with-dependencies.jar -rac graph\MyGraph.java
java -cp jmlunitng.jar;specs-homework-2-1.2-raw-jar-with-dependencies.jar graph.MyGraph_JML_Test

　　由于下面的这个错误，racEnabled()这一步实际上是failed了（实在研究不出来这是什么毛病了emmm，还请各位大佬告知orz），但是下面的检测也还能跑出来，所以运行结果就一并贴上了。

文件树：

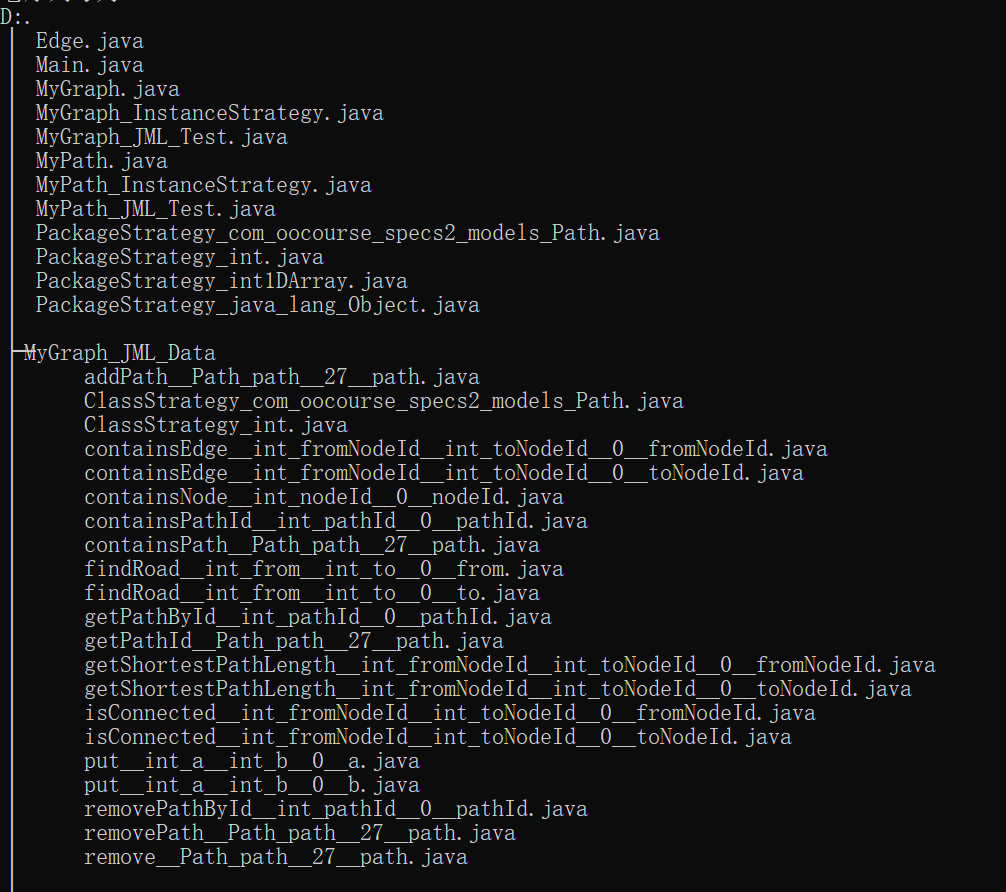
运行结果：

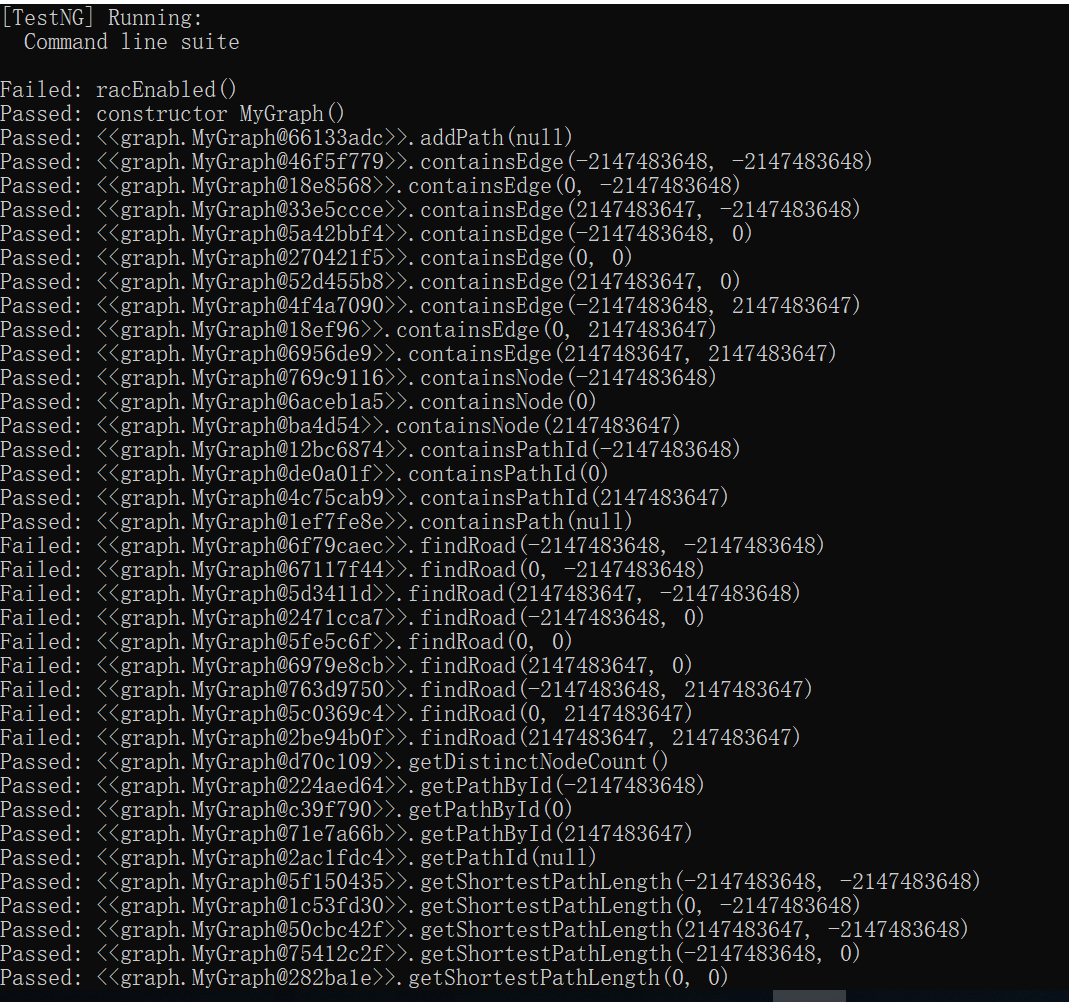
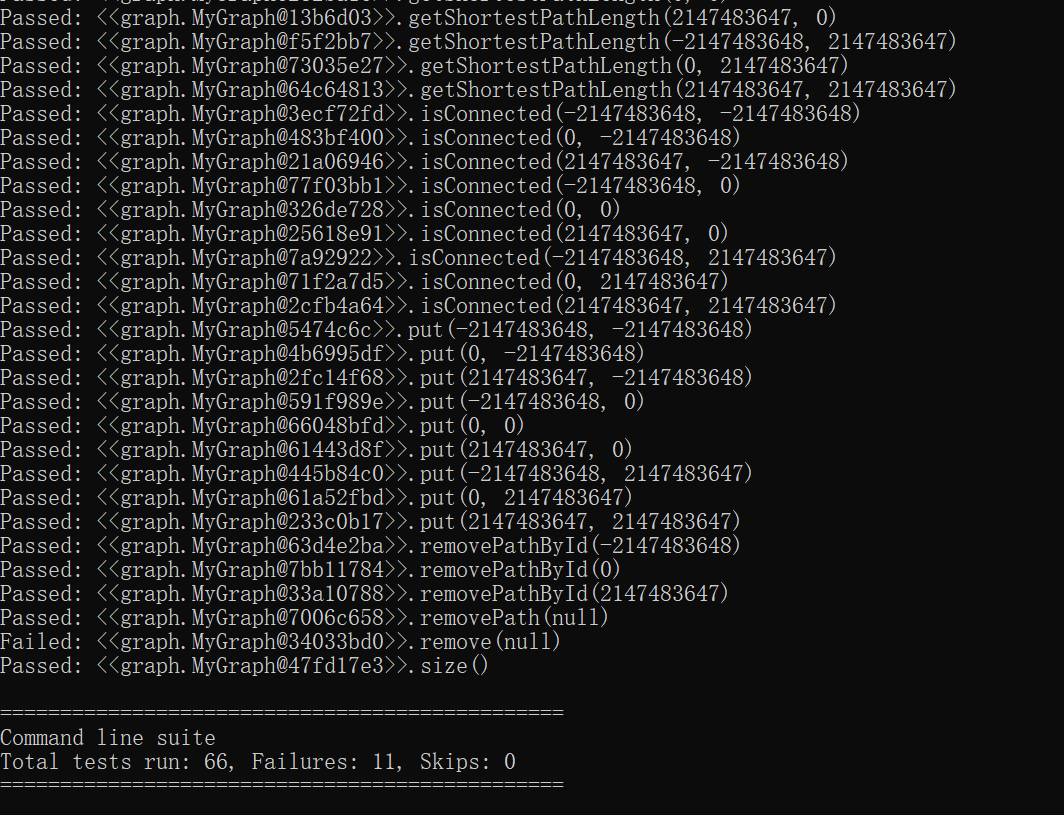
　　同样可以看出，测试主要围绕着int型范围的边界以及null展开。（然而这个findRoad实在failed得很迷。。。）

四、架构设计与迭代中的重构

第一次作业

（1）基本思路

　　本次作业中构建了MyPath和MyPathContainer两个类。MyPath类主要用于构建与存储路径，MyPathContainer则实现路径及结点的增删改查。这次作业的架构实现较为简单，难点在于复杂度的把握。由于增删指令较少而查询指令较多，故采用构建三个HashMap，即mapPathId，mapIdPath及mapNodeNum的方式，以增加增删操作复杂度及增加空间开销的方式，利用HashMap按键值查询复杂度O(1)的优势，降低查询操作的复杂度，控制运行时间。

（2）类图

第二次作业

（1）基本思路

　　本次作业把MyPathContainer类扩展成MyGraph类，增加了统计边数、判断结点是否连通及计算结点间最短路的功能，难点仍在于复杂度的把握。为实现新增功能，在架构中增加了类Edge以表示边，并在MyGraph类中增加mapNodeConnect，mapEdgeNum和mapEdgeDis三个HashMap。其中，mapNodeConnect相当于邻接表，存储Path上各点的连边情况；mapEdgeNum记录每条边的数目，以降低containsEdge查询的复杂度；mapEdgeDis用于缓存中间结果。需要注意的是，每次addPath和removePath时若存在对于边的增删，则需要清空缓存，避免查询错误。

　　判断结点是否连通及计算最短路均使用广度优先搜索算法，从起点出发，若到达终点，则直接break出来；否则继续寻找，直到某一层寻找到的临界点总数为0，从而判断出起点与终点不连通为止。沿途中得到的最短路长度都缓存在mapEdgeDis中，这样能在查询指令较多时直接以O(1)的复杂度得到结果。

（2）类图

第三次作业

（1）基本思路

 　　本次作业将MyGraph类扩展成MyRailwaySystem类，主要新增功能有查询连通块数、计算最低票价、最少换乘次数和最少不满意度。将查询连通块数、判断是否连通及计算最短路归为一类，都用bfs解决。考虑到增删指令极少而查询指令很多，故在每个addPath和removePath后跑一遍bfs对连通的点染上相同的颜色，解决此后所有查询连通块和判断连通的指令。对于最低票价、最少换乘次数和最少不满意度，新建一个Graph类跑Dijkstra算法，并将中间结果缓存，每次增删边时清空缓存。同时，新增Node类和Dst类，分别把点的编号与路径编号，边的终点与权值作为整体，作为算法运行的基础，增加了数据存储的灵活性。

（2）类图

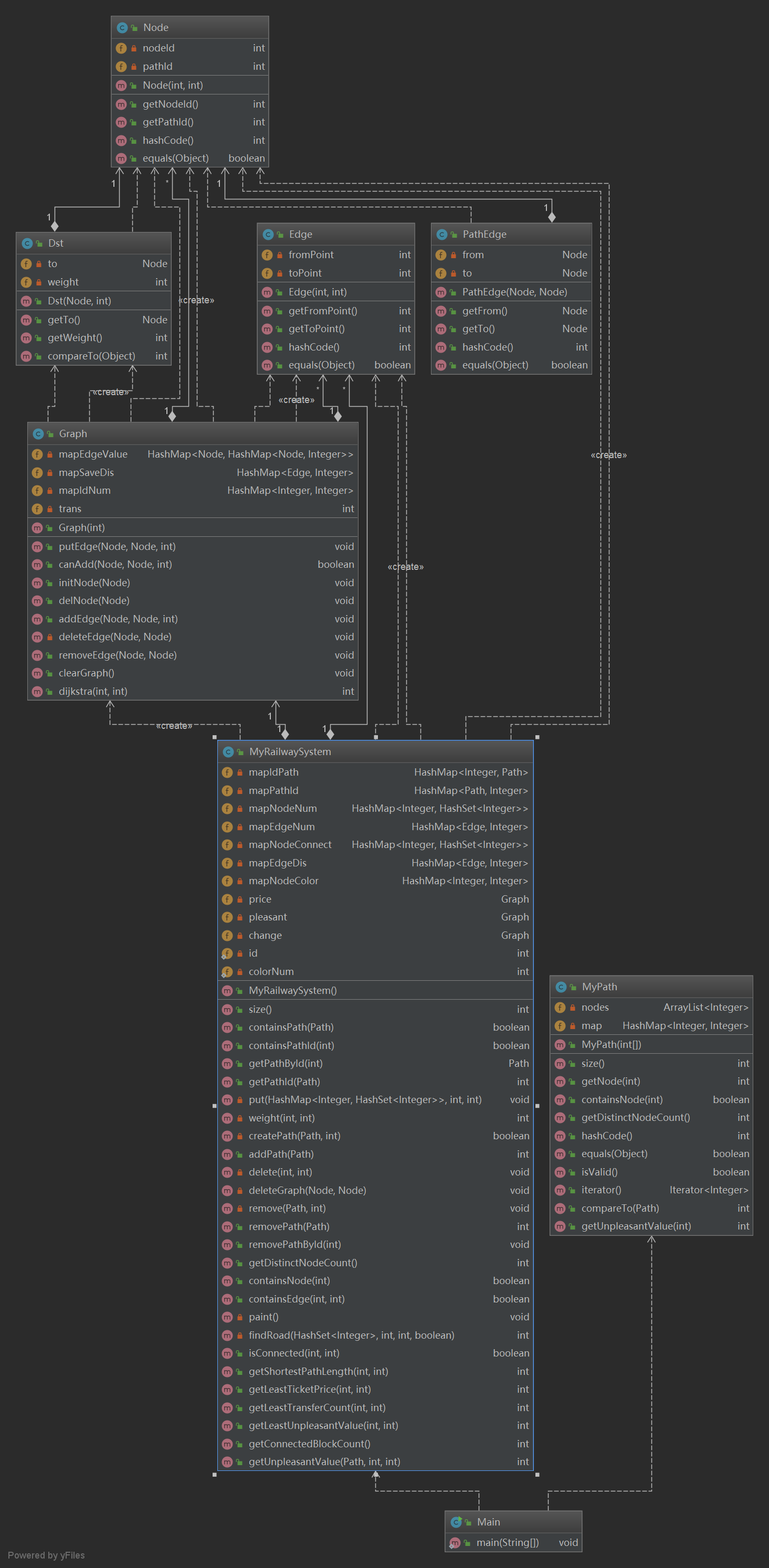
五、代码实现的bug和修复情况

第二次作业

　　出现了空指针错误的问题。原因是当出现Path为1 2 2 3，即有连续的两点相同时，会在作为邻接表的HashMap中将其删除两次。若第一次删除操作后，结点2对应的邻接表已经为空，则会直接remove这个key，因此，当第二次想删除key=2对应的邻接表中的2时，由于这个key已经不存在，从而出现空指针错误。

第三次作业

　　出现tle的问题。原因是在设计中采用了将不同路径上相同编号的结点两两连边的方式来建图。而由于Dijkstra算法的复杂度为ElogE，当不同路径有大量重复结点时，就很容易tle。解决方法是为每个存在于图中的结点编号增加两个pathid分别为0和-1的虚点作为起点和终点，相同编号的结点向起点连边，起点向终点连边且权值为换乘消耗，终点再向相同编号的实点连边，且这些边均为单向边。此时，就算出现大量path经过相同结点的情况，这一编号结点的连边数也仅为2*n+1而非n*(n-1)，大大减少了边数。

六、规格撰写和理解上的心得体会

　　规格化语言消除了自然语言可能存在的歧义，为编程人员提供了统一的规范。需要注意的是，规格的描述并不是对实现具体繁杂的规定，而是以简练的语言阐述requires，assignable，ensures，即方法的前提、可修改的数据及后置条件，并针对正常与异常行为给出一系列的规定。在三次作业中，可以发现相同的规格也能造就复杂度、架构甚至采用的数据结构都完全不同的代码实现，其原因就在于规定前因后果与规定实现过程是完全不同的两回事，这也正是面向对象和面向过程的差异所在。同时，规格也能利于单元测试的实现，从先写代码后debug转向边写代码边debug。事实上，我们在以前面向过程的程序设计中也常常在遇到bug时将后面的部分先注释掉，一部分一部分的调试，直到每一部分都能按照我们预想的行为运行为止，这也正是单元测试最朴素的实现。而规格化与单元测试只是为此提供了一个更加简便易用的实现方式。