matlab PID程序

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

%设一被控对象G(s)=50/(0.125s^2+7s)<em id="__mceDel">%用增量式PID控制算法编写仿真程序 %输入分别为单位阶跃、正弦信号，采样时间为1ms   clear; close all; ts=0.001;                 %采样时间 sys=tf(50,[0.125,7,0]); %tf是传递函数  即被控对象函数G（）; dsys=c2d(sys,ts,'z');    %把控制函数离散化 [num,den]=tfdata(dsys,'v');% 离散化后提取分子、分母 u_1=0; u_2=0; y_1=0; y_2=0; error_1=0; error_2=0; P=0;I=0;D=0; n=1000; time=zeros(1,n); rin=zeros(1,n); yout=zeros(1,n); for k=1:n     time(k)=k*ts;                   %采样时间     S=1;     if S==1         kp=10;ki=100;kd=0.1;        %初始化PID         rin(k)=1*(time(k)>0.1);     %Step Signal     elseif S==2         kp=10;ki=100;kd=0.1;         rin(k)=0.5*sin(2*pi*k*ts);  %Sine Signal即实际输入     end     du=kp*P+kd*I+ki*D;              %PID Controller控制系数     u=u_1+du;                       %Restricting the output of controller           yout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;   %实际输出     error=rin(k)-yout(k);           %Return of parameters 误差     u_2=u_1;                        %保存上上次输入     u_1=u;                          %保存上一次控制系数     y_2=y_1;                        %保存上上次输出     y_1=yout(k);                    %保存上一次输出     P=error-error_1;                %Calculating P     D=error-2*error_1+error_2;      %Calculating D     I=error;                        %Calculating I     error_2=error_1;                %保存上上次误差     error_1=error;                  %保存上一次误差 end figure; plot(time,rin,'b',time,yout,'r');   %输入和实际控制输出 xlabel('time(s)'),ylabel('rin,yout'); </em>

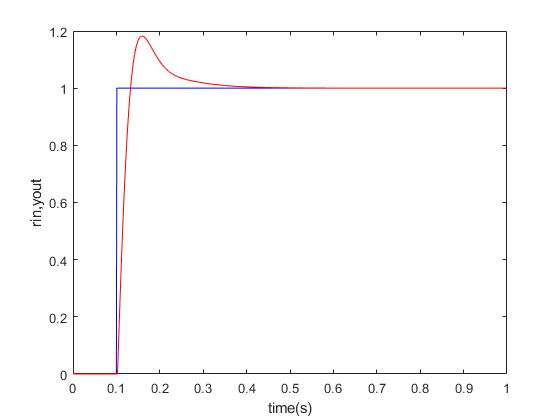
Simulink验证

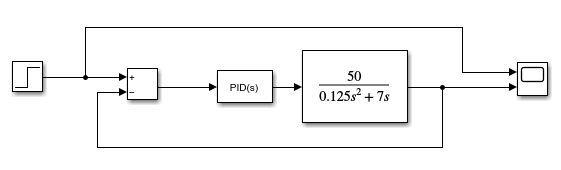
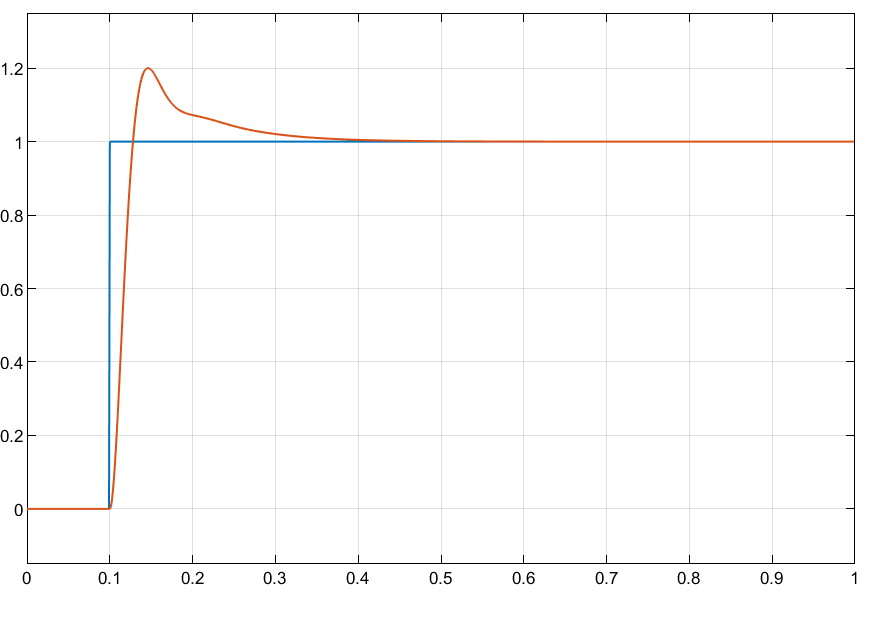
开环控制系统：被控对象的输出（被控制量）对控制器的输出没有影响。
闭环控制系统：被控对象的输出（被控制量）会反送回来影响控制器的输出。

在工程实际中，应用最为广泛的调节器控制规律为比例、积分、微分控制，简称PID控制。
当被控对象的结构和参数不能完全掌握，或得不到精确的数学模型时，控制理论的其它技术难以采用时，系统控制器的结构和参数必须依靠经验和现场调试来确定，这时应用PID控制技术最为方便。（PID控制可以应用于系统参数和特性不能被有效测量的场合。）

比例（P）：
控制器输出与输入误差信号成比例关系。
仅有比例控制时系统输出存在稳态误差。
积分（I）：
输出与输入误差信号的积分成正比关系。
比例+积分（PI）控制器，可以消除系统静差。
微分（D）：
控制器输出与输入误差信号的微分成正比关系。
具有比例+微分（PD）的控制器，能够提前使抑制误差的控制作用等于零，从而避免了被控量的严重超调，能改善系统在调节过程中的动态特性。