matlab近似泛函优化

泛函优化可以近似转化为各点坐标的优化。

如以下题目

用理论方式（欧拉方程）求解比较繁琐，门槛高，适应性差。当边界条件或目标函数发生变化时，需要新的理论。

该题目本质是求从(1,1)到(2,2)的最优路径曲线，使目标函数最小。因此可以转换为求解f(1.1)，f(1.2)，……，f(1.9)的最优取值，使目标函数最小。当各点取值得到优化后，也就是路径曲线得到了优化。

代码如下：

目标函数

function value=min_obj(x,t)
n=size(x,1);
value=ones(n,1);
for i=1:n
    x_i=[1,x(i,:),2];
    dx_i=diff(x_i);
    item=dx_i+dx_i.^2.*t(1:end-1).^2;
    value(i)=sum(item.*diff(t));
end
end

求解程序：

t=1:0.1:2;
f=@(x) min_obj(x,t);
x0 = 1.1:0.1:1.9;
A = [];
b = [];
Aeq=[];
beq=[];
lb=-10*ones(length(t)-2,1);
ub=10*ones(length(t)-2,1);
[x,fval] = fmincon(f,x0,A,b,Aeq,beq,lb,ub)
plot(t,[1,x,2]);
hold on;
plot(t,-2./t+3);
hold off;
xlabel('t');ylabel('x');
legend('Numerical analysis method', ...
    'Analytical calculation method');

得到结果对比如下：

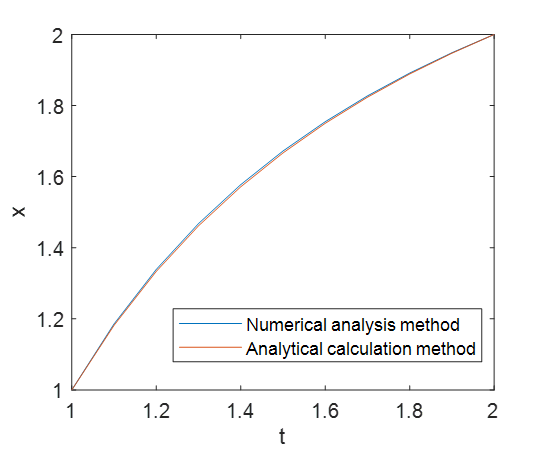
可以看到，数值方法的求解结果与理论解非常接近。误差也有一部分来源是目标函数的求导表达式不够精确。

该方法灵活方便，能应对多种问题形式。