过程选择模型
前段时间看到赵玉平老师讲的关于相亲选择的问题,感觉比较有趣,希望通过概率模拟验证一下该方法的有效性。
原链接如下,感兴趣可先了解原讲解:管理学博士是怎么硬核相亲的,过程太真实了,最后居然选到这么好的“对象”!强烈建议大家学学…… %相亲 https://v.douyin.com/RWQQnC4/
1.问题重述
1.1原问题描述
各位同学是我的媒人,每位同学为赵老师介绍一个男朋友,写下一个数字代表该男生的质量。每次见一个人,单方向不可重复。如决定要则结束,如决定不要则继续。
总结方法:先选4位同学(共12人)进行询问,记住其中的最大值,然后再从其他同学中询问,当得到大于前面所述最大值,则决定要。
1.2数学模型
现将原问题抽象为以下数学过程
- 随机生成n个数字;
- 将n个数字依次输入模型中,当决定选择其中某一个数字时(记为第k个,k<n)过程停止;
- 目标是使选出的数字尽可能大,尽可能在n个数字中排在前列。
策略是:
- 记n个数字的前a(a<n,a/n=r)个中的最大值为m;
- 从第a+1个数字开始,若小于等于第a个数则舍弃,若大于第a个数字则选择;
- 若直到最后一个数仍未出现大于第a个数的,则选择最后一个数。
该过程中存在这样一个问题:即这n个随机数服从什么分布。先假设其服从0到100之间的均分分布。
2.过程实现
设n=100,a=33,模拟如下。
import numpy as np
class choose:
def __init__(self,nums):
# nums代表提供的数字集
self.nums = nums
self.n=len(nums)
def get_max(self,a):
# 从前a个数中选出一个最大的,记为max_num
self.a = a
self.max_num = max(self.nums[0:a])
def decide(self):
self.flag = 0
for i in range(self.a,self.n):
# 如果遇到更大的数则选取
if self.nums[i]>self.max_num:
self.choice = self.nums[i]
self.flag = i
# 如全程未遇到更大的数则只能选择最后一个
if self.flag == 0:
self.choice = self.nums[self.n-1]
def show(self):
print('共有%d个数字,其中的最大值是%f,选择的数字是%f,排第%d位' %
(self.n, max(self.nums), self.choice, sum(c.nums>c.choice)+1))
if self.flag == 0:
print('在后续数字中未找到更大的,故最终在所有数字中选择了最后一个')
else:
print('选择了第%d个数字' % (self.flag+1))
n=100
a=33
nums=np.random.uniform(0, 100, size=n)
c=choose(nums)
c.get_max(a)
c.decide()
c.show()
模拟几次,结果如下:
共有100个数字,其中的最大值是96.647844,选择的数字是96.647844,排第1位 选择了第64个数字
共有100个数字,其中的最大值是99.571219,选择的数字是65.277241,排第31位 在后续数字中未找到更大的,故最终在所有数字中选择了最后一个
共有100个数字,其中的最大值是97.931539,选择的数字是41.759912,排第50位 在后续数字中未找到更大的,故最终在所有数字中选择了最后一个
共有100个数字,其中的最大值是99.566610,选择的数字是99.566610,排第1位 选择了第73个数字
共有100个数字,其中的最大值是98.271705,选择的数字是98.271705,排第1位 选择了第82个数字
可以发现,在5次模拟中有3次选到了全局最大,效果不错,但也有两次在后续数字中未找到更大的。
直接进行100000次模拟,观察情况:
choices = []
rank = []
fail = 0
for i in range(0,100000):
if i%1000==0:
print(i)
nums=np.random.uniform(0, 100, size=n)
c=choose(nums)
c.get_max(a)
c.decide()
choices.append(c.choice)
rank.append(sum(c.nums>c.choice)+1)
if c.flag == 0:
fail += 1
观察选出的数字的分布:
import matplotlib.pyplot as plt plt.hist(choices,100)
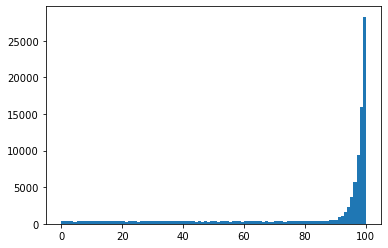
可以看到,大部分落在90~100之间,落在99~100之间的概率为0.28,效果较好,平均值np.mean(choices)=82.01201051783117。
观察选出的数字在原100个数字中的位次的分布:
plt.hist(rank,100)
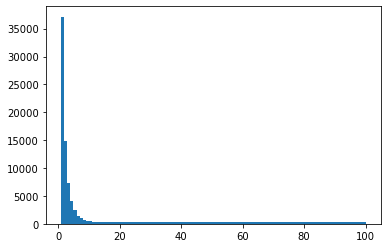
可以看到,大部分位次落在0~10之间,选到最大值(排第1位)的概率为0.37。平均值np.mean(rank)=18.16273,平均相对位次0.18。
3.敏感性分析
当参数发生变化时,该方法是否仍能有较好的效果。
3.1小样本
现实情况中我们的精力有限,往往没有那么多的选择机会,那么,当n减少时(a/n=r近似不变),会发生什么。
n=50,a=17。进行100000次模拟,平均位次10.10,平均相对位次0.20。
n=10,a=3。进行100000次模拟,平均位次3.03,平均相对位次0.30。
n=5,a=2。进行100000次模拟,平均位次2.2,平均相对位次0.44。
随着n的减小,能够取得的平均相对位次的变化情况如下图。
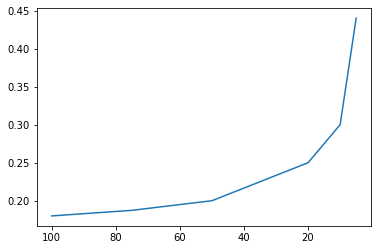
可见随着n的减小,该方法的效果变差,但由于样本少,该现象情有可原。
3.2策略值r
保持n=100不变,观察r的变化对结果的影响,对r从0.1到0.9取9个值,每个值模拟10000次。
n=100
rs=np.linspace(0.1, 0.9, 9)
m_choices=[]
m_rank=[]
m_fail=[]
for r in rs:
print(r)
a=int(round(n*r))
choices = []
rank = []
fail = 0
for i in range(0,10000):
nums=np.random.uniform(0, 100, size=n)
c=choose(nums)
c.get_max(a)
c.decide()
choices.append(c.choice)
rank.append(sum(c.nums>c.choice)+1)
if c.flag == 0:
fail += 1
m_choices.append(np.mean(choices))
m_rank.append(np.mean(rank))
m_fail.append(fail)
r对选择结果的影响:
plt.plot(rs,m_choices)
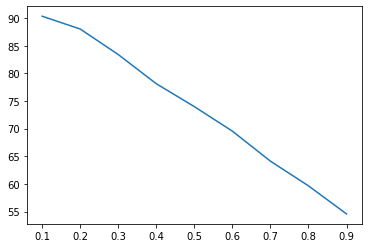
plt.plot(rs,m_fail)
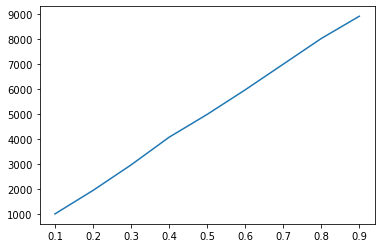
当r较大时,很容易在后续数字中找不到更大的,从而获得较差的最终选择。
n=10,观察r的变化对结果的影响,对r从0.1到0.9取9个值,每个值模拟10000次。
plt.plot(rs,m_choices)

plt.plot(rs,m_fail)
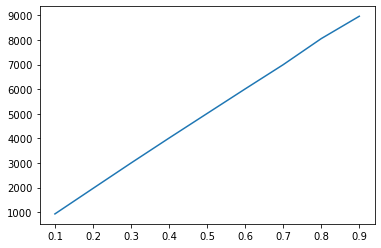
当n较小时,虽然随着r的增大,在后续数字中找不到更大的数字的概率也是近乎线性增大,但是如果a太小则选不到较大的阈值,因此r在0.1到0.9之间存在最优解。
这启示我们,当基数n较大时,r的取值可适当减小,以便获得更优的结果。
4.进一步讨论
可以看到,对于该方法,当在后续数字中找不到更大的数字时,只能被迫选择最后一个数字,导致结果较差。一个后续改进的思路是,当在一段时间内(第a个数字后的一些数字中)未发现更好的时,应适当降低要求。
对于不同的n,存在不同r的最优取值,n越大,r的最优取值越小。
如果原数据服从其他分布规律,如卡方分布,F分布等,则结果可能有不同的表现,可能需要根据不同的分布采取不同的策略。
实际上,回归相亲问题,现实情况远比该数学问题复杂的多,首先每个人有自己的特点,不能被很好地量化打分,即使打分也是各方面表现有不同的分数,其次,n是不可控的,且人的思维都是不断发展变化的,挑选者不可能一成不变地遵循一个死板的策略,被挑选者也不一定在被挑选后即接受。最后,且行且珍惜。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号