鱿鱼游戏玻璃桥模拟

鱿鱼游戏玻璃桥

18关，16人

各玩家遵守规则，依次前行。

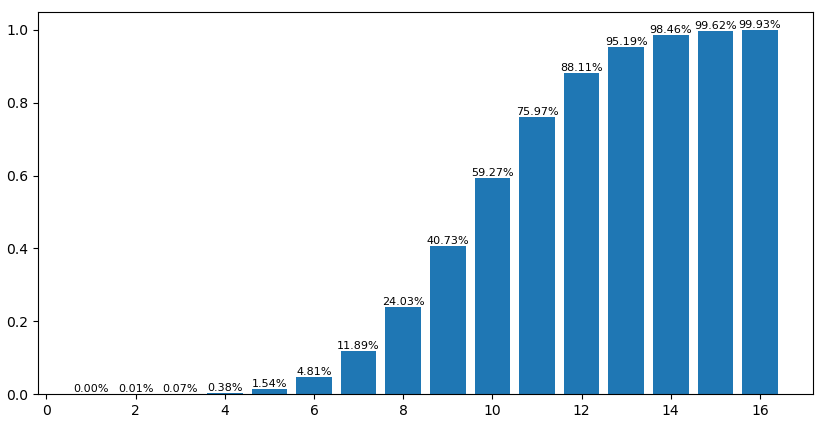
模拟各人存活概率。

import numpy as np

class gamer:
    def __init__(self):
        # 表示该游戏者已经走过了x块玻璃
        self.x = 0
    
    def choose(self):
        # 表示该游戏者做出选择，0表示选择左边，1表示选择右边
        self.choice = np.random.randint(0,2)
    
    def go(self,glass):
        for i in range(0,glass.n):
            if glass.walked[i]==1:
                self.x += 1
            else:
                glass.walked[i]=1
                self.choose()
                if self.choice==glass.which[i]:
                    self.x += 1
                else:
                    break
        self.final = self.x #该玩家最终通过了的玻璃数量
        return glass

class glass:
    def __init__(self,n):
        self.n = n
        # 生成n个0或1的随机数，0表示左边为安全的玻璃，1则表示右边
        self.which = np.random.randint(0,2,size=n)
        # 该序列表示每一块玻璃是否被走过，初始置0表示未被走过
        self.walked = np.zeros(n)

n=18
k=16

#%%
p = np.zeros(k)
sim = 1000000
for s in range(0,sim):
    if s%10000==0:
        print(s)
    g = glass(n)
    gamers = [gamer() for _ in range(0,k)]
    for i in range(0,k):
        g = gamers[i].go(g)
    for i in range(0,k):
        if gamers[i].final==n:
            p[i] += 1

import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.bar(range(1,k+1),p/sim)
for a,b in zip(range(1,k+1),p/sim):
    plt.text(a, b,'%.2f%%'%(b*100), ha = 'center',va = 'bottom',fontsize=8)
plt.show()

 

补充：直接计算方法

实际上除了概率模拟，对于该问题，也可以直接计算得到。每个玩家在各个位置掉落的概率与前一名玩家有关：

设第i个玩家在第j个玻璃掉落的概率为Pij
第1个玩家在第1个玻璃掉落的概率为P11=1/2，在第2个玻璃掉落的概率为P12=(1/2)^2……在第18个玻璃掉落的概率为P1,18=(1/2)^18，通关的概率也为(1/2)^18
第2个玩家在第1个玻璃掉落的概率为0，在第2个玻璃掉落的概率为P22=P11*(1/2)^(2-1)，在第3个玻璃掉落的概率为P23=P11*(1/2)^(3-1)+P12*(1/2)^(3-2)……

使用程序计算如下：

import numpy as np
n=18
k=16
p=np.zeros((k,n))
# 初始化第一位玩家的概率
p[0,]=np.logspace(1,n,num=n,base=0.5)

for i in range(1,k):
    for j in range(1,n):
        for b in range(0,j):
            p[i,j] += p[i-1,b]*(1/2)**(j-b)

import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.bar(range(1,k+1),1-p.sum(axis=1))
for a,b in zip(range(1,k+1),1-p.sum(axis=1)):
    plt.text(a, b,'%.2f%%'%(b*100), ha = 'center',va = 'bottom',fontsize=8)
plt.show()