电力电子Simulink仿真——PWM控制
1. 单相桥式
1.1 双极性
课本P165
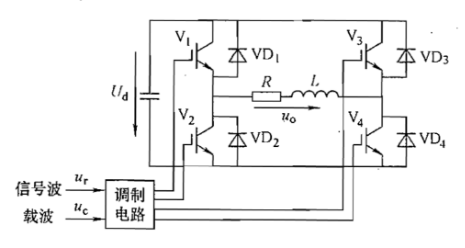
ur>uc时,V1和V4开通,V2和V3关断,此时如果io>0,则V1和V4通,如io<0,则VD1和VD4通,输出电压uo=Ud;
ur<uc时,V2和V3开通,V1和V4关断,此时如果io<0,则V2和V3通,如io>0,则VD2和VD3通,输出电压uo=-Ud。
模型;
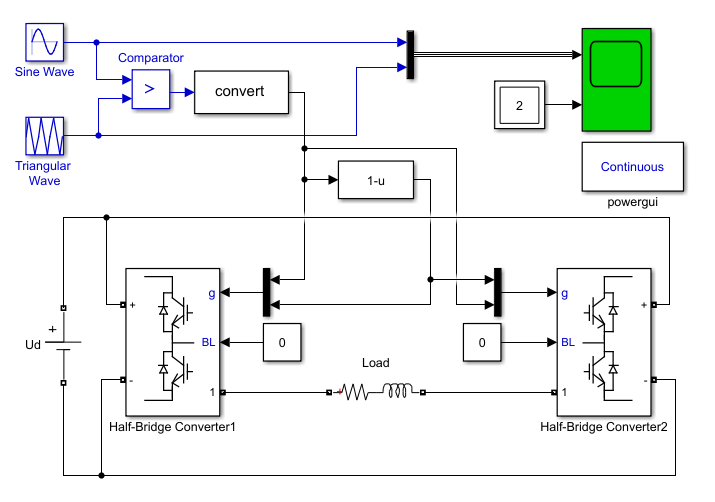
- 正弦波:频率50Hz,幅值0.8;
- 三角波频率:1000Hz;
- 输入电压:100V;
- 负载:1Ω,0.01H。
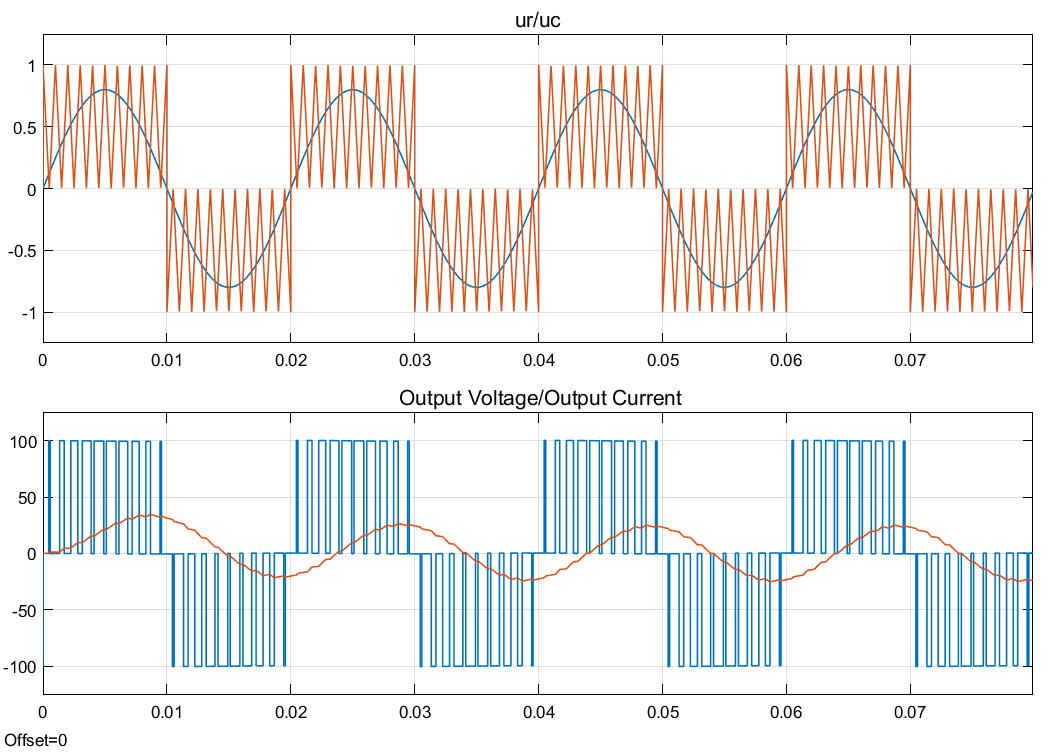
波形:
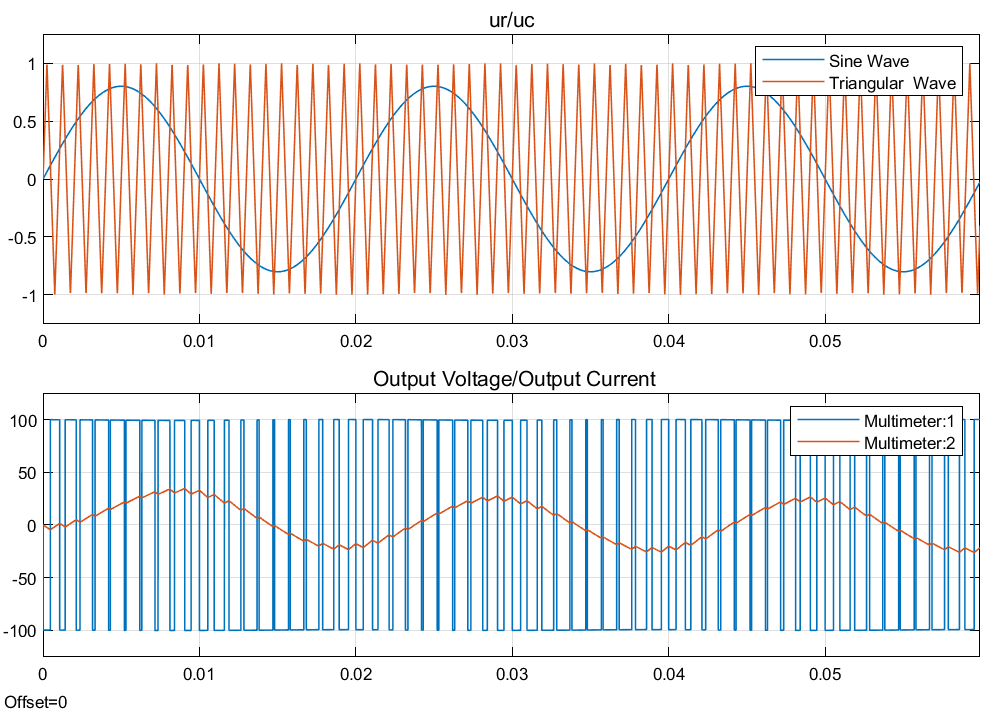
可以看到,输出电压在ur和uc的交点处翻转,输出电流为正弦波形,且滞后于信号波。
1.2 单极性
在输出电压uo的正半周,V1保持通态,V2保持断态,V3和V4交替通断。由于负载电流比电压滞后,因此在电压正半周,电流有一段为正,有一段为负。
在负载电流为正的区间,V1和V4导通时,负载电压等于Ud,V4关断时,负载电流通过V1和VD3续流,uo=0;在负载电流为负的区间,V1和V4导通时,电流通过VD1和VD4,uo=Ud,V4关断,V3开通后,电流从V3和VD1续流,uo=0。
同样,在uo的负半周,V2保持通态,V1保持断态,V3和V4交替通断。
模型:
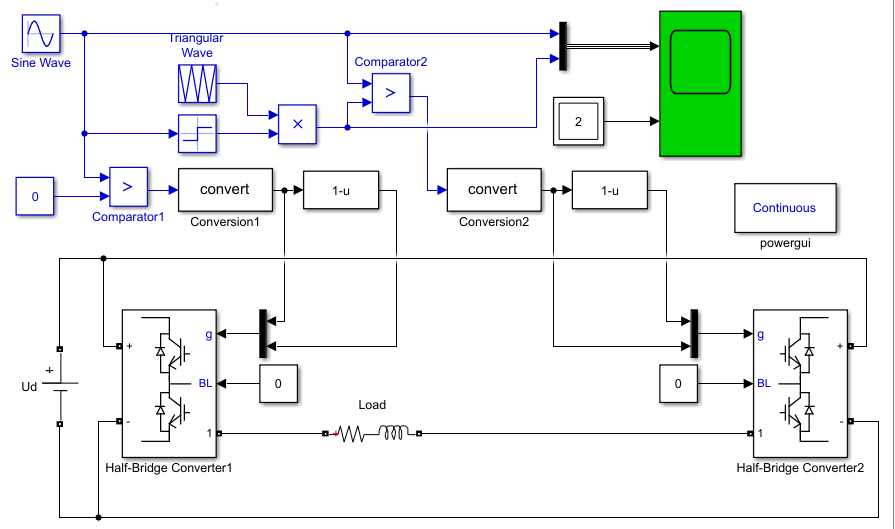
波形:
2. 三相桥式
2.1 调制法
课本P166
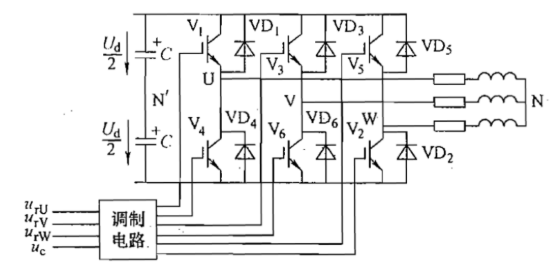
urU、urV、urW三相依次相差120°,每相的控制方式和单相桥式双极性电路相同。
uUN'、uVN'、uWN'的PWM波形都只有±Ud/2两种电平,但是负载相电压有(±2/3)Ud、(±1/3)Ud和0共5中电平。
模型:
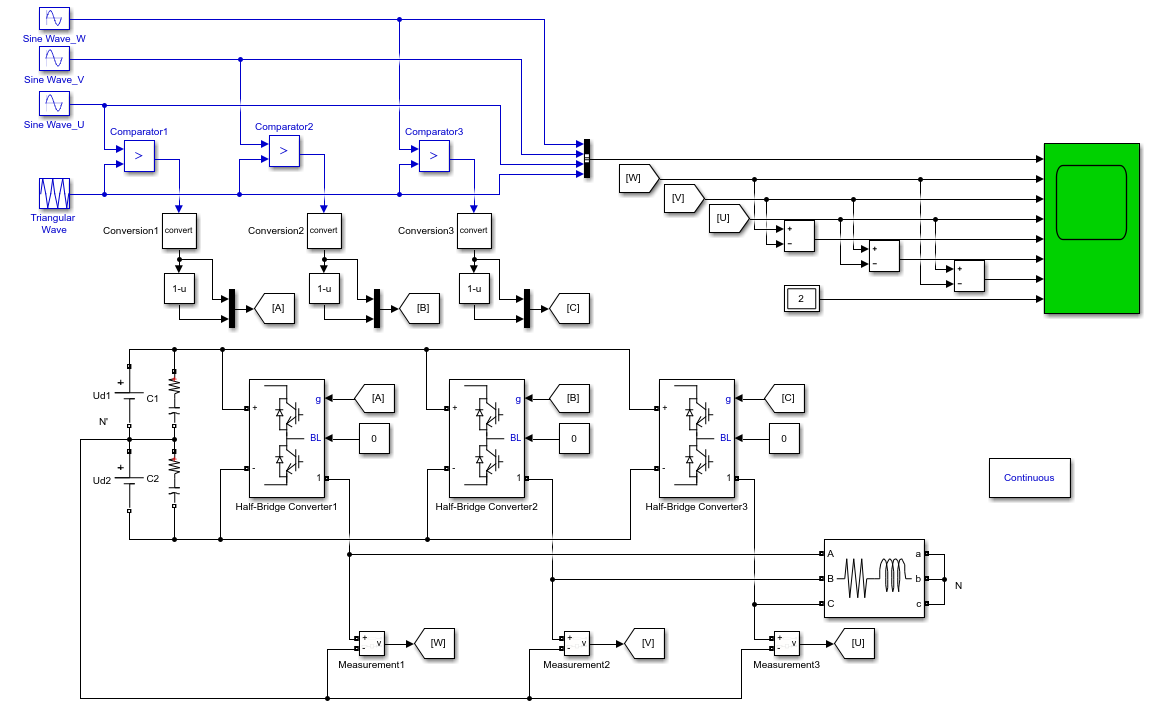
波形:
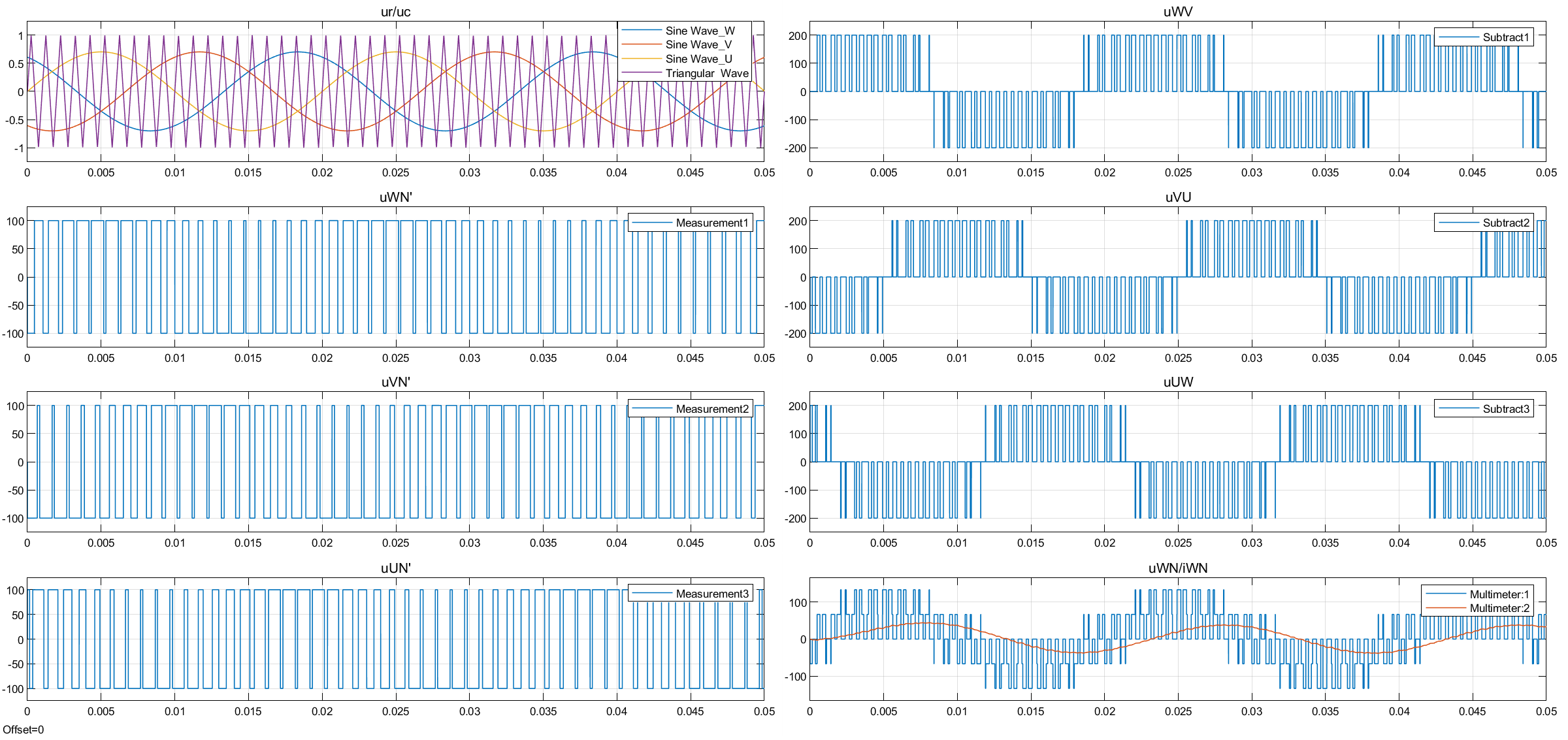
2.2 计算法(特定谐波消去法)

式7-3:1/4周期对称波形
\[u(\omega t) = \sum\limits_{n = 1,3,5, \cdot \cdot \cdot }^\infty {{a_n}\sin n\omega t} \]
\[{a_n} = \frac{4}{\pi }\int_0^{\frac{\pi }{2}} {u(\omega t)\sin } n\omega t{\rm{d\omega t}}\]
式7-4:
\[\begin{array}{l}
{{\rm{a}}_n} = \frac{4}{\pi }\int_0^{\frac{\pi }{2}} {\frac{{{U_d}}}{2}\sin } n\omega t{\rm{d\omega t}} + \frac{4}{\pi }\left( {\int_0^{\frac{\pi }{2}} { - \frac{{{U_d}}}{2}\sin } n\omega t} \right){\rm{d\omega t}}\\
\;\;\;\;\;\;\; + \frac{4}{\pi }\int_0^{\frac{\pi }{2}} {\frac{{{U_d}}}{2}\sin } n\omega t{\rm{d\omega t}} + \frac{4}{\pi }\left( {\int_0^{\frac{\pi }{2}} { - \frac{{{U_d}}}{2}\sin } n\omega t} \right){\rm{d\omega t}}\\
\;\;\;\;\;\;\; = \frac{{2{U_d}}}{{n\pi }}(1 - \cos n{\alpha _1} + 2\cos n{\alpha _2} - 2\cos n{\alpha _3})
\end{array}\]
通常考虑消去5次和7次谐波(式7-5):
\[\left\{ \begin{array}{l}
{a_1} = \frac{{2{U_d}}}{\pi }(1 - \cos {\alpha _1} + 2\cos {\alpha _2} - 2\cos {\alpha _3})\\
{a_5} = \frac{{2{U_d}}}{{5\pi }}(1 - \cos 5{\alpha _1} + 2\cos 5{\alpha _2} - 2\cos 5{\alpha _3}) = 0\\
{a_7} = \frac{{2{U_d}}}{{7\pi }}(1 - \cos 7{\alpha _1} + 2\cos 7{\alpha _2} - 2\cos 7{\alpha _3}) = 0
\end{array} \right.\]
经试验,因上述方程比较复杂,不能得到很好的解,我们转而去利用极值方法寻求其近似解。
构造函数如下:
function F = root(alpha) a1=2*200/pi*(1-2*cos(alpha(1))+2*cos(alpha(2))-2*cos(alpha(3))); a5=2*200/5/pi*(1-2*cos(5*alpha(1))+2*cos(5*alpha(2))-2*cos(5*alpha(3))); a7=2*200/7/pi*(1-2*cos(7*alpha(1))+2*cos(7*alpha(2))-2*cos(7*alpha(3))); F=(a1-30)^2+a5^2+a7^2; end
通过求解F的最小值,可以得到${a_1} = 30$,${a_5} = 0$,${a_7} = 0$的近似解。
这里我们通过fminunc函数求极值,并在$0$~$\frac{\pi }{2}$范围内随机确定初始值,进行1000次试验,找到其中满足条件的最小值。条件指的是${\alpha _1}$、${\alpha _2}$、${\alpha _3}$在$0$~$\frac{\pi }{2}$范围内顺序排列。
min=100;
for i=1:1000
[alpha,fval] = fminunc(@root,rand(1,3)*pi/2);
if(0<alpha(1)&&alpha(1)<alpha(2)&&alpha(2)<alpha(3)&&alpha(3)<pi/2)
if fval<min
min=fval;
alpha0=alpha;
end
end
end
alpha=alpha0
得到一组alpha值如下:

最小值如下:
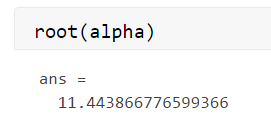
可以看到,最小值与0之间仍有一定差距。
根据${\alpha _1}$、${\alpha _2}$、${\alpha _3}$在$0$~$2\pi $范围内扩展转折点,得到向量t和u。
f=50; t1=[0,alpha,pi-fliplr(alpha)]; t2=pi+t1; t=[t1,t2,2*pi]./(2*pi)./f; u=[repmat([1,0],[1,7]),1]; stairs(t,u);ylim([-0.2,1.2]);
图像如下:
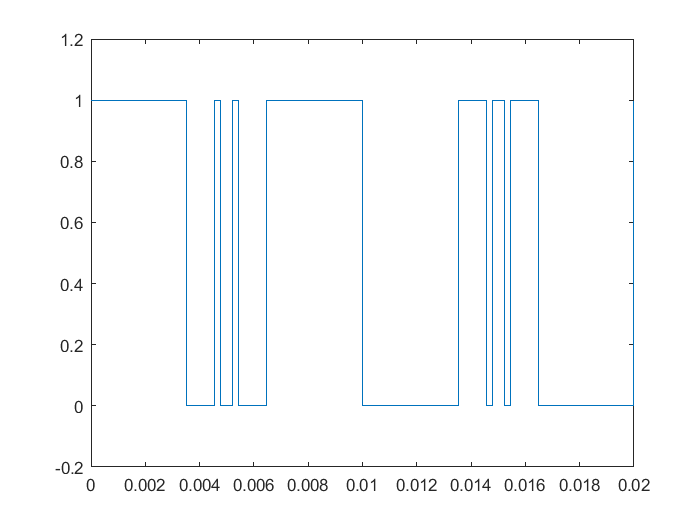
利用t和u以1e-6的间隔构造时间向量和控制向量,存入文件。
t0=0:1e-6:0.08;
u0=zeros(size(t0));
for i=1:length(t0)
for j=1:(length(t)-1)
if mod(t0(i),1/f)>t(j) && mod(t0(i),1/f)<t(j+1)
u0(i)=u(j);
break
end
end
end
matrix=[t0;u0];
save matrix.mat matrix
模型:
驱动信号部分如下图,其余部分和调制法相同。

对uUN‘进行谐波分析,结果如下:
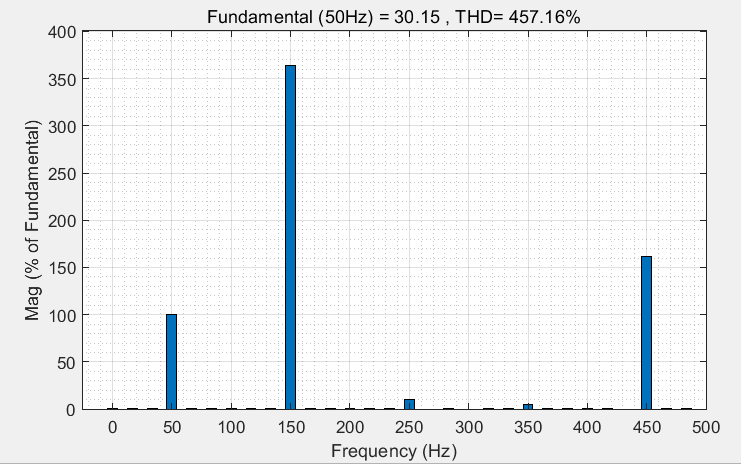
可以看到,基波幅值为30.15,接近预期值30。5次和7次谐波分量较小,3次谐波很大。
列表结果如下:

示波器波形:

对输出电流进行谐波分析:
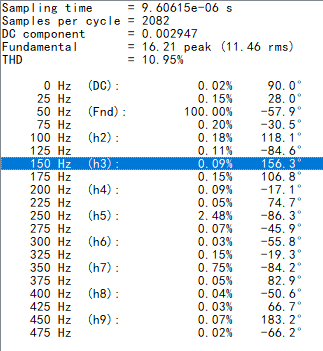
可以看到,在输出电流中,相电压所含的3次谐波已经相互抵消。
3. PWM跟踪(滞环比较)
课本P177
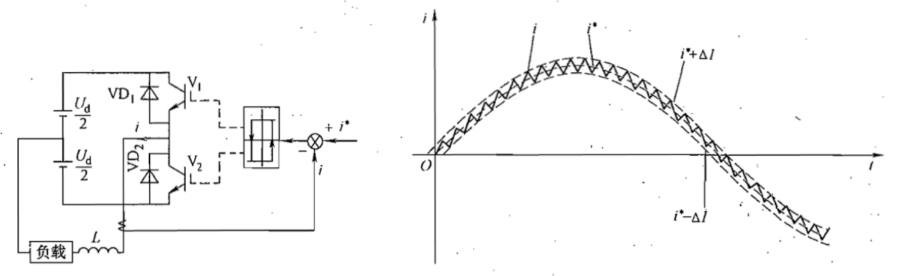
把指定电流i*和实际输出电流i的偏差i*-i作为带有滞环特性的比较器的输入,通过其输出来控制功率器件V1和V2的通断。
环宽过宽时,开关动作频率低,跟踪误差大;环宽过窄时,跟踪误差小,但开关频率过高,开关损耗随之增大。
模型:

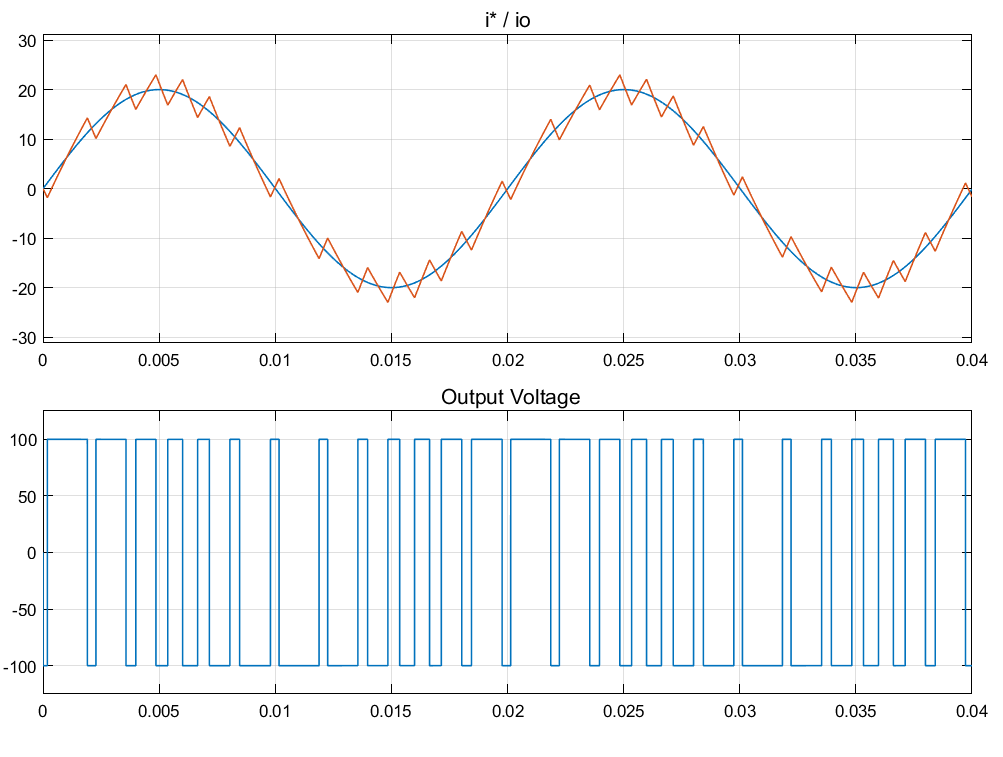
环宽设置为3,得到波形如下:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号