电力电子Simulink仿真——直流直流
1. 基本斩波电路
1.1 降压斩波
课本P120
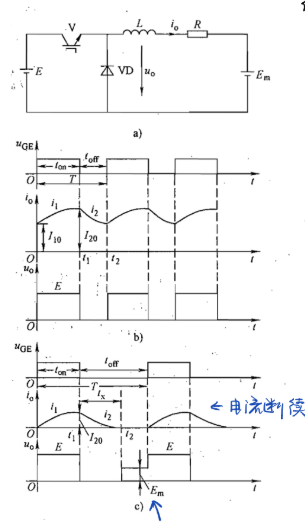
V导通,电源E向负载供电,负载电压u0=E,负载电流按指数规律上升。
V关断,负载电流经二极管VD续流,负载电压近似为零,负载电流呈指数曲线下降。
为使负载电流连续且脉动小,通常串联的电感L值较大。
式5-1
\[{U_0} = \frac{{{t_{on}}}}{T}E = \alpha E\]
模型:

- 输入电压:200V;
- 触发占空比:70%;
- 开关频率:1000Hz;
- 负载:5Ω,0.01H,80V反电势;
- 输出电压均值:138.8。(计算值200×70%=140)
波形:
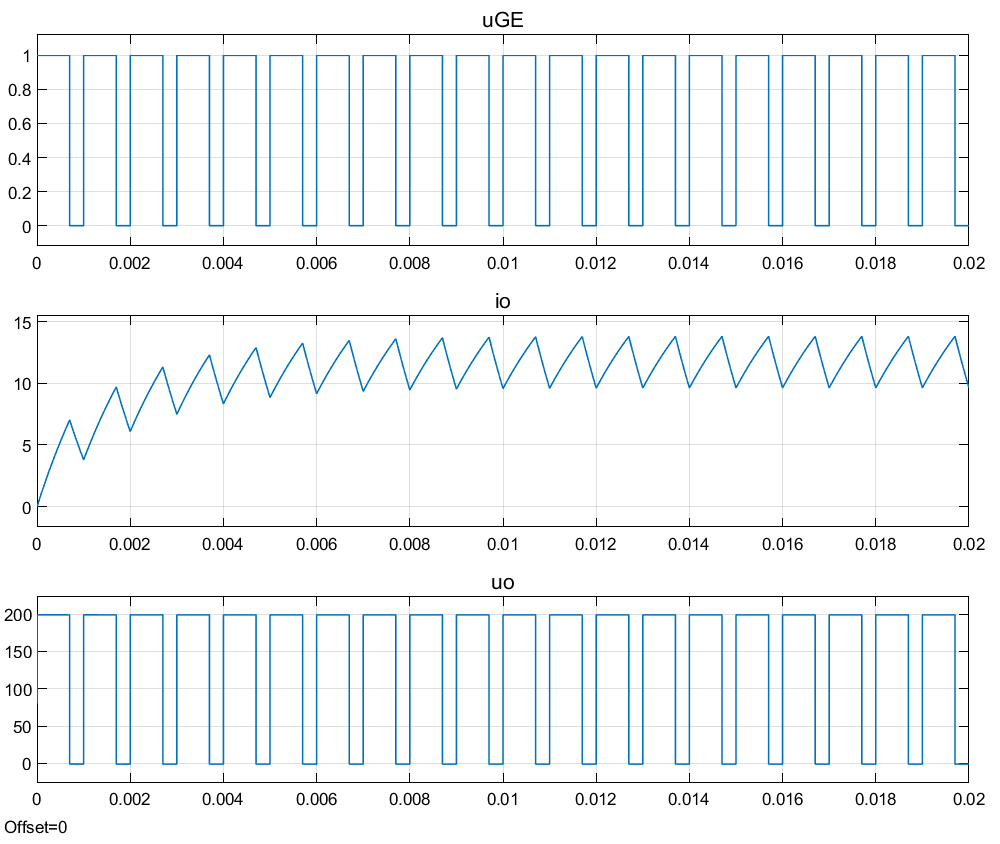
输出电流:

式5-9、5-10:
\[{I_{10}} = \left( {\frac{{{e^{\alpha \rho }} - 1}}{{{e^\rho } - 1}} - m} \right)\frac{E}{R}\]
\[{I_{20}} = \left( {\frac{{1 - {e^{ - \alpha \rho }}}}{{1 - {e^{ - \rho }}}} - m} \right)\frac{E}{R}\]
这里:
\[\alpha = 0.7\]
\[m = \frac{{{E_m}}}{E} = 0.4\]
\[\tau = \frac{L}{R} = 0.002\]
\[T = 0.001\]
\[\rho = \frac{T}{\tau } = 0.5\]
| 计算值 | 测量值 | |
| 电流最大值 | 14.02 | 13.85 |
| 电流最小值 | 9.84 | 9.55 |
1.2 升压斩波
课本P123
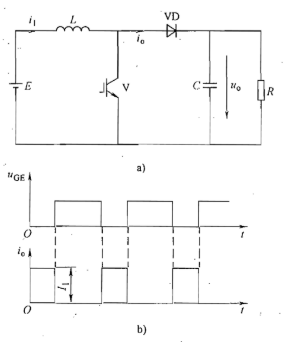
V处于通态时,电源E向电感L充电,充电电流基本恒定,同时电容C向负载放电。
当V处于断态时E和L共同向电容C充电同时向负载提供能量。
式5-21:
\[{U_0} = \frac{T}{{{t_{off}}}}E = \frac{1}{\beta }E\]
其中,$\beta = 1 - \alpha $。
模型:

- 输入电压:100V;
- 触发占空比:50%;
- 开关频率:10000Hz;
- 电感:1e-3H;
- 电容:2e-5F;
- 电阻:50Ω;
- 输出电压均值:197.6V。(计算值100/0.5=200V)
波形:

1.3 升降压斩波
课本P127

V通态,电源E经V向电感L供电,使其储存能量,同时电容C向负载供电。
V断态,电感L中的能量向负载释放,负载电压极性为上负下正。
模型:
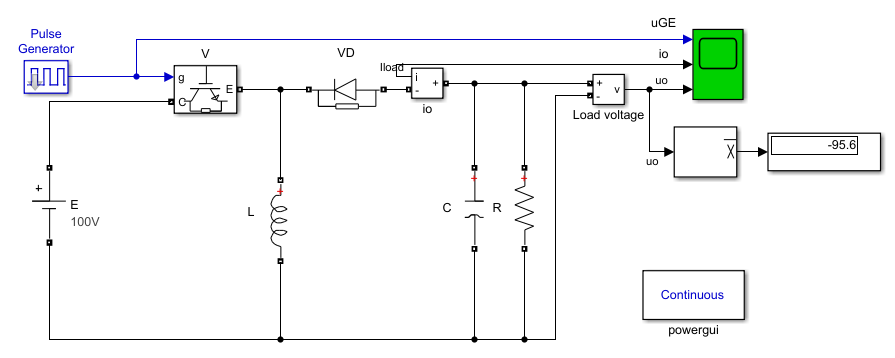
- 电源电压:100V;
- 触发占空比:50%;
- 开关频率:1000Hz;
- 电感:5e-03;
- 电容:1e-3F;
- 电阻:5Ω。
波形:
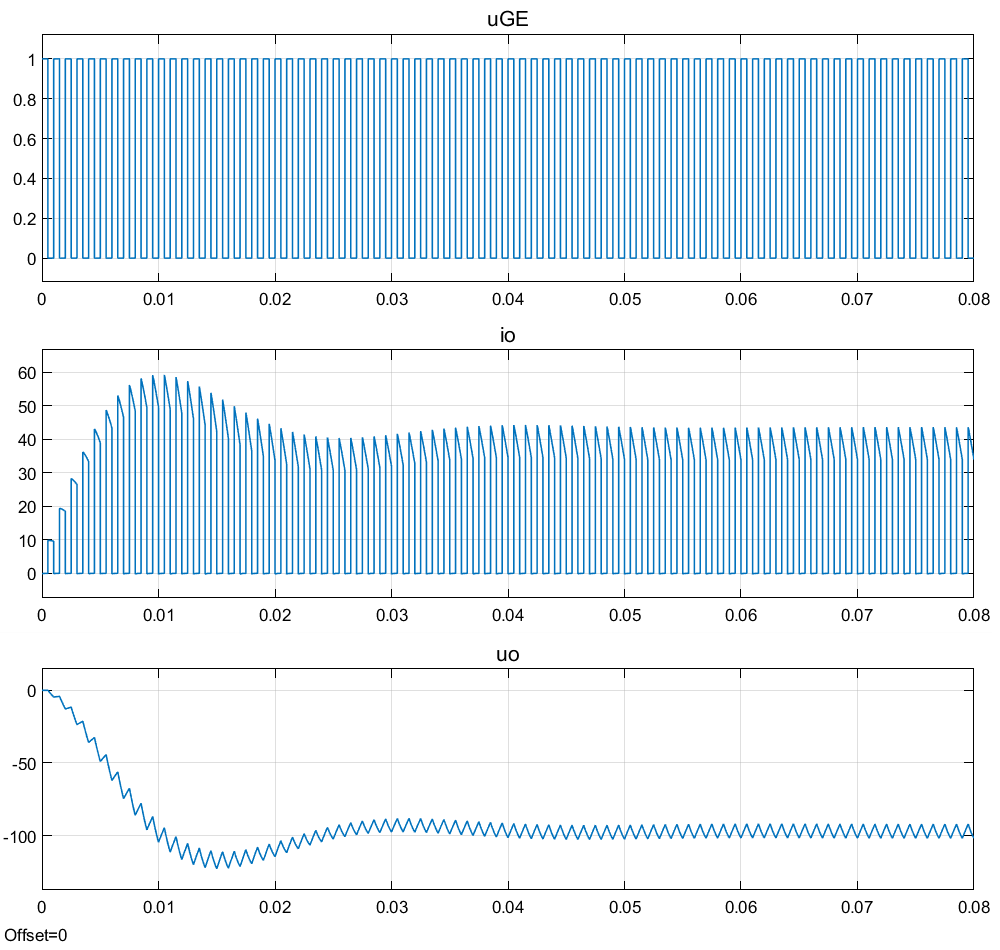
| u0计算值 | u0测量值 | |
| $\alpha = {25^ \circ }$ | -33.3 | -31.99 |
| $\alpha = {50^ \circ }$ | -100 | -97.17 |
| $\alpha = {75^ \circ }$ | -300 | -286.5 |
1.4 电流可逆斩波电路
课本P129

V1和VD1构成降压斩波电路,用电源向直流电动机供电,电动机电动运行,工作于第1象限;V2和VD1构成升压斩波电路,把直流电动机的动能转变为电能反馈到电源,是电动机作再生制动运行,工作于第2象限。
模型:
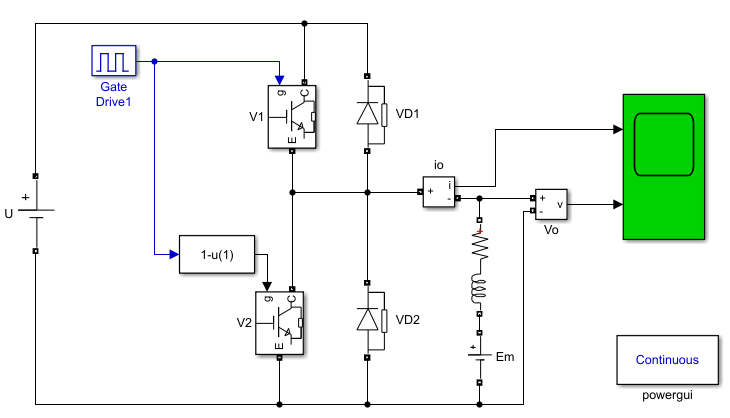
波形:

2. 多相多重斩波电路
课本P131

三相三重斩波电路相当于由三个降压斩波电路并联而成,V1、V2、V3依次导通,相位相差1/3周期,波形相同,总输出电流为三个斩波电路单元输出电路之和,其平均值为单元输出电路平均值的三倍,脉动频率也为三倍,但是总输出电流的脉动幅值变得很小。
模型:
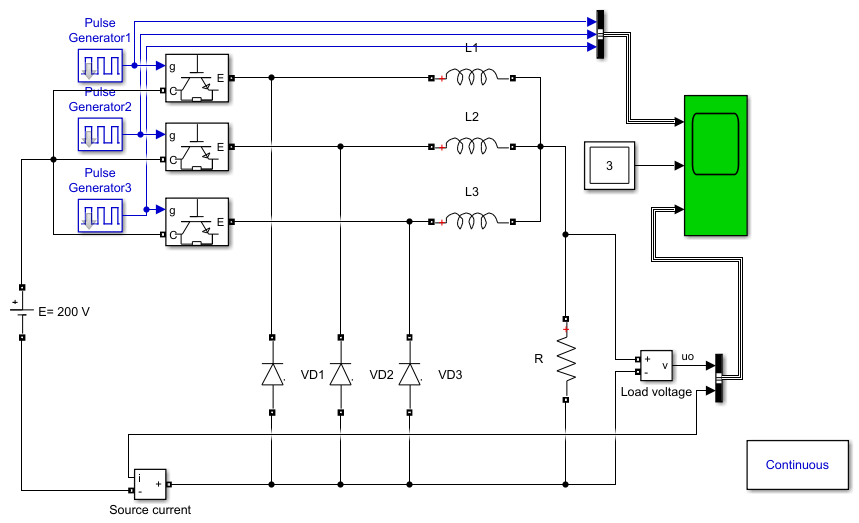
波形:
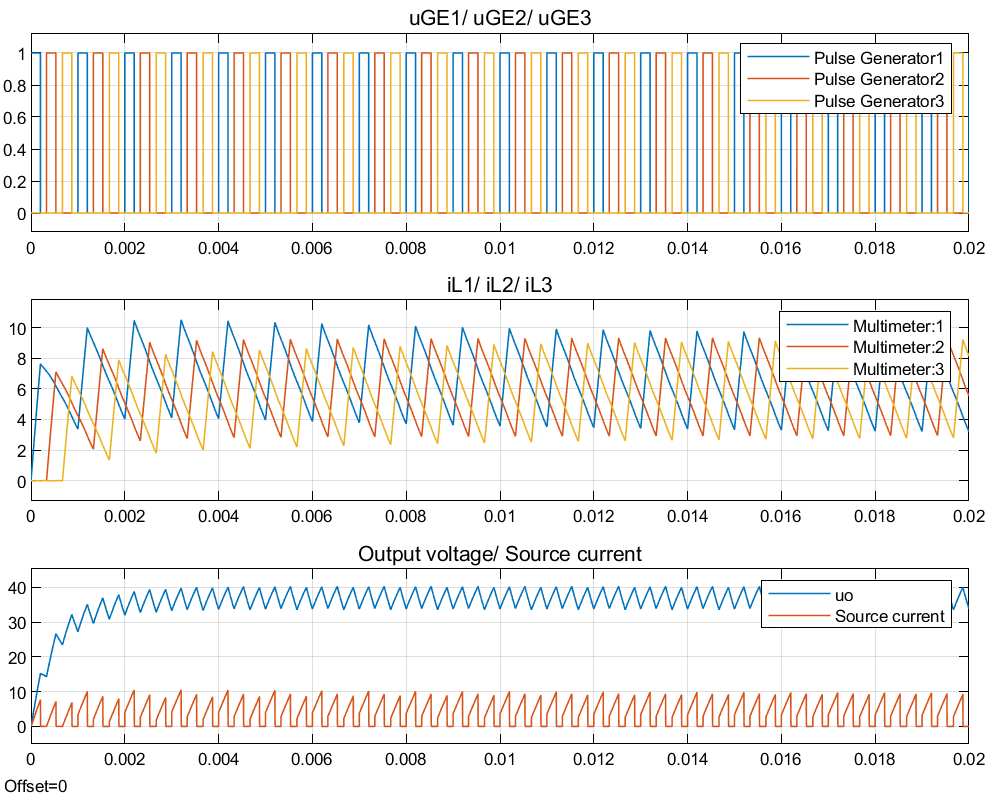
谐波分析:
单个单元
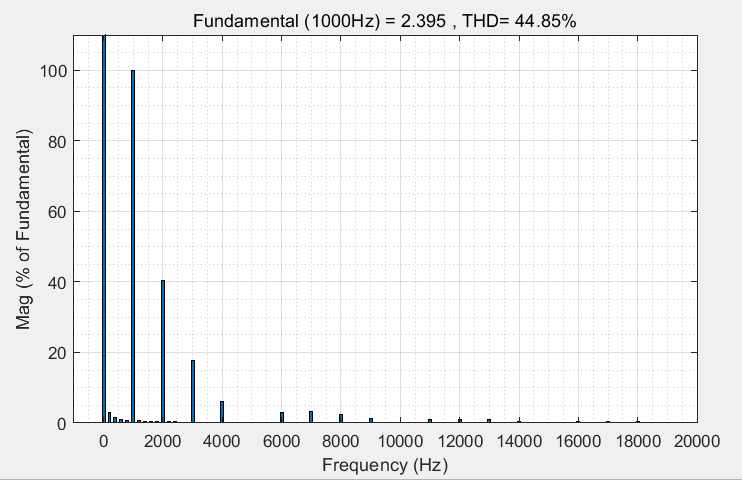
总电流

总电流谐波含量明显较低。
3. 带隔离的直流直流
3.1 正激
课本P132


开关S开通后,变压器绕组W1两端的电压为上正下负,与其耦合的绕组W2两端的电压也是上正下负;因此VD1处于通态,VD2断态,电感L的电流逐渐增长。
S关断后,电感L通过VD2续流,VD1关断,L的电流逐渐下降。S关断后变压器的励磁电流经绕组W3和VD3流回电源。所以S关断后承受的电压为${u_S} = \left( {1 + \frac{{{N_1}}}{{{N_3}}}} \right){U_i}$。
式5-52:
\[\frac{{{U_o}}}{{{U_i}}} = \alpha \frac{{{N_2}}}{{{N_1}}}\]
模型:
- N1:N2:N3=1:1:1;
- 输入电压:100V;
- 占空比:40%;
- 开关频率:20000Hz;
- 电感:0.001H;
- 电容:5e-5F;
- 负载:5Ω;
- 输出电压:39.54V(理论值40V)。

输出波形:
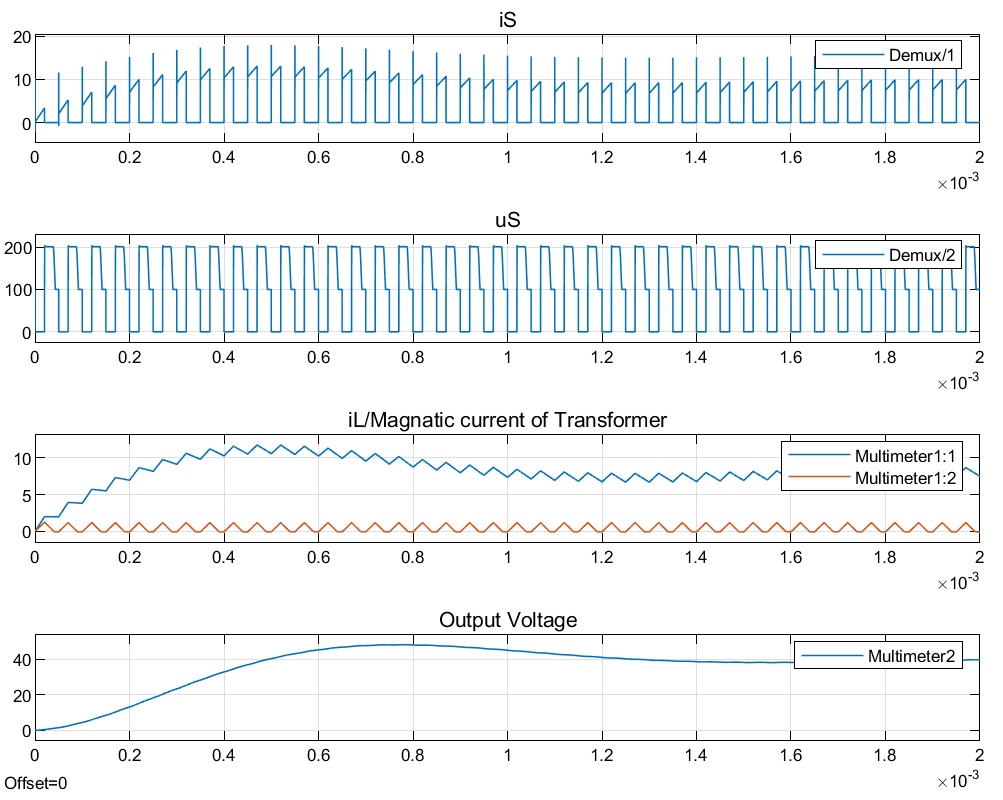
3.2 反激
课本P133
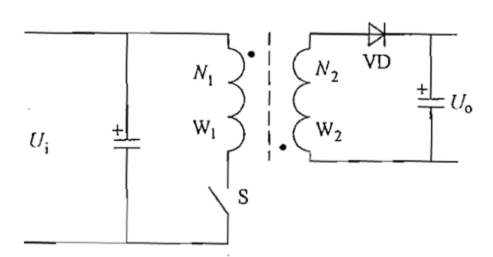
同正激电路不同,反激电路中的变压器起着储能元件的作用,可以看做是一对相互耦合的电感。
S开通后,VD处于断态,绕组W1中的电流线性增长,电感储能增加。
S关断后,绕组W1的电流被切断,变压器中的磁场能量通过绕组W2和VD向输出端释放。S关断后${u_S} = {U_i} + \frac{{{N_1}}}{{{N_2}}}{U_o}$。
式5-53:
\[\frac{{{U_o}}}{{{U_i}}} = \frac{\alpha }{{1 - \alpha }}\frac{{{N_2}}}{{{N_1}}}\]
模型:
占空比40%,输入100V,输出63.82V(理论值66.66V)。
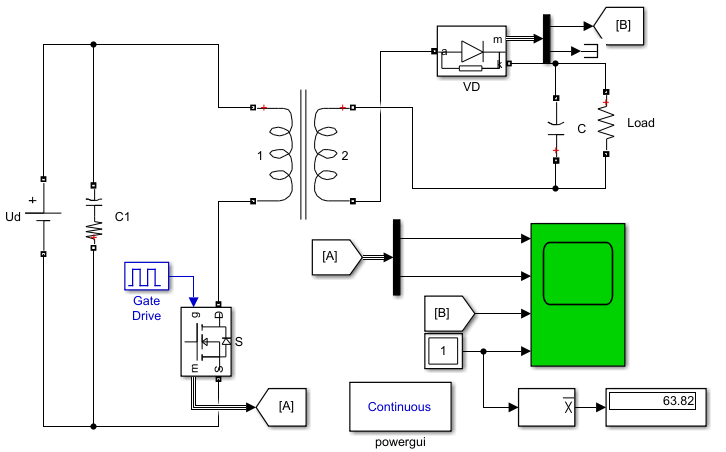
波形:
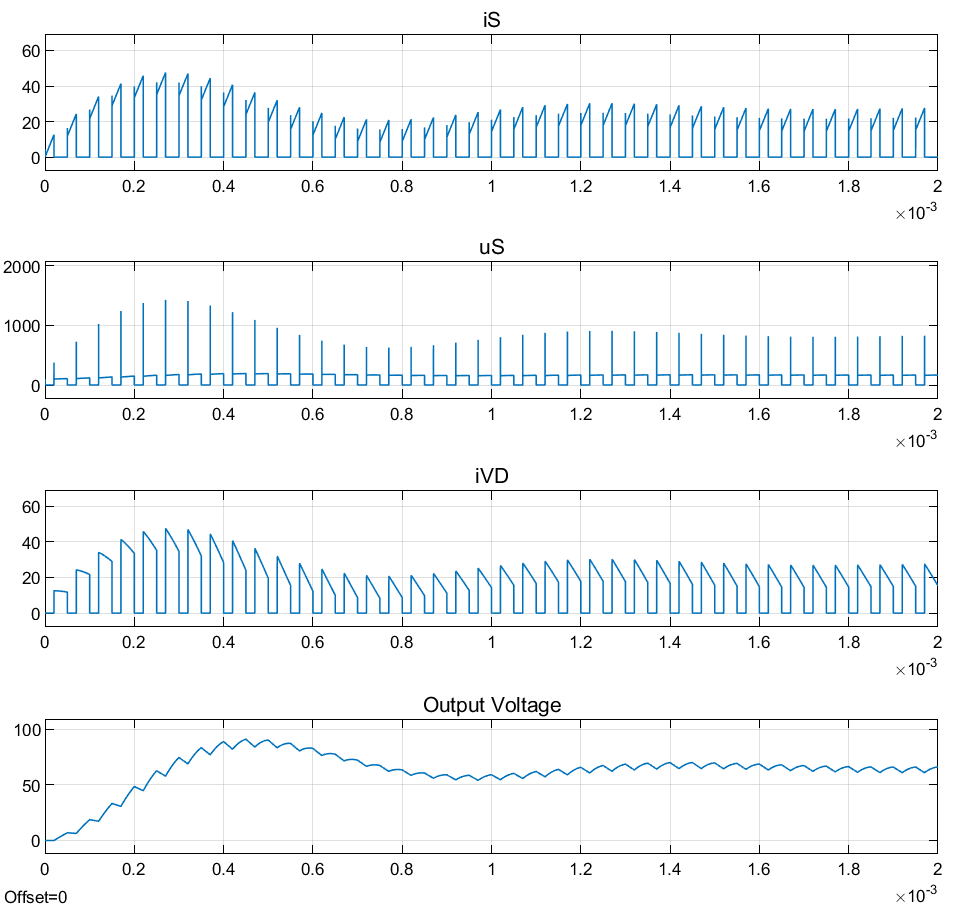
3.3 半桥
课本P134
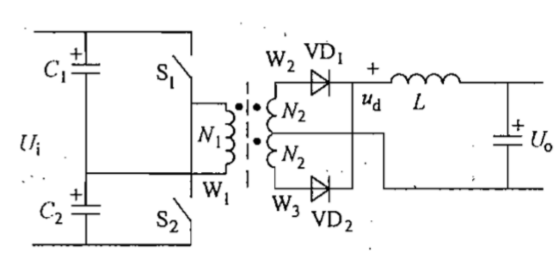
在半桥电路中,变压器一次侧的两端分别连接在电容C1和C2的中点和开关S1和S2的中点。电容C1和C2的中点电压为Ui/2。S1和S2的交替导通,是变压器一次侧形成幅值为Ui/2的交流电压。
改变开关的占空比,就可以改变二次侧整流电压ud的平均值,也就改变了输出电压Uo。
S1导通时,二极管VD1处于通态,S2导通时,二极管VD2处于通态,当两个开关都关断时,变压器绕组W1中的电流为零,根据变压器的磁动势平衡方程,绕组W2和W3中的电流大小相等、方向相反,所以VD1和VD2都处于通态,各分担一半的电流。
S1或S2导通时电感电流逐渐上升,两个开关都关断时,电感L的电流逐渐下降。
式5-54:\[\frac{{{U_o}}}{{{U_i}}} = \alpha \frac{{{N_2}}}{{{N_1}}}\]
模型:
- 输入:100V×2个;
- 占空比:50%;
- 输出电压:29.41V(理论值30V)。
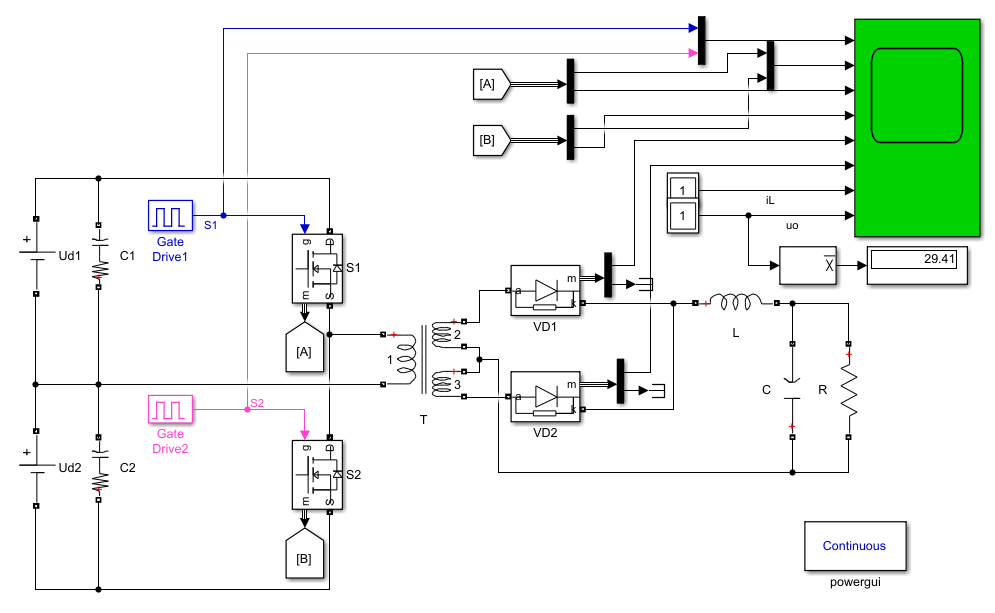
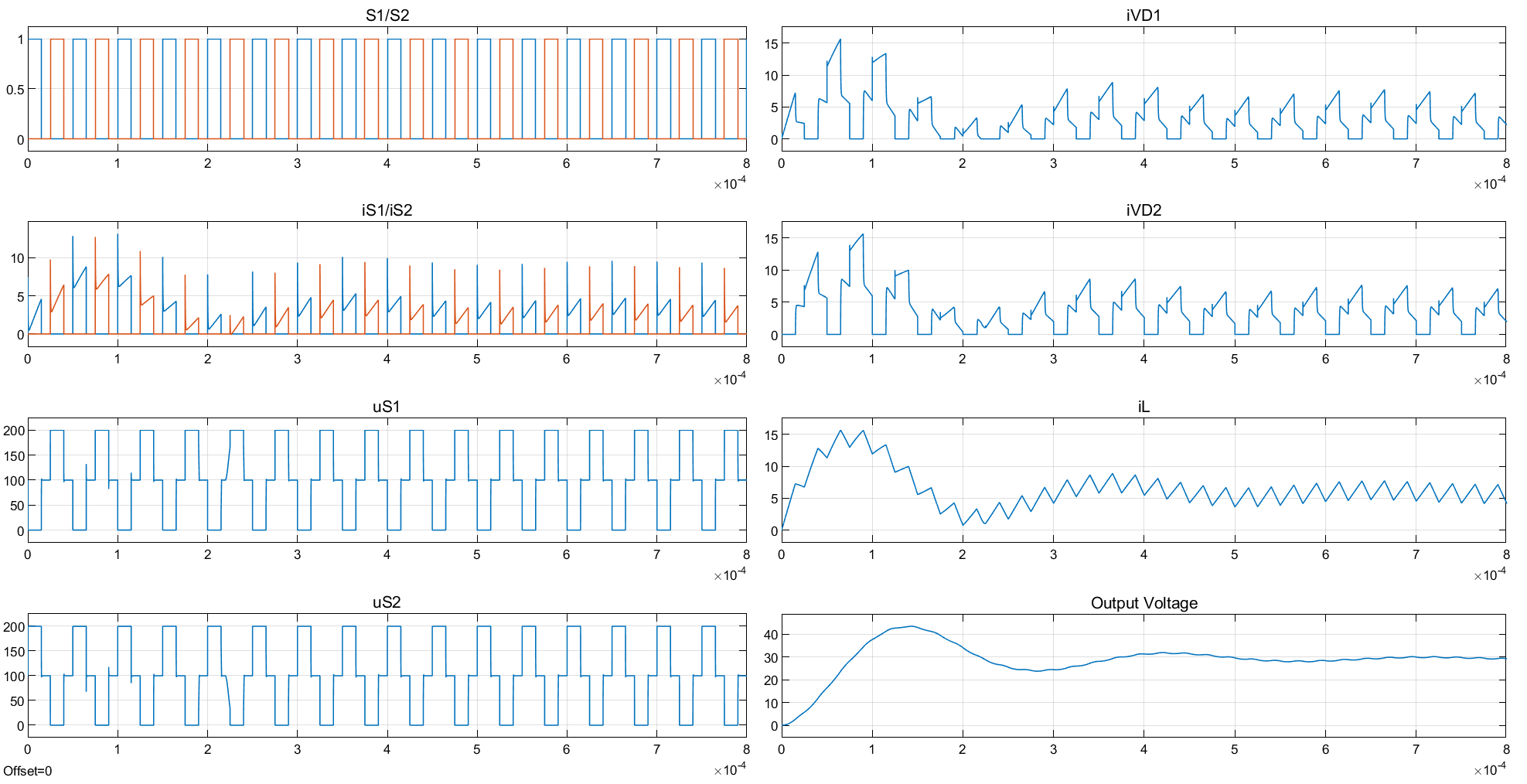
3.4 全桥
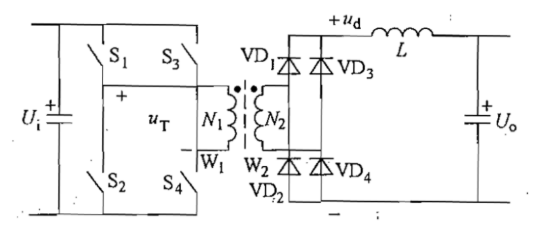
全桥电路中的逆变电路由四个开关组成,互为对角的两个开关交替导通,而同一侧半桥上下的两个开关交替导通,将直流电压逆变成幅值为Ui的交流电压,加载变压器一次侧。
改变开关的占空比,就可以改变整流电压ud的平均值,也就改变了输出电压Uo。
S1与S4开通后,二极管VD1和VD4处于通态,电感电流逐渐上升;S2和S3开通后,二极管VD2和VD3处于通态,电感电流也上升。
当四个开关都关断时,四个二极管都处于通态,各分担一半的电感电流,电感L的电流逐渐下降。
式5-55:\[\frac{{{U_o}}}{{{U_i}}} = 2\alpha \frac{{{N_2}}}{{{N_1}}}\]
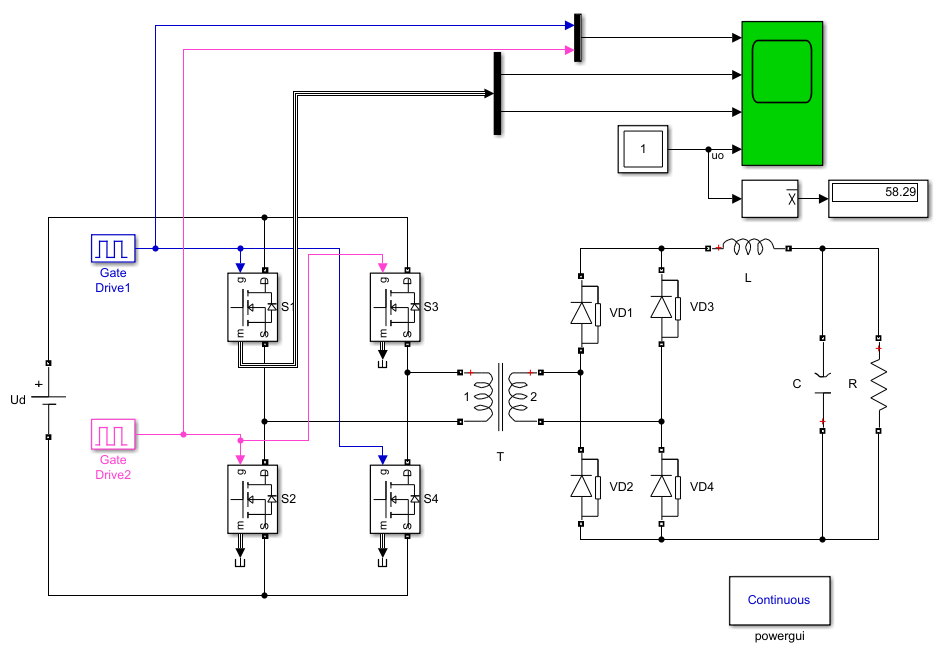
模型:
- 输入电压:200V;
- 变压比:2:1;
- 占空比30%;
- 输出电压58.29V(理论值60V)。
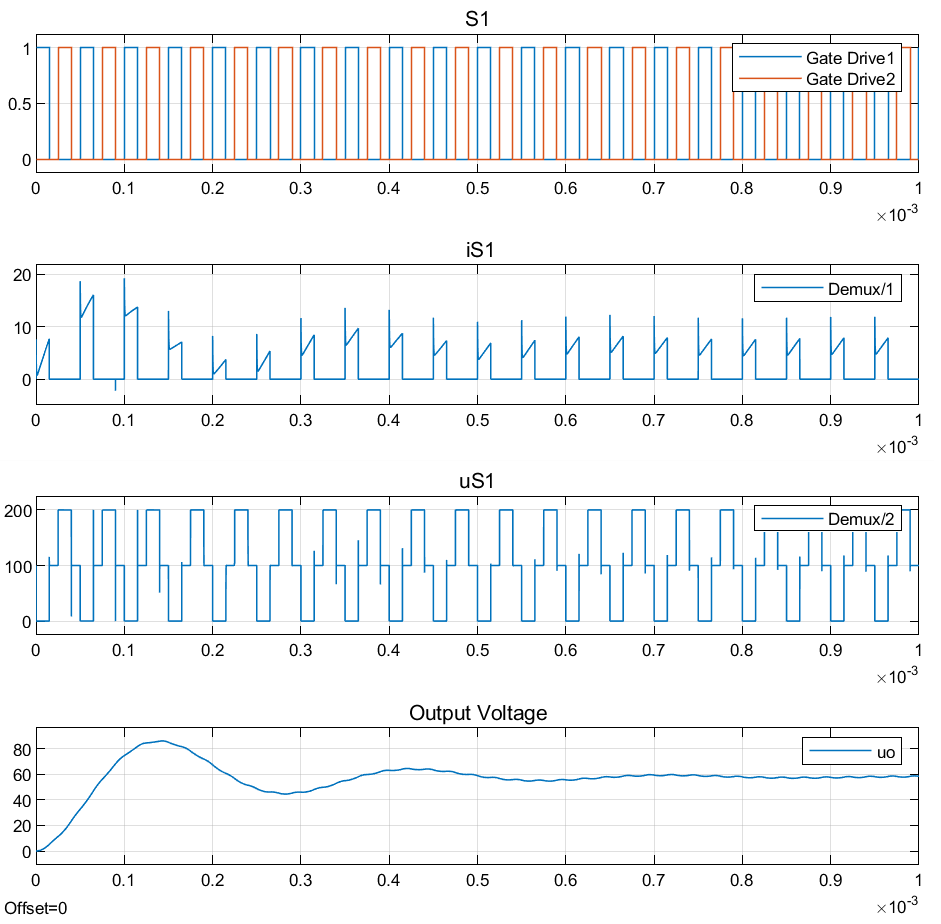
波形:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号