HDU 1542 - Atlantis - [线段树+扫描线]
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1542
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
The input file is terminated by a line containing a single 0. Don’t process it.
Output a blank line after each test case.
题意:
给出n个矩形的左下角和右上角坐标,保证矩形面积大于零,要求n个矩形所覆盖的整个图形的面积。
题解:
属于线段树配合扫描线的模板题,
转载自https://blog.csdn.net/konghhhhh/article/details/78236036的线段树+扫描线基本原理:
假想有一条扫描线,从左往右(从右往左),或者从下往上(从上往下)扫描过整个多边形(或者说畸形……多个矩形叠加后的那个图形)。
如果是竖直方向上扫描,则是离散化横坐标,如果是水平方向上扫描,则是离散化纵坐标。下面的分析都是离散化横坐标的,并且从下往上扫描的。
扫描之前还需要做一个工作,就是保存好所有矩形的上下边,并且按照它们所处的高度进行排序,另外如果是上边我们给他一个值$-1$,下边给他一个值$1$,我们用一个结构体来保存所有的上下边:
struct Segment { double l,r,h; //l和r表示这条上下边的左右坐标,h是这条边所处的高度 int f; //所赋的值,1或-1 }
接着扫描线从下往上扫描,每遇到一条上下边就停下来,将这条线段投影到总区间上(总区间就是整个多边形横跨的长度),这个投影对应的其实是个插入和删除线段操作。
还记得给他们赋的值$1$或$-1$吗,下边是$1$,扫描到下边的话相当于往总区间插入一条线段,上边是$-1$,扫描到上边相当于在总区间删除一条线段(如果说插入删除比较抽象,那么就直白说,扫描到下边,投影到总区间,对应的那一段的值都要增$1$,扫描到上边对应的那一段的值都要减$1$,如果总区间某一段的值为$0$,说明其实没有线段覆盖到它,为正数则有,那会不会为负数呢?是不可能的,可以自己思考一下)。
每扫描到一条上下边后并投影到总区间后,就判断总区间现在被覆盖的总长度,然后用下一条边的高度减去当前这条边的高度,乘上总区间被覆盖的长度,就能得到一块面积,并依此做下去,就能得到最后的面积。
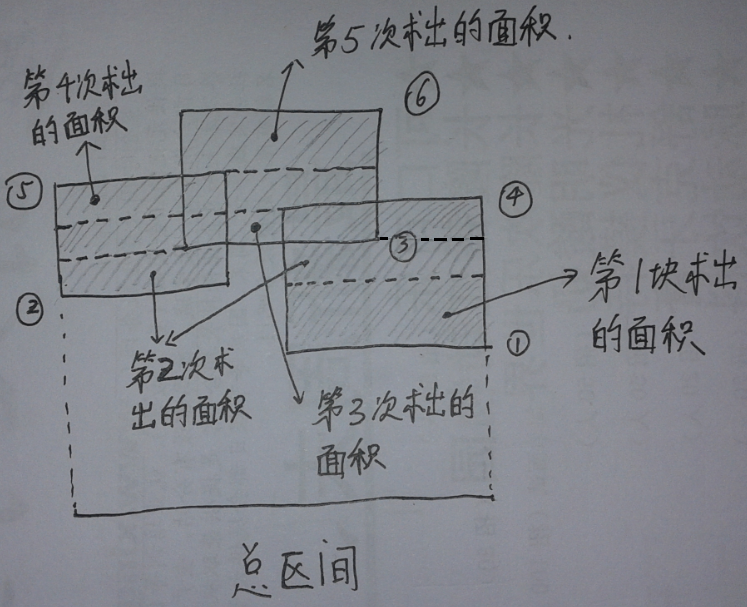
当然了,我们知道,线段树维护的是点,而这里我们要维护的是连续的区间,
因此我们给每个点赋予新的意义:对于第 i 个点,其代表区间 [ i , i+1 ),
然后,本题对横轴坐标进行去重离散化,假设最后剩下size个横坐标,存储在数组 x[1~size]中,那么我们线段树就从 点0 到 点size-1 建树,这样就能维护整个总区间,
同时我们也需要对线段树进行一定的修改,体现在代码中。
AC代码:
#include<bits/stdc++.h> typedef long long ll; using namespace std; const int maxn=210; int n; vector<double> x; inline int getID(double val){return lower_bound(x.begin(),x.end(),val)-x.begin();} struct Segment { double l,r; double h; int flag; }segment[maxn]; bool cmp(Segment a,Segment b){return a.h<b.h;} /********************************* Segment Tree - st *********************************/ struct Node{ int l,r; int s; double len; }node[4*maxn]; void pushup(int rt) { if(node[rt].s) node[rt].len=x[(node[rt].r+1)]-x[(node[rt].l)]; else if(node[rt].l==node[rt].r) node[rt].len=0; else node[rt].len=node[rt*2].len+node[rt*2+1].len; } void build(int rt,int l,int r) { if(l>r) return; node[rt].l=l; node[rt].r=r; node[rt].s=0; node[rt].len=0; if(l==r) return; else { int mid=l+(r-l)/2; build(rt*2,l,mid); build(rt*2+1,mid+1,r); pushup(rt); } } void update(int root,int st,int ed,int val) { if(st>node[root].r || ed<node[root].l) return; if(st<=node[root].l && node[root].r<=ed) { node[root].s+=val; pushup(root); } else { update(root*2,st,ed,val); update(root*2+1,st,ed,val); pushup(root); } } /********************************* Segment Tree - st *********************************/ int main() { int kase=0; while(scanf("%d",&n) && n!=0) { x.clear(); for(int i=1;i<=n;i++) { double x1,x2,y1,y2; scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); Segment &s1=segment[2*i-1]; Segment &s2=segment[2*i]; s1.l=s2.l=x1; s1.r=s2.r=x2; s1.h=y1; s2.h=y2; s1.flag=1; s2.flag=-1; x.push_back(x1); x.push_back(x2); } sort(segment+1,segment+2*n+1,cmp); //横坐标去重离散化 sort(x.begin(),x.end()); x.erase(unique(x.begin(),x.end()),x.end()); build(1,0,x.size()); double ans=0; for(int i=1;i<=2*n;i++) { int l=getID(segment[i].l); int r=getID(segment[i].r); update(1,l,r-1,segment[i].flag); ans+=node[1].len*(segment[i+1].h-segment[i].h); } printf("Test case #%d\n",++kase); printf("Total explored area: %.2f\n\n",ans); } }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号