伸展树(Splay Tree)进阶 - 从原理到实现
目录
1 简介
伸展树(Splay Tree),是一种二叉搜索树(Binary Search Tree,又称二叉排序树Binary Sort Tree),由丹尼尔·斯立特(Daniel Sleator)和 罗伯特·恩卓·塔扬(Robert Endre Tarjan)在1985年发明。
平衡的二叉搜索树一般分为两类:
严格维护平衡的,树的高度控制在$\log _2 n$,使得每次操作都能使得时间复杂度控制在$O\left( {\log n} \right)$,例如AVL树,红黑树;
非严格维护平衡的,不能保证每次操作都控制在$O\left( {\log n} \right)$,但是每次操作均摊时间复杂度为$O\left( {\log n} \right)$,例如伸展树。
伸展树的优点在于无需记录额外的值来维护树的信息,同时支持的操作很多;
伸展树的缺点主要在于速度慢,最坏情况可能使得树退化成一条链;
2 基础操作
2.1 旋转
旋转操作,它可以使得某一个结点提升到他父亲的位置而不破坏平衡二叉树的性质。
如下图,很好地展现了ZIG旋转和ZAG旋转的具体操作:

图2.1 ZIG旋转和ZAG旋转
在图2.1中,$x$ 和 $y$ 分别代表两个节点,$A,B,C$ 分别代表三棵子树,
显然它们满足性质:对于任意一个节点,它大于等于其左子树中的任何一个节点,并且小于等于其右子树中的任何一个节点。
那么,易知ZIG旋转和ZAG旋转不会破坏上述性质;
不妨称 ZIG($x$) 为将 $x$ 节点右旋,ZAG($y$) 为将 $y$ 节点左旋。
具体如何实现ZIG操作和ZAG操作,很简单:
ZIG操作:
ZIG($x$):将 $x$ 节点的右子树 $B$ 拿开,将 $y$ 节点变为 $x$ 节点的右儿子,再把子树 $B$ 变为 $y$ 节点的左子树。
ZAG操作:
ZIG($y$):将 $y$ 节点的左子树 $B$ 拿开,将 $x$ 节点变为 $y$ 节点的左儿子,再把子树 $B$ 变为 $x$ 节点的右子树。
事实上,不难发现ZIG操作和ZAG操作很相似,而实际实现中我们通常可以使用一个函数来实现他们的功能。
2.2 伸展操作
伸展树之所以叫做伸展树,伸展树之所以能够达到每次操作均摊时间复杂度为$O\left( {\log n} \right)$,其关键都在于伸展操作。
而伸展操作的目的,就是把当前节点,移动至树根,或者说,把当前节点变成根节点。
若 $x,y$ 两个节点中,$y$ 节点是 $x$ 节点的父亲节点,且 $y$ 节点是根节点,那么基础的ZIG操作或者ZAG操作就可以使得 $x$ 节点变为根节点。
但是要是 $y$ 节点不是根节点呢?
那么,不妨假设有三个节点 $x,y,z$,它们的关系:$y$ 节点是 $x$ 节点的父亲节点,$z$ 节点是 $y$ 节点的父亲节点。
那么这三个节点有如下四种情况:
① ZIG-ZIG操作
$x$ 节点是 $y$ 节点的左儿子,$y$ 节点是 $z$ 节点的左儿子:
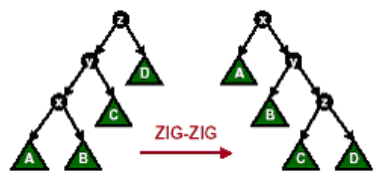
图2.2 ZIG-ZIG操作
显然,这是两次ZIG操作的组合,我们先ZIG($y$)再ZIG($x$)即可。
② ZAG-ZAG操作
$x$ 节点是 $y$ 节点的右儿子,$y$ 节点是 $z$ 节点的右儿子,
显然,这是两次ZAG操作的组合,我们先ZAG($y$)再ZAG($x$)即可。
③ ZIG-ZAG操作
$x$ 节点是 $y$ 节点的左儿子,$y$ 节点是 $z$ 节点的右儿子:

图2.3 ZIG-ZAG操作
显然,我们先ZIG($x$)再ZAG($x$)即可。
④ ZAG-ZIG操作
$x$ 节点是 $y$ 节点的右儿子,$y$ 节点是 $z$ 节点的左儿子,
显然,我们先ZAG($x$)再ZIG($x$)即可。
这四种组合操作,加上基础的ZIG操作和ZAG操作,构成了伸展操作。
3 常规操作
3.1 插入操作
插入操作很简单,对于要插入的元素 $x$,首先从根节点开始,比较 $x$与当前节点的元素的大小,
如果 $x$ 更小,显然要插入到左子树,否则就要插入到右子树中,
如果左(右)子树不为空,那么把左(右)子树的根节点和 $x$ 继续比较,重复上述操作,
如果左(右)子树为空,那么中止循环,并在此位置插入结点,
最后,很重要的,把插入的这个节点伸展成根节点。
3.2 删除操作
对于要删除的节点 $x$,先将其伸展到树根,
求其前驱和后继,我们知道根节点的前驱后继很好求,分别是其左子树中的最靠右的节点和其右子树中最靠左的节点,假设其前驱节点为 $y$,其后继节点为 $z$,
接下来,把节点 $y$ 伸展成根节点,再把节点 $z$ 伸展成根节点的右儿子,
这样一来,节点 $z$ 的左子树必然只有一个节点 $x$,把它删掉就好了。
可能出现特殊情况:
有前驱无后继:
把节点 $y$ 伸展成根节点,删去节点 $y$ 的右儿子。
有后继无前驱:
把节点 $z$ 伸展成根节点,删去节点 $z$ 的左儿子。
无前驱无后继:
整棵树只有一个节点 $x$,删掉即可。
3.3 查找操作
伸展树作为一种二叉搜索树,怎么二叉搜索应该不用再说了吧……
记得将查找到的节点伸展成根节点即可。
3.4 查找某数的排名、查找某排名的数
3.4.1 查找某数的排名
首先查找该元素,将找到的节点伸展成根节点,则根节点的左子树的节点数加一等于该元素的编号。
3.4.2 查找某排名的数
假设要查询的排名为 $i$,从根节点开始查询,假设左子树的节点数为 $k$:
若 $k + 1 > i$,则在左子树继续查询 $i$;
若 $k + 1 = i$,则返回当前节点的元素;
若 $k + 1 < i$,则在右子树继续查询 $i - k + 1$;
最后记得将查找到的节点伸展成根节点即可。
4 代码实现
#include<bits/stdc++.h> using namespace std; const int maxn=100010; struct Node { Node *par,*ls,*rs; int val; //本节点元素 int size; //统领的树的大小 int cnt; //本节点的元素出现了几次 Node(int val=0,int size=0,int cnt=0) { this->val = val; this->size = size; this->cnt = cnt; } void calc_size() { size = ls->size + rs->size + cnt; } }; struct SplayTree { Node nullnode, *null=&nullnode; Node *root; int size; //统计整棵树的节点个数 Node node[maxn]; void init() { this->root = null; this->size = 0; } void zig(Node *x) { if(x != x->par->ls) return; Node *y = x->par; Node *rt = y->par; y->ls = x->rs; if(x->rs != null) x->rs->par = y; x->par = rt; if(rt != null) { if(y == rt->rs) rt->rs = x; else rt->ls = x; } x->rs = y; y->par = x; x->calc_size(); y->calc_size(); } void zag(Node *y) { if(y != y->par->rs) return; Node *x = y->par; Node *rt = x->par; x->rs = y->ls; if(y->ls != null) y->ls->par = x; y->par = rt; if(rt != null) { if(x == rt->rs) rt->rs = y; else rt->ls = y; } y->ls = x; x->par = y; x->calc_size(); y->calc_size(); } void splay(Node *x, Node *target) //将节点x伸展到target的儿子位置处 { if(x == null) return; Node *y; while(x->par != target) { y = x->par; if(x == y->ls) { if(y->par != target && y == y->par->ls) zig(y); zig(x); } else { if(y->par != target && y == y->par->rs) zag(y); zag(x); } } if(target == null) root = x; } Node* ins(int val) //插入一个值 { if(root == null) { size = 0; root = &node[++size]; root->ls = root->rs = root->par = null; root->val = val; root->size = root->cnt = 1; return root; } Node *now = root, *newnode; while(1) { now->size++; if(val == now->val) { now->cnt++; now->calc_size(); newnode = now; break; } if(val < now->val) { if(now->ls != null) now = now->ls; else { now->ls = &node[++size]; newnode = now->ls; newnode->val = val; newnode->size = newnode->cnt = 1; newnode->ls = newnode->rs = null; newnode->par = now; break; } } else { if(now->rs != null) now = now->rs; else { now->rs = &node[++size]; newnode = now->rs; newnode->val = val; newnode->size = newnode->cnt = 1; newnode->ls = newnode->rs = null; newnode->par = now; break; } } } splay(newnode,null); return newnode; } Node* srch(int val) //查找一个值,返回指针 { if(root == null) return null; Node *now = root, *res = null; while(1) { if(val == now->val) { res = now; break; } if(val > now->val) { if(now->rs != null) now = now->rs; else break; } else { if(now->ls != null) now = now->ls; else break; } } splay(now,null); return res; } Node* srchmin(Node *rt) //查找rt统领的树中最小值 { Node *rtpar = rt->par; Node *now = rt; while(now->ls != null) now = now->ls; splay(now,rtpar); return now; } Node* srchmax(Node *rt) //查找rt统领的树中最大值 { Node *rtpar = rt->par; Node *now = rt; while(now->rs != null) now = now->rs; splay(now,rtpar); return now; } void del(int val) { if(root == null) return; Node *res = srch(val); if(res == null) return; if(res->cnt > 1) { res->cnt--; res->calc_size(); return; } if(res->ls == null && res->rs == null) { this->init(); return; } if(res->ls == null) { root = res->rs; res->rs->par = null; return; } if(res->rs == null) { root = res->ls; res->ls->par = null; return; } Node *z = srchmin(res->rs); //查询后继 z->par = null; z->ls = res->ls; res->ls->par = z; z->calc_size(); root = z; } int getrank(int val) { Node *x = srch(val); if(x == null) return 0; return x->ls->size + 1; //return x->ls->size + cnt; } Node* getkth(int kth) { if(root == null || kth<=0 || kth > root->size) return null; Node *now = root; while(1) { if(now->ls->size + 1 <= kth && kth <= now->ls->size + now->cnt) break; if(now->ls->size + 1 > kth) now = now->ls; else { kth -= now->ls->size + now->cnt; now = now->rs; } } splay(now,null); return now; } }sp; int main() { sp.init(); sp.ins(10); sp.ins(2); sp.ins(2); sp.ins(2); sp.ins(3); sp.ins(3); sp.ins(10); cout<<sp.getrank(2)<<endl; cout<<sp.getrank(3)<<endl; cout<<sp.getrank(10)<<endl; for(int i=1;i<=sp.root->size;i++) cout<<sp.getkth(i)->val<<"\t"; cout<<endl; sp.del(1); sp.del(2); sp.del(3); cout<<sp.getrank(2)<<endl; cout<<sp.getrank(3)<<endl; cout<<sp.getrank(10)<<endl; for(int i=1;i<=sp.root->size;i++) cout<<sp.getkth(i)->val<<"\t"; cout<<endl; return 0; }
5 经典应用 - 区间添加、删除、翻转
根据伸展树中伸展操作不会改变二叉树性质的原理,不难知道对二叉树的splay操作其实不会影响中序遍历二叉树产生的序列,
假设现有一个数字序列,我们用伸展树来维护它,并且中序遍历树所产生的序列就是该序列。
那么对应的序列操作有如下三种:
5.1 区间添加
在当前序列第 $p$ 个元素之后,添加指定序列:
先把第 $p$ 个元素伸展到根,再把第 $p+1$ 个元素伸展到 $x$ 的右子树的根,再把需要插入的序列建成一棵子树,插入到第 $p+1$ 个元素的左子树(原先为空)即可。
5.2 区间删除
删除当前序列第 $x$ 个元素到第 $y$ 个元素:
只需要先把第 $x-1$ 个元素伸展到根,再把第 $y+1$ 个元素伸展到 $x$ 的右子树的根,
此时第 $x$ 个元素到第 $y$ 个元素的序列就会是第 $y+1$ 个元素的左子树,删除即可。
5.3 区间翻转
逆序当前序列中第 $x$ 个元素到第 $y$ 个元素:
借助线段树中经典的标记:lazy标记,
先和5.2节一样,将第 $x-1$ 个元素伸展到根,再把第 $y+1$ 个元素伸展到 $x$ 的右子树的根,
此时第 $x$ 个元素到第 $y$ 个元素的序列就会是第 $y+1$ 个元素的左子树,
再令这棵子树的根节点的lazy = !lazy,若原先lazy = 0,则现在lazy = 1,代表需要翻转,
而当之后访问到该节点时,将该节点的lazy标记下放到左右儿子,并且交换左右儿子即可。
本文主要参考:
①https://wenku.baidu.com/view/a202e27931b765ce05081416.html
②https://blog.csdn.net/leolin_/article/details/6436037



 浙公网安备 33010602011771号
浙公网安备 33010602011771号