POJ 2187 - Beauty Contest - [凸包+旋转卡壳法][凸包的直径]
题目链接:http://poj.org/problem?id=2187
Time Limit: 3000MS Memory Limit: 65536K
Description
Even though Bessie travels directly in a straight line between pairs of farms, the distance between some farms can be quite large, so she wants to bring a suitcase full of hay with her so she has enough food to eat on each leg of her journey. Since Bessie refills her suitcase at every farm she visits, she wants to determine the maximum possible distance she might need to travel so she knows the size of suitcase she must bring.Help Bessie by computing the maximum distance among all pairs of farms.
Input
* Lines 2..N+1: Two space-separated integers x and y specifying coordinate of each farm
Output
Sample Input
4 0 0 0 1 1 1 1 0
Sample Output
2
Hint
题意:
有一头美牛,她要再一个二维平面上,跑遍上面所有的农场(每个农场都有一个坐标,并且农场不重合),她现在想知道任意两个农场中,最大距离的平方是多少?
题解:
一看农场有几座,50000……emmm,看来 $O(n^2)$ 的暴力是肯定跪了的。然后不难发现,两农场间最大距离肯定是出现在凸包边界上的两个点间;
所以我们求出凸包,遍历凸包上的点可以优化时间复杂度。
由于这题时间卡的不紧,那要是数据里面有一个 $50000$ 个点的凸包边界呢?一样要GG。
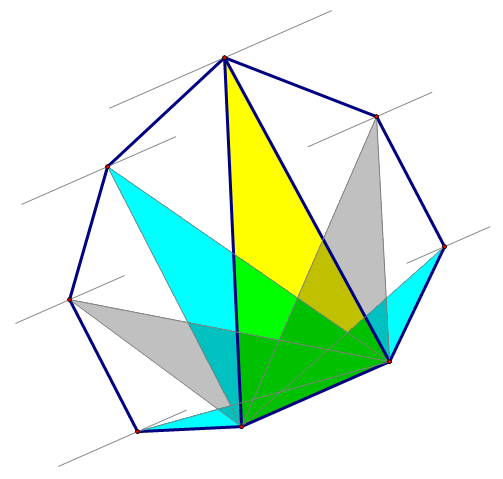
所以,我们有了一种新的方法叫做旋转卡壳法,具体什么个方法,网上有一张很常见的图:

参考关于旋转卡壳的讲解:https://www.cnblogs.com/xdruid/archive/2012/07/01/2572303.html

卡壳的一种情况是这样,两边分别卡着凸包的一条边和一个点。(另一种是同时卡住两个点,这两个点被称为对踵点)
这种情况在实现中比较容易处理,这里就只研究这种情况。
在第二种情况中 我们可以看到一个对踵点和对应边之间的距离比其他点要大。
也就是说,一个对踵点和对应边所形成的三角形面积是最大的,据此可以得到对踵点的简化求法。
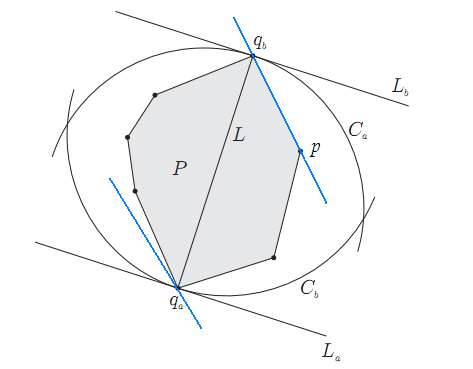
如果 $q_a,q_b$ 分别是凸包上最远的两点,必然可以分别过 $q_a,q_b$ 画出一对平行线(即卡壳)。
然后通过旋转这对平行线,我们可以让它和凸包上的一条边重合,即图中的直线 $(q_a,p)$,可以注意到,此时 $q_a$ 是凸包上离直线 $(q_a,p)$ 最远的点。
于是我们的思路就是:枚举凸包上的所有边,对每一条边找出凸包上离该边最远的顶点,计算这个顶点到该边两个端点的距离,并记录最大的值。
直观上这是一个 $O(n^2)$ 的算法,和直接枚举任意两个顶点一样。
然而我们可以发现,凸包上的点依次与对应边产生的距离成单峰函数:

根据这个凸包的特性,可以注意到,逆时针枚举边的时候,最远点的变化也是逆时针的,这样就可以不用从头计算最远点,而可以紧接着上一次的最远点继续计算。
于是我们得到了 $O(n)$ 的求最远点对的算法:利用旋转卡壳,我们可以在 $O(n)$ 的时间内得到凸包的对踵点中长度最长的点对;又由于最远点对必然属于对踵点对集合,所以用旋转卡壳求出对踵点对集合,然后维护对踵点间最大的距离即可。
代码模板:
double RotatingCalipers(const vector<Point> &ch) //旋转卡壳法 { double ans=0; int sz=ch.size(); for(int i=0,q=1;i<sz;i++) { int j=(i+1)%sz; while( Cross(ch[j]-ch[i],ch[(q+1)%sz]-ch[i]) > Cross(ch[j]-ch[i],ch[q]-ch[i]) ) q=(q+1)%sz; ans=max( ans, max(Length(ch[i],ch[q]),Length(ch[j],ch[q])) ); ans=max( ans, max(Length(ch[i],ch[(q+1)%sz]),Length(ch[j],ch[(q+1)%sz])) ); } return ans; }
其中这么维护最大值的原因是考虑这种情况: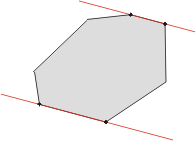
AC代码(在OpenJudge百练2187提交):
#include<bits/stdc++.h> #define mk make_pair #define fi first #define se second #define pb push_back using namespace std; const double eps=1e-8; const double INF=1e18; int Sign(double x) { if(x<-eps) return -1; if(x>eps) return 1; return 0; } int Cmp(double x,double y){return Sign(x-y);} struct Point { double x,y; Point(double _x=0,double _y=0):x(_x),y(_y){} Point operator+(const Point &o)const{return Point(x+o.x,y+o.y);} Point operator-(const Point &o)const{return Point(x-o.x,y-o.y);} Point operator*(double k)const{return Point(x*k,y*k);} Point operator/(double k)const{return Point(x/k,y/k);} int operator==(const Point &o)const{return Cmp(x,o.x)==0 && Cmp(y,o.y)==0;} bool operator<(const Point &o)const { int sgn=Cmp(x,o.x); if(sgn==-1) return 1; else if(sgn==1) return 0; else return Cmp(y,o.y)==-1; } void print(){printf("%.11f %.11f\n",x,y);} }; typedef Point Vctor; //叉积 double Cross(Vctor A,Vctor B){return A.x*B.y-A.y*B.x;} double Cross(Point O,Point A,Point B){return Cross(A-O,B-O);} //距离 double Dot(Vctor A,Vctor B){return A.x*B.x+A.y*B.y;} double Length(Vctor A){return sqrt(Dot(A,A));} double Length(Point A,Point B){return Length(A-B);} vector<Point> ConvexHull(vector<Point> P,int flag=1) //flag=0不严格 flag=1严格 { if(P.size()<=1) return P; int sz=P.size(); vector<Point> ans(2*sz); sort(P.begin(),P.end()); int now=-1; for(int i=0;i<sz;i++) { while(now>0 && Sign(Cross(ans[now]-ans[now-1],P[i]-ans[now-1]))<flag) now--; ans[++now]=P[i]; } int pre=now; for(int i=sz-2;i>=0;i--) { while(now>pre && Sign(Cross(ans[now]-ans[now-1],P[i]-ans[now-1]))<flag) now--; ans[++now]=P[i]; } ans.resize(now); return ans; } double RotatingCalipers(const vector<Point> &P) //旋转卡壳法 { double ans=0; int sz=P.size(); for(int i=0,q=1;i<sz;i++) { int j=(i+1)%sz; while( Cross(P[j]-P[i],P[q]-P[i]) < Cross(P[j]-P[i],P[(q+1)%sz]-P[i]) ) q=(q+1)%sz; ans=max( ans, max(Length(P[i],P[q]),Length(P[j],P[q])) ); ans=max( ans, max(Length(P[i],P[(q+1)%sz]),Length(P[j],P[(q+1)%sz])) ); } return ans; } int n; vector<Point> P; int main() { cin>>n; for(int i=1;i<=n;i++) { double x,y; cin>>x>>y; P.pb(Point(x,y)); } double ans=RotatingCalipers(ConvexHull(P)); printf("%.0f\n",ans*ans); }
PS.用jls给的几何板子更新了一下模板,这里求凸包的方法用的是Jarris步进法,时间复杂度 $O(nH)$,其中 $H$ 是凸包边界上的点数。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号