Codeforces 869 - A/B/C

Rock... Paper!

After Karen have found the deterministic winning (losing?) strategy for rock-paper-scissors, her brother, Koyomi, comes up with a new game as a substitute. The game works as follows.

A positive integer n is decided first. Both Koyomi and Karen independently choose n distinct positive integers, denoted by x1, x2, ..., xnand y1, y2, ..., yn respectively. They reveal their sequences, and repeat until all of 2n integers become distinct, which is the only final state to be kept and considered.

Then they count the number of ordered pairs (i, j) (1 ≤ i, j ≤ n) such that the value xi xor yj equals to one of the 2n integers. Here xormeans the bitwise exclusive or operation on two integers, and is denoted by operators ^ and/or xor in most programming languages.

Karen claims a win if the number of such pairs is even, and Koyomi does otherwise. And you're here to help determine the winner of their latest game.

Input

The first line of input contains a positive integer n (1 ≤ n ≤ 2 000) — the length of both sequences.

The second line contains n space-separated integers x1, x2, ..., xn (1 ≤ xi ≤ 2·106) — the integers finally chosen by Koyomi.

The third line contains n space-separated integers y1, y2, ..., yn (1 ≤ yi ≤ 2·106) — the integers finally chosen by Karen.

Input guarantees that the given 2n integers are pairwise distinct, that is, no pair (i, j) (1 ≤ i, j ≤ n) exists such that one of the following holds: xi = yj; i ≠ j and xi = xj; i ≠ j and yi = yj.

Output

Output one line — the name of the winner, that is, "Koyomi" or "Karen" (without quotes). Please be aware of the capitalization.

Examples

input

3
1 2 3
4 5 6

output

Karen

input

5
2 4 6 8 10
9 7 5 3 1

output

Karen

Note

In the first example, there are 6 pairs satisfying the constraint: (1, 1), (1, 2), (2, 1), (2, 3), (3, 2) and (3, 3). Thus, Karen wins since 6 is an even number.

In the second example, there are 16 such pairs, and Karen wins again.

简单的模拟题；

AC代码：

 1 #include<cstdio>
 2 #include<map>
 3 using namespace std;
 4 int n,num[2][2005];
 5 map<int,int> vis;
 6 int main()
 7 {
 8     scanf("%d",&n);
 9     for(int r=0;r<2;r++) for(int i=1;i<=n;i++) {scanf("%d",&num[r][i]);vis[num[r][i]]=1;}
10     int pair=0;
11     for(int i=1;i<=n;i++)
12     {
13         for(int j=1;j<=n;j++)
14         {
15             if(vis.count(num[0][i]^num[1][j])) pair++;
16         }
17     }
18     if(pair%2) printf("Koyomi\n");
19     else printf("Karen\n");
20 }

View Code

B. The Eternal Immortality

Even if the world is full of counterfeits, I still regard it as wonderful.

Pile up herbs and incense, and arise again from the flames and ashes of its predecessor — as is known to many, the phoenix does it like this.

The phoenix has a rather long lifespan, and reincarnates itself once every a! years. Here a! denotes the factorial of integer a, that is, a! = 1 × 2 × ... × a. Specifically, 0! = 1.

Koyomi doesn't care much about this, but before he gets into another mess with oddities, he is interested in the number of times the phoenix will reincarnate in a timespan of b! years, that is, 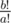$\text{[math]}$ . Note that when b ≥ a this value is always integer.

As the answer can be quite large, it would be enough for Koyomi just to know the last digit of the answer in decimal representation. And you're here to provide Koyomi with this knowledge.

Input

The first and only line of input contains two space-separated integers a and b (0 ≤ a ≤ b ≤ 1018).

Output

Output one line containing a single decimal digit — the last digit of the value that interests Koyomi.

Examples

input

2 4

output

input

0 10

output

input

107 109

output

Note

In the first example, the last digit of 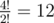$\text{[math]}$ is 2;

In the second example, the last digit of 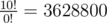$\text{[math]}$ is 0;

In the third example, the last digit of 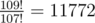$\text{[math]}$ is 2.

简单模拟题，稍微做一些特别的处理即可；

AC代码：

 1 #include<iostream>
 2 using namespace std;
 3 typedef unsigned long long LLU;
 4 LLU n,m;
 5 int main()
 6 {
 7     cin>>n>>m;
 8     int ans=1;
 9     for(LLU i=m;i>n;i--)
10     {
11         ans*=i%10;
12         ans%=10;
13         if(ans==0) break;
14     }
15     cout<<ans;
16 }

View Code

C. The Intriguing Obsession

— This is not playing but duty as allies of justice, Nii-chan!

— Not allies but justice itself, Onii-chan!

With hands joined, go everywhere at a speed faster than our thoughts! This time, the Fire Sisters — Karen and Tsukihi — is heading for somewhere they've never reached — water-surrounded islands!

There are three clusters of islands, conveniently coloured red, blue and purple. The clusters consist of a, b and c distinct islands respectively.

Bridges have been built between some (possibly all or none) of the islands. A bridge bidirectionally connects two different islands and has length 1. For any two islands of the same colour, either they shouldn't be reached from each other through bridges, or the shortest distance between them is at least 3, apparently in order to prevent oddities from spreading quickly inside a cluster.

The Fire Sisters are ready for the unknown, but they'd also like to test your courage. And you're here to figure out the number of different ways to build all bridges under the constraints, and give the answer modulo 998 244 353. Two ways are considered different if a pair of islands exist, such that there's a bridge between them in one of them, but not in the other.

Input

The first and only line of input contains three space-separated integers a, b and c (1 ≤ a, b, c ≤ 5 000) — the number of islands in the red, blue and purple clusters, respectively.

Output

Output one line containing an integer — the number of different ways to build bridges, modulo 998 244 353.

Examples

input

1 1 1

output

input

1 2 2

output

input

1 3 5

output

input

6 2 9

output

813023575

Note

In the first example, there are 3 bridges that can possibly be built, and no setup of bridges violates the restrictions. Thus the answer is 23 = 8.

In the second example, the upper two structures in the figure below are instances of valid ones, while the lower two are invalid due to the blue and purple clusters, respectively.

$\text{[math]}$

题意：

有三堆群岛，分别用不同颜色标记，现在在岛间建桥，桥长度均为1，限制条件：同颜色的岛间距离不小于3或者没有连接，求有多少种建桥方案（结果对998244353取模）。

题解：

对于两堆岛，假设岛堆1有m个岛，岛堆2有n个岛，且满足m<=n，则不难得到两个两堆岛间建立桥的方案数：

$f(m,n)=\sum_{i=0}^{m}C_{m}^{i}A_{n}^{i}=\sum_{i=0}^{m}C_{m}^{i}C_{n}^{i}i!$

关于如何求组合数C(n,m)：http://www.cnblogs.com/xienaoban/p/6798058.html

因为我们看到，a,b,c最大不超过5000，所以可以用迭代的方式求组合数和阶乘；

最后根据公式计算出答案即可；

 1 #include<cstdio>
 2 #include<algorithm>
 3 #define MAX 5003
 4 #define MOD 998244353
 5 using namespace std;
 6 typedef long long ll;
 7 ll C[MAX][MAX],fac[MAX];
 8 void calc_Cmn()//求组合数
 9 {
10     for(int i=0;i<MAX;i++)
11     {
12         C[i][0]=C[i][i]=1;
13         for(int j=1;j<i;j++) C[i][j]=(C[i-1][j-1]+C[i-1][j])%MOD;
14     }
15 }
16 void calc_factorial()//求阶乘
17 {
18     fac[0]=fac[1]=1;
19     for(int i=2;i<MAX;i++) fac[i]=(fac[i-1]*i)%MOD;
20 }
21 ll f(int m,int n)
22 {
23     ll ret=0;
24     for(int i=0;i<=m;i++)
25     {
26         ret+=(((C[m][i]*C[n][i])%MOD)*fac[i])%MOD;
27         ret=ret%MOD;
28     }
29     return ret;
30 }
31 int main()
32 {
33     calc_Cmn();
34     calc_factorial();
35     int x,y,z,m,n;
36     scanf("%d%d%d",&x,&y,&z);
37 
38     m=min(x,y), n=max(x,y);
39     ll ans1=f(m,n);
40     m=min(x,z), n=max(x,z);
41     ll ans2=f(m,n);
42     m=min(y,z), n=max(y,z);
43     ll ans3=f(m,n);
44 
45     printf("%I64d\n",(((ans1*ans2)%MOD)*ans3)%MOD);
46 }

PS.里面包含了求组合数和阶乘的算法模板

posted @ 2017-10-07 16:32 Dilthey 阅读(195) 评论(0) 编辑收藏举报

刷新页面返回顶部

Codeforces 869 - A/B/C

公告