关于反向传播的笔记

参考《ML Lecture 7: Backpropagation》：

 

假设一个比较简单的网络结构如下：

 

 

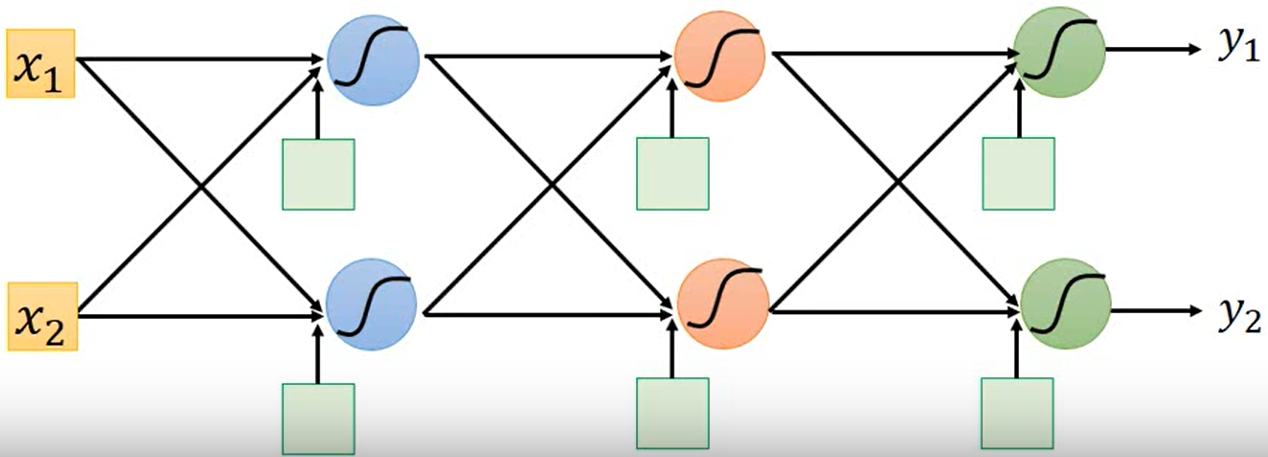
我们取其中一部分做详细的分析：

 

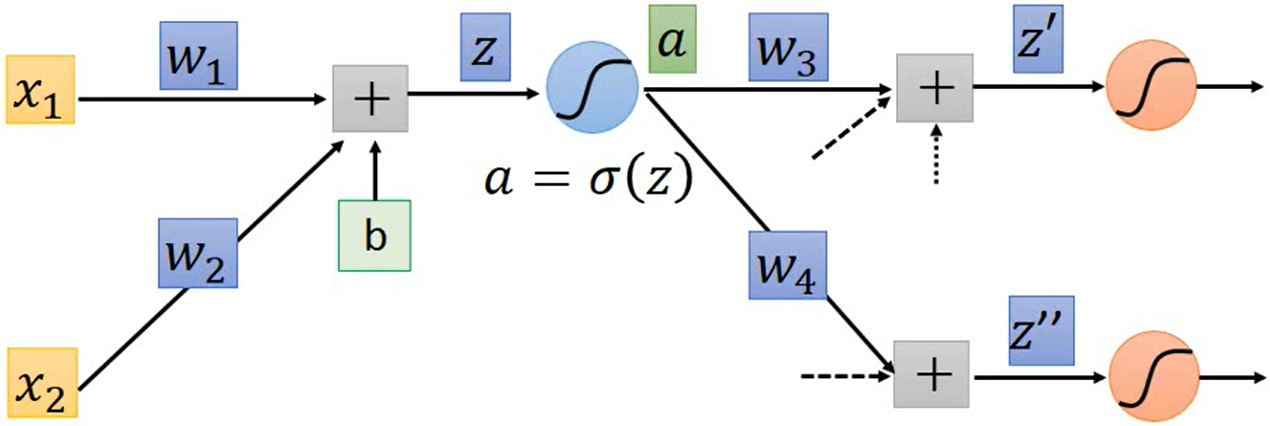
对于一个输入 ${x_1, x_2}$，它能计算出对应的 loss $C(x;\theta)$，我们如果想要更新参数 $\theta = \{w_1, w_2, \cdots, b_1, b_2, \cdots \}$，就要计算 $\nabla_\theta C(\theta)$，即所有的 $\frac{\partial C}{\partial w}, \frac{\partial C}{\partial b}$。

对于上图，第一个神经元的三个参数有

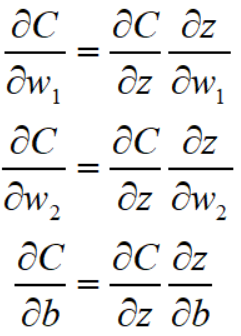
其中 $\frac{\partial C}{\partial z}$ 不好算，但是 $\frac{\partial z}{\partial w_1}, \frac{\partial z}{\partial w_2}, \frac{\partial z}{\partial b}$ 是很好算的

这其实对于所有的神经元都是一样的，某个神经元中的求和结果 $z$ 对于 weight 的偏导就是对应的 input（即这条有向边的起点），对于 bias 的偏导就是 $1$。这就是 forward pass，在参数确定、输入确定的情况下，可以很快的计算出所有的 $\frac{\partial z}{\partial w}, \frac{\partial z}{\partial b}$。

 

然后就是比较难的问题，怎么计算 $\frac{\partial C}{\partial z}$ 呢？

记 $a = \sigma (z)$ 是一个激活函数，就有

而对于 $\frac{\partial C}{\partial a}$ 又有

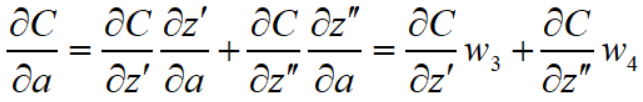
所以计算 $\frac{\partial C}{\partial z}$ 的表达式是这样的

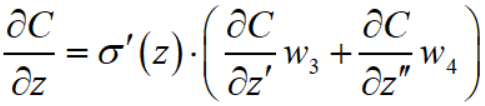
在输入确定的情况下 $\sigma ' (z)$ 就也是确定的（相当于乘一个放缩系数），很明显能看出一种逆推的关系

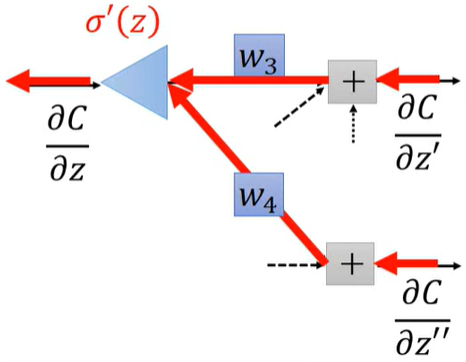
其实这时已经能感受到反向传播的味道了。为了更加易懂，不妨来看看这个网络的最后一层（假设是如下图的参数，$y_1, y_2$ 是网络的输出）

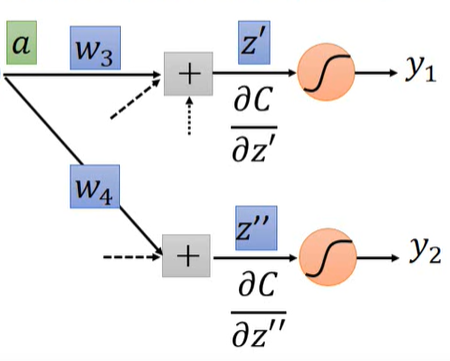
那么就有

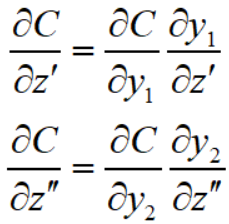
其中 $\frac{\partial C}{\partial y_1}, \frac{\partial C}{\partial y_2}$ 取决于你的函数 $C$，假设你的函数 $C = \sum_{i} y_i^2 = y_1^2 + y_2^2$，那么 $\frac{\partial C}{\partial y_1} = 2y_1, \frac{\partial C}{\partial y_2} = 2y_2$，再把网络的输出，确定的 $y_1, y_2$ 值代入就好了。至于 $\frac{\partial y_1}{\partial z'} = \sigma'(z'), \frac{\partial y_2}{\partial z''} = \sigma'(z'')$ 之前就讲过了，相当于一个确定的放缩系数。

所以，我们就可以从网络的最后一层，往前一层一层地逆推出所有的 $\frac{\partial C}{\partial z}$，这就是 backward pass。

 

这样一来，我们经过一次 forward pass 得到了所有的 $\frac{\partial z}{\partial w}, \frac{\partial z}{\partial b}$，又经过一次 backward pass 得到了所有的 $\frac{\partial C}{\partial z}$，两者相乘就可以得到所有的 $\frac{\partial C}{\partial w}, \frac{\partial C}{\partial b}$，即 $\nabla_\theta C(\theta)$。