关于Wasserstein GAN的一些笔记
这篇笔记基于上一篇《关于GAN的一些笔记》。
1 GAN的缺陷
由于 $P_G$ 和 $P_{data}$ 它们实际上是 high-dim space 中的 low-dim manifold,因此 $P_G$ 和 $P_{data}$ 之间几乎是没有重叠的
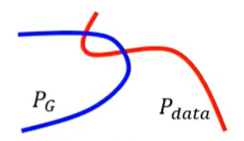
正如我们之前说的,如果两个分布 $P,Q$ 完全没有重叠,那么 JS divergence 是一个常数 $\log(2)$。
由于最优的 generator 是
![]()
我们在普通的 GAN 中,最小化的是 $P_{data}$ 和 $P_G$ 之间的 JS divergence,那么由于 $P_G$ 和 $P_{data}$ 之间几乎是没有重叠的,所以往往会导致 $P_G$ 和 $P_{data}$ 之间的 JS divergence 接近于 $\log(2)$。
由于无法判别到底那种情况下两个分布更加接近,这就意味着有时候普通的 GAN 很难训练,甚至没法训练。
而如果我们采用实际代码实现中的 NSGAN,即把 generator 的 loss 改成
![]()
首先请注意,我们训练 generator 时,discriminator 是固定的,不妨记作 $D^{*}$,而 $D^{*} = P_{data}(x) / (P_{data}(x) + P_G(x))$,这里的 $P_G$ 是还未更新的 generator $G$ 所对应的 distribution。
由于我们已知(详细的推导可以参见《关于GAN的一些笔记》)
![]()
类似的我们也可以把 KL divergence 写成
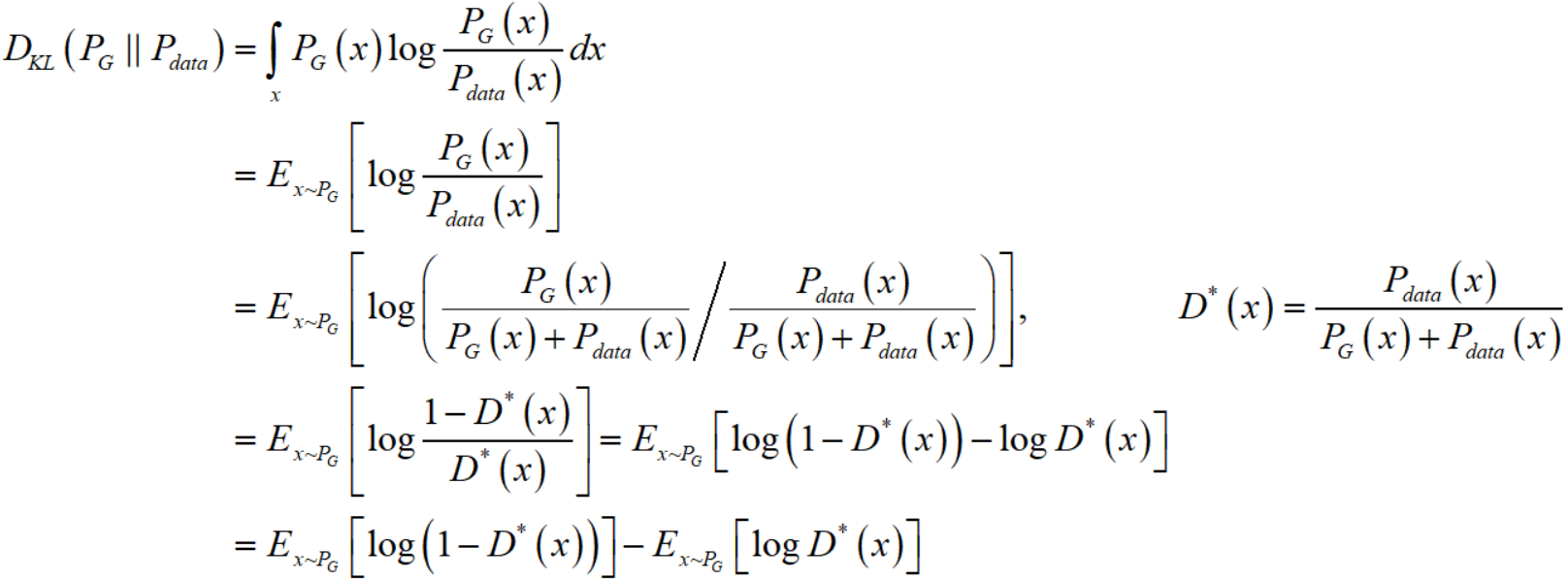
所以
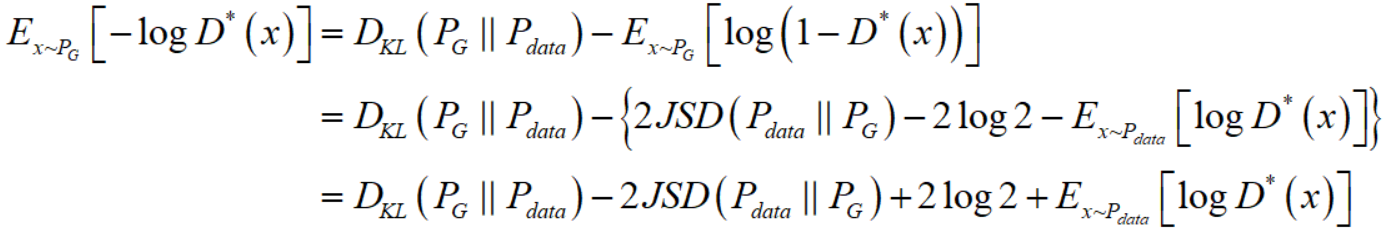
注意到对于后两项,一项是常数项,一项是更改 $G$ 无法影响的(当你训练 $G$ 时,$D$ 是固定的,同时 $P_{data}$ 显然也是不会变的)。所以,你如果把 generator 的 loss 改成了 $V = E_{x \sim P_G}[-\log D(x)]$,那么你就相当于在寻找最优的 generator
![]()
这显然在理论上是站不住脚的,一边想使得两个分布的 KL divergence 尽量小,一边又想要使得两个分布的 JS divergence 尽量大,这是矛盾的。这在数值上则会导致梯度不稳定,这就是后面那个 JS divergence 所带来的问题。
而且另外一个问题是 KL divergence 是非对称的,会带来以下问题:
首先写出 $D_{KL}(P_G \parallel P_{data}) = \int_{x} P_G(x)\log \frac{P_G(x)}{P_{data}(x)}dx$,我们分两种情况考虑 generator $G$ 会犯的错误:
① 对于某处的 $x$,$P_G(x)$ 是高概率(接近 $1$)而 $P_{data}(x)$ 是低概率(接近 $0$),那么此时 $P_G(x)\log \frac{P_G(x)}{P_{data}(x)}$ 接近于正无穷,对于 $D_{KL}(P_G \parallel P_{data})$ 产生了巨大的贡献。
② 对于某处的 $x$,$P_G(x)$ 是低概率(接近 $0$)而 $P_{data}(x)$ 是高概率(接近 $1$),那么此时 $P_G(x)\log \frac{P_G(x)}{P_{data}(x)}$ 接近于 $0$,对于 $D_{KL}(P_G \parallel P_{data})$ 产生了微乎其微的贡献。
这就导致了,对于错误①(generator 生成了不符合 $P_{data}$ 的错误图片)惩罚巨大,而对于错误② (generator 没有尽可能生成符合 $P_{data}$ 的正确图片)惩罚很小。这就是的 generator $G$ 会多生成一些重复的但是符合 $P_{data}$ 的正确图片,而不愿意去生成多样性的样本,因为那样就很容易产生错误①,会受到巨大的惩罚。这种现象就是大家常说的 collapse mode。这应该就是《关于GAN的一些笔记》中生成结果中有大量的“$1$”的原因。
2 WGAN
之前在《关于GAN的一些笔记》中写到了 Wasserstein distance 相较于 JS/KL divergence 的优越性。就算 $P_G, P_{data}$ 之间没有重叠也可以衡量两个分布的距离。
当然,$W(P,Q) = \inf\limits_{\gamma \in \Pi(P_{data},P_G)} E_{(x,y) \sim \gamma}[\left \| x-y \right \|]$ 这种形式没法直接变换得到objective function。但是可以用一个定理将其变换成如下形式
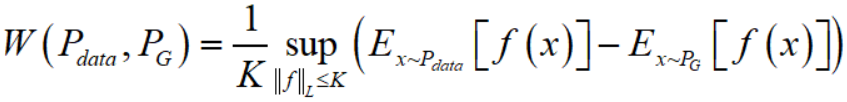
这里需要用到的一个知识是 Lipschitz 连续,它对一个函数 $f$ 施加一个限制,要求存在一个常数 $K$ 使得 $f$ 的定义域内任意的两个元素 $x_1, x_2$ 都满足
![]()
形象一点的描述就是迫使函数不能过分陡峭,此时成函数 $f$ 的 Lipschitz 常数为 $K$。
所以,变换后的 Wasserstein distance 的意思就是在要求函数 $f$ 的 Lipschitz 常数 $\left \| f \right \|_{L}$ 不超过 $K$ 的条件下,对所有可能满足条件的 $f$ 取到 $E_{x \sim P_{data}}[f(x)] - E_{x \sim P_G}[f(x)]$ 的上界,然后再除以 $K$。假设我们有一组参数 $w$ 来定义函数 $f_w$,那么 Wasserstein distance 可以近似表达成
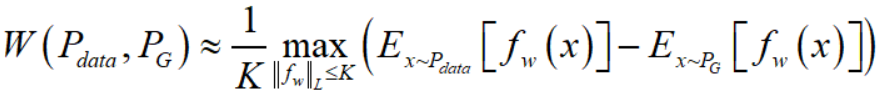
回到 GAN 本身,我们知道训练 generator $G$ 的目的是减小 $P_{data},P_G$ 之间的距离,而训练 discriminator $D$ 的目的是量出 $P_{data},P_G$ 之间的距离。那么对于 generator $G$ 有
![]()
而 discriminator $D$ 就是要在给定 $G$ 的条件下,量取此时的 $W(P_{data}, P_G)$,参考上面 Wasserstein distance 的近似式,以及 network 强大的函数拟合能力(由于现在 $D$ 做的是近似拟合 Wasserstein distance 属回归任务,而非分类任务,所以要把最后一层的sigmoid拿掉),我们的 discriminator $D$ 自然而然就是令
![]()
尽可能地取到最大值,此时的 $V$ 即约等于 $W(P_{data}, P_G)$。
需要注意的点是,对于函数 $D(x)$ 是有限制的,即要存在一个常数 $K$ 使得 $\left \| D \right \|_{L} \leq K$, 这其实很简单,我们只要使得 network $D$ 的任意一个参数 $w_i$ 都在一个区间 $[-c,c]$ 以内, 此时肯定会使得梯度 $\nabla_{x}D(x)$ 不会大于某一个常数,也就使得 $D$ 满足了 $\left \| D \right \|_{L} \leq K$。而在具体实现中,只需要在更新完 $D$ 的参数后,做一个weight clipping。即若 $w_i > c$ 则 $w_i := c$,若 $w_i < -c$ 则 $w_i := -c$。
所以综上,对于 $D$ 有loss function
![]()
加负号是因为loss function一般是越小越好。
而对于 $G$ 有loss function
![]()
可以去掉第一项是因为 $E_{x\sim P_{data}}[D(x)]$ 不受 $G$ 的变动影响。
最后总结,WGAN与原始GAN的区别就以下四点
- discriminator 最后一层去掉 $\rm{sigmoid}$;
- generator 和 discriminator 的 loss 不取 $\log$;
- 每次更新 discriminator 的参数之后把它们的绝对值截断至不超过一个固定常数 $c$;
- 不要用基于动量的优化算法(包括 momentum 和 Adam),推荐 RMSProp,SGD 也行(这点是作者从实验中发现的,属于trick。作者发现如果使用 Adam,discriminator 的 loss 有时候会崩掉,当它崩掉时,Adam 给出的更新方向与梯度方向夹角的 $\cos$ 值就变成负数,更新方向与梯度方向南辕北辙,这意味着 discriminator 的 loss 梯度是不稳定的,所以不适合用Adam这类基于动量的优化算法)。
代码
这个代码是来自https://github.com/eriklindernoren/PyTorch-GAN/blob/master/implementations/wgan/wgan.py
import argparse import os import numpy as np import math import sys import torchvision.transforms as transforms from torchvision.utils import save_image from torch.utils.data import DataLoader from torchvision import datasets from torch.autograd import Variable import torch.nn as nn import torch.nn.functional as F import torch os.makedirs("images", exist_ok=True) parser = argparse.ArgumentParser() parser.add_argument("--n_epochs", type=int, default=200, help="number of epochs of training") parser.add_argument("--batch_size", type=int, default=64, help="size of the batches") parser.add_argument("--lr", type=float, default=0.00005, help="learning rate") parser.add_argument("--n_cpu", type=int, default=8, help="number of cpu threads to use during batch generation") parser.add_argument("--latent_dim", type=int, default=100, help="dimensionality of the latent space") parser.add_argument("--img_size", type=int, default=28, help="size of each image dimension") parser.add_argument("--channels", type=int, default=1, help="number of image channels") parser.add_argument("--n_critic", type=int, default=5, help="number of training steps for discriminator per iter") parser.add_argument("--clip_value", type=float, default=0.01, help="lower and upper clip value for disc. weights") parser.add_argument("--sample_interval", type=int, default=400, help="interval betwen image samples") opt = parser.parse_args() print(opt) img_shape = (opt.channels, opt.img_size, opt.img_size) cuda = True if torch.cuda.is_available() else False print('CUDA is available: ', cuda) class Generator(nn.Module): def __init__(self): super(Generator, self).__init__() def block(in_feat, out_feat, normalize=True): layers = [nn.Linear(in_feat, out_feat)] if normalize: layers.append(nn.BatchNorm1d(out_feat, 0.8)) layers.append(nn.LeakyReLU(0.2, inplace=True)) return layers self.model = nn.Sequential( *block(opt.latent_dim, 128, normalize=False), *block(128, 256), *block(256, 512), *block(512, 1024), nn.Linear(1024, int(np.prod(img_shape))), nn.Tanh() ) def forward(self, z): img = self.model(z) return img.view(img.shape[0], *img_shape) class Discriminator(nn.Module): def __init__(self): super(Discriminator, self).__init__() self.model = nn.Sequential( nn.Linear(int(np.prod(img_shape)), 512), nn.LeakyReLU(0.2, inplace=True), nn.Linear(512, 256), nn.LeakyReLU(0.2, inplace=True), nn.Linear(256, 1) ) def forward(self, img): img_flat = img.view(img.shape[0], -1) return self.model(img_flat) # Initialize generator and discriminator G = Generator() D = Discriminator() if cuda: G.cuda() D.cuda() # Configure data loader os.makedirs("../../data/mnist", exist_ok=True) dataloader = torch.utils.data.DataLoader( datasets.MNIST( "../../data/mnist", train=True, download=True, transform=transforms.Compose([transforms.ToTensor(), transforms.Normalize([0.5], [0.5])]), ), batch_size=opt.batch_size, shuffle=True, ) # Optimizers optimizer_G = torch.optim.RMSprop(G.parameters(), lr=opt.lr) optimizer_D = torch.optim.RMSprop(D.parameters(), lr=opt.lr) Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor batches_done = 0 for epoch in range(opt.n_epochs): for i, (imgs, _) in enumerate(dataloader): # Configure input real_imgs = imgs.type(Tensor) # --------------------- # Train Discriminator # --------------------- # Sample noise as generator input z = Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))) # Generate a batch of images fake_imgs = G(z) # Adversarial loss loss_D = -torch.mean(D(real_imgs)) + torch.mean(D(fake_imgs)) optimizer_D.zero_grad() loss_D.backward() optimizer_D.step() # Clip weights of discriminator for p in D.parameters(): p.data.clamp_(-opt.clip_value, opt.clip_value) # Train the generator every n_critic iterations if i % opt.n_critic == 0: # ----------------- # Train Generator # ----------------- # Generate a batch of images fake_imgs = G(z) # Adversarial loss loss_G = -torch.mean(D(fake_imgs)) optimizer_G.zero_grad() loss_G.backward() optimizer_G.step() print( "[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]" % (epoch + 1, opt.n_epochs, i, len(dataloader), loss_D.item(), loss_G.item()) ) if batches_done % opt.sample_interval == 0: save_image(fake_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True) batches_done += opt.n_critic
运行结果



看起来似乎不是很好。
3 WGAN的进一步优化
3.1 WGAN存在的问题
WGAN-GP 是针对 WGAN 的存在的问题提出来的,WGAN 在真实的实验过程中依旧存在着训练困难、收敛速度慢的问题,相比较传统GAN在实验上提升不是很明显。
WGAN-GP 在文章中指出了 WGAN 存在问题的原因,那就是 WGAN 在处理 Lipschitz 限制条件时直接采用了 weight clipping。通过在训练过程中保证 discriminator 的所有参数处于 $[-c,c]$ 的范围内,保证了 discriminator 不能对两个略微不同的样本在判别上差异过大,从而间接实现 Lipschitz 限制。
实际训练中 discriminator 希望尽可能拉大真假样本的分数差,然而 weight clipping 独立地限制每一个网络参数的取值范围,在这种情况下最优的策略就是尽可能让所有参数走极端,要么取最大值($c$)要么取最小值($-c$),文章通过实验验证了猜测如下图所示判别器的参数几乎都集中在最大值和最小值上。
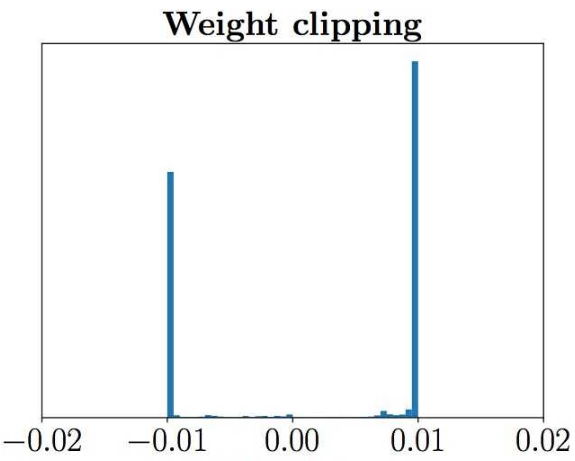
另一个问题就是 weight clipping 会很容易导致梯度消失或者梯度爆炸。原因是 discriminator 是一个多层网络,如果把 weight clipping threshold 设得稍微小了一点,每经过一层网络,梯度就变小一点点,多层之后就会指数衰减;反之,如果设得稍微大了一点,每经过一层网络,梯度变大一点点,多层之后就会指数爆炸。
只有设得不大不小,才能让生成器获得恰到好处的回传梯度,然而在实际应用中这个平衡区域可能很狭窄,就会给调参工作带来麻烦。文章也通过实验展示了这个问题,下图中横轴代表判别器从低到高第几层,纵轴代表梯度回传到这一层之后的尺度大小
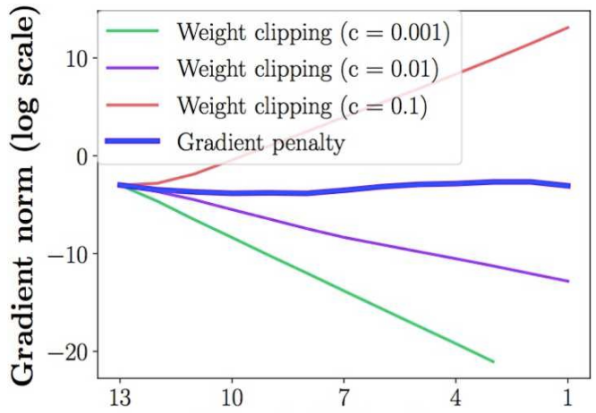
3.2 WGAN-GP
针对以上问题,WGAN-GP 作者提出了解决方案,即 gradient penalty。Lipschitz 限制是要求 discriminator 的梯度不超过 $K$,gradient penalty 就是给 loss 添加一个额外的惩罚项来控制梯度与 $K$ 之间的关系,这就是 gradient penalty 的核心所在。
首先将 Wasserstein distance 的 WGAN 的近似表达式
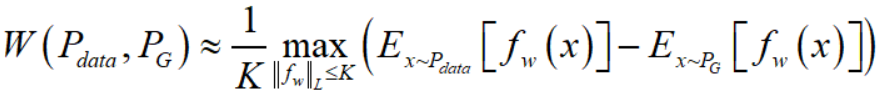
变成
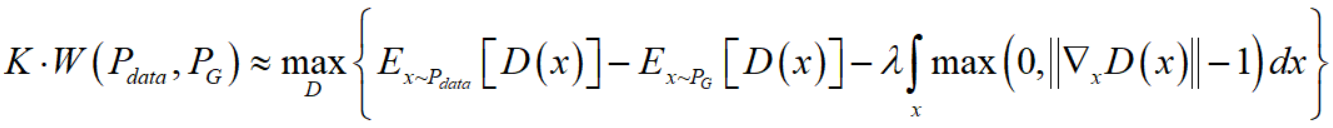
因为 $D \in 1-Lipschitz$ 等价于对于 $\forall x$ 都有 $\left \| \nabla_x D(x) \right \| \leq 1$,所以上式中的惩罚项就是对于 $\left \| \nabla_x D(x) \right \| > 1$ 的情况进行惩罚。
但显然我们依然不可能检查所有的 $x$ 是否 $\left \| \nabla_x D(x) \right \| > 1$,因此继续进行近似
![]()
我们既然不可能检查所有的 $x$,那我们只检查服从分布 $P_{penalty}$(一个事先确定好的分布)的 $x$ 总可以吧。我们尽量让这部分的 $x$ 的 $\left \| \nabla_x D(x) \right \| \leq 1$。
而我们如何去从 $P_{penalty}$ 中采样 $x$ 呢,做法是,对任意的服从 $P_{data}$ 的 $x$ 和服从 $P_G$ 的 $x$ 之间连一条边,在这条边上随机采样,即作为服从 $P_{penalty}$ 的 $x$
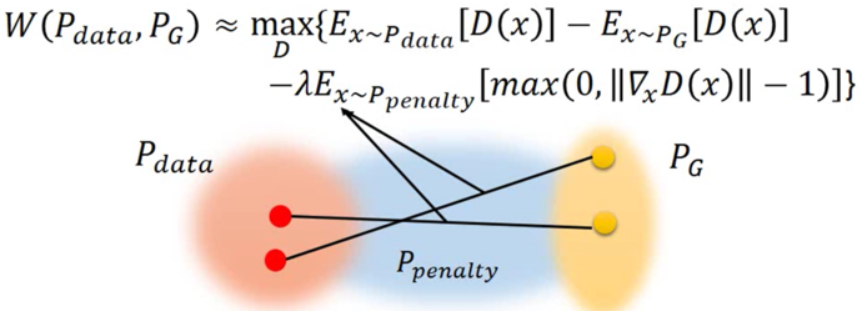
换句话说,我们只限制 $P_{data}$ 和 $P_G$ 之间的区域上 $x$ 的梯度,因为随着训练进行 $P_G$ 是逐渐靠近 $P_{data}$ 的。
然后文章的作者通过实验发现,在实际实现中,如下近似效果更好:
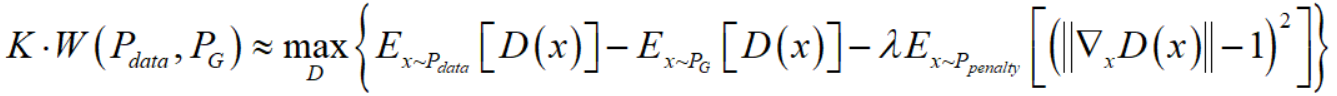
原本是仅仅惩罚 $\left \| \nabla_x D(x) \right \| > 1$ 的情况,现在是 $\left \| \nabla_x D(x) \right \| < 1$ 以及 $\left \| \nabla_x D(x) \right \| > 1$ 都惩罚。
所以,最终的 loss function是
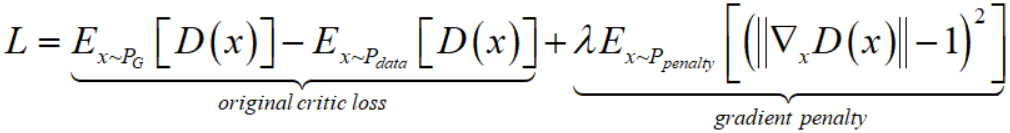
代码
这个代码来自https://github.com/eriklindernoren/PyTorch-GAN/blob/master/implementations/wgan_gp/wgan_gp.py
import argparse import os import numpy as np import math import sys import torchvision.transforms as transforms from torchvision.utils import save_image from torch.utils.data import DataLoader from torchvision import datasets from torch.autograd import Variable import torch.nn as nn import torch.nn.functional as F import torch.autograd as autograd import torch os.makedirs("images", exist_ok=True) parser = argparse.ArgumentParser() parser.add_argument("--n_epochs", type=int, default=200, help="number of epochs of training") parser.add_argument("--batch_size", type=int, default=64, help="size of the batches") parser.add_argument("--lr", type=float, default=0.0002, help="adam: learning rate") parser.add_argument("--b1", type=float, default=0.5, help="adam: decay of first order momentum of gradient") parser.add_argument("--b2", type=float, default=0.999, help="adam: decay of first order momentum of gradient") parser.add_argument("--n_cpu", type=int, default=8, help="number of cpu threads to use during batch generation") parser.add_argument("--latent_dim", type=int, default=100, help="dimensionality of the latent space") parser.add_argument("--img_size", type=int, default=28, help="size of each image dimension") parser.add_argument("--channels", type=int, default=1, help="number of image channels") parser.add_argument("--n_critic", type=int, default=5, help="number of training steps for discriminator per iter") parser.add_argument("--clip_value", type=float, default=0.01, help="lower and upper clip value for disc. weights") parser.add_argument("--sample_interval", type=int, default=400, help="interval betwen image samples") opt = parser.parse_args() print(opt) img_shape = (opt.channels, opt.img_size, opt.img_size) cuda = True if torch.cuda.is_available() else False class Generator(nn.Module): def __init__(self): super(Generator, self).__init__() def block(in_feat, out_feat, normalize=True): layers = [nn.Linear(in_feat, out_feat)] if normalize: layers.append(nn.BatchNorm1d(out_feat, 0.8)) layers.append(nn.LeakyReLU(0.2, inplace=True)) return layers self.model = nn.Sequential( *block(opt.latent_dim, 128, normalize=False), *block(128, 256), *block(256, 512), *block(512, 1024), nn.Linear(1024, int(np.prod(img_shape))), nn.Tanh() ) def forward(self, z): img = self.model(z) img = img.view(img.shape[0], *img_shape) return img class Discriminator(nn.Module): def __init__(self): super(Discriminator, self).__init__() self.model = nn.Sequential( nn.Linear(int(np.prod(img_shape)), 512), nn.LeakyReLU(0.2, inplace=True), nn.Linear(512, 256), nn.LeakyReLU(0.2, inplace=True), nn.Linear(256, 1), ) def forward(self, img): img_flat = img.view(img.shape[0], -1) validity = self.model(img_flat) return validity # Loss weight for gradient penalty lambda_gp = 10 # Initialize generator and discriminator G = Generator() D = Discriminator() if cuda: G.cuda() D.cuda() # Configure data loader os.makedirs("../../data/mnist", exist_ok=True) dataloader = torch.utils.data.DataLoader( datasets.MNIST( "../../data/mnist", train=True, download=True, transform=transforms.Compose( [transforms.Resize(opt.img_size), transforms.ToTensor(), transforms.Normalize([0.5], [0.5])] ), ), batch_size=opt.batch_size, shuffle=True, ) # Optimizers optimizer_G = torch.optim.Adam(G.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2)) optimizer_D = torch.optim.Adam(D.parameters(), lr=opt.lr, betas=(opt.b1, opt.b2)) Tensor = torch.cuda.FloatTensor if cuda else torch.FloatTensor def compute_gradient_penalty(D, real_samples, fake_samples): """Calculates the gradient penalty loss for WGAN GP""" # Random weight term for interpolation between real and fake samples alpha = Tensor(np.random.random((real_samples.size(0), 1, 1, 1))) # Get random interpolation between real and fake samples interpolates = (alpha * real_samples + ((1 - alpha) * fake_samples)).requires_grad_(True) d_interpolates = D(interpolates) fake = Variable(Tensor(real_samples.shape[0], 1).fill_(1.0), requires_grad=False) # Get gradient w.r.t. interpolates gradients = autograd.grad( outputs=d_interpolates, inputs=interpolates, grad_outputs=fake, create_graph=True, retain_graph=True, only_inputs=True, )[0] gradients = gradients.view(gradients.size(0), -1) gradient_penalty = ((gradients.norm(2, dim=1) - 1) ** 2).mean() return gradient_penalty # ---------- # Training # ---------- batches_done = 0 for epoch in range(opt.n_epochs): for i, (imgs, _) in enumerate(dataloader): # Configure input real_imgs = imgs.type(Tensor) # --------------------- # Train Discriminator # --------------------- # Sample noise as generator input z = Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim))) # Generate a batch of images fake_imgs = G(z) # Gradient penalty gradient_penalty = compute_gradient_penalty(D, real_imgs.data, fake_imgs.data) # Adversarial loss d_loss = -torch.mean(D(real_imgs)) + torch.mean(D(fake_imgs)) + lambda_gp * gradient_penalty optimizer_D.zero_grad() d_loss.backward() optimizer_D.step() # Train the generator every n_critic steps if i % opt.n_critic == 0: # ----------------- # Train Generator # ----------------- # Generate a batch of images fake_imgs = G(z) # Loss measures generator's ability to fool the discriminator # Train on fake images g_loss = -torch.mean(D(fake_imgs)) optimizer_G.zero_grad() g_loss.backward() optimizer_G.step() print( "[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]" % (epoch + 1, opt.n_epochs, i, len(dataloader), d_loss.item(), g_loss.item()) ) if batches_done % opt.sample_interval == 0: save_image(fake_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True) batches_done += opt.n_critic
运行结果




看起来是比 WGAN 要好。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号