Codeforces 1099F - Cookies - [DFS+博弈+线段树]
题目链接:https://codeforces.com/problemset/problem/1099/F
Mitya and Vasya are playing an interesting game. They have a rooted tree with $n$ vertices, and the vertices are indexed from $1$ to $n$. The root has index $1$. Every other vertex $i≥2$ has its parent $p_i$, and vertex $i$ is called a child of vertex $p_i$.
There are some cookies in every vertex of the tree: there are $x_i$ cookies in vertex $i$. It takes exactly $t_i$ time for Mitya to eat one cookie in vertex $i$. There is also a chip, which is initially located in the root of the tree, and it takes $l_i$ time to move the chip along the edge connecting vertex $i$ with its parent.
Mitya and Vasya take turns playing, Mitya goes first.
Mitya moves the chip from the vertex, where the chip is located, to one of its children.
Vasya can remove an edge from the vertex, where the chip is located, to one of its children. Vasya can also decide to skip his turn.
Mitya can stop the game at any his turn. Once he stops the game, he moves the chip up to the root, eating some cookies along his way. Mitya can decide how many cookies he would like to eat in every vertex on his way. The total time spent on descend, ascend and eating cookies should not exceed $T$. Please note that in the end of the game the chip is always located in the root of the tree: Mitya can not leave the chip in any other vertex, even if he has already eaten enough cookies — he must move the chip back to the root (and every move from vertex $v$ to its parent takes $l_v$ time).
Find out what is the maximum number of cookies Mitya can eat, regardless of Vasya's actions.
Input
The first line contains two integers $n$ and $T$ — the number of vertices in the tree and the time he has to accomplish his task $(2≤n≤10^5; 1≤T≤10^{18})$.
The second line contains $n$ integers $x_1, x_2, ..., x_n$ — number of cookies located in the corresponding vertex $(1≤x_i≤10^6)$. The third line contains $n$ integers $t_1, t_2, ..., t_n$ — how much time it takes Mitya to eat one cookie in vertex $i$ $(1≤t_i≤10^6)$.
Each of the following $n-1$ lines describe the tree. For every $i$ from $2$ to $n$, the corresponding line contains two integers $p_i$ and $l_i$, where $p_i$ denotes the parent of vertex $i$ and $l_i$ denotes the time it takes Mitya to move the chip along the edge from vertex $i$ to its parent $(1≤p_i<i, 0≤l_i≤10^9)$.
Output
Output a single integer — maximum number of cookies Mitya can eat.
Examples
Input
5 26
1 5 1 7 7
1 3 2 2 2
1 1
1 1
2 0
2 0
Output
11
Input
3 179
2 2 1
6 6 6
1 3
2 3
Output
4
Note
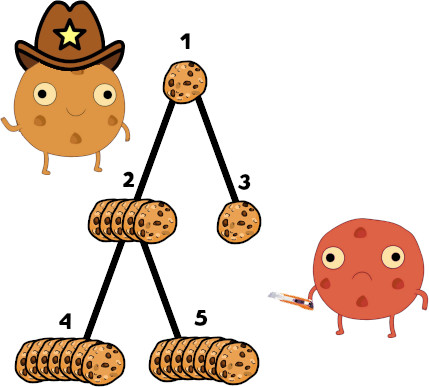
In the first example test case, Mitya can start by moving the chip to vertex 2. In this case no matter how Vasya plays, Mitya is able to eat at least 11 cookies. Below you can find the detailed description of the moves:
Mitya moves chip to vertex $2$.
Vasya removes edge to vertex $4$.
Mitya moves chip to vertex $5$.
Since vertex $5$ has no children, Vasya does not remove any edges.
Mitya stops the game and moves the chip towards the root, eating cookies along the way ($7$ in vertex $5$, $3$ in vertex $2$, $1$ in vertex $1$).
Mitya spend $1+0$ time to go down, $0+1$ to go up, $7⋅2$ to eat $7$ cookies in vertex $5$, $3⋅3$ to eat $3$ cookies in vertex $2$, $1⋅1$ to eat $1$ cookie in vertex $1$. Total time is $1+0+0+1+7⋅2+3⋅3+1⋅1=26$.
题意:
给你一棵树,每个节点上有若干饼干,并且给出每个节点上吃一块饼干需要多少时间,同时给出走过一条边所需时间。
总时限为 $T$,两个人轮流进行操作:
Mitya从当前节点选择一个子节点向下走,或者直接结束游戏并往根回动吃饼干;
Vasya割断当前节点到其某个子节点的边,或者什么都不做。
问Mitya可以吃到的最多的多少块饼干。
题解:
假如我确定某个节点作为终点,那么我就可以得到一条链,走路的时间是固定的,那么要尽量多吃饼干,显然是尽量吃耗时短的饼干。
那么我们可以很容易就可以想到搞一个类似于树上DP的思想来做,某个节点 $x$ 的 $dp[x]$ 就代表在整棵 $tree(x)$ 中选取某个节点作为终点,能吃到的最多饼干数目。
这样一来,就有 $dp[x] = \max[ calc(x), \max_{edge(x,y)}(dp[y]) ]$,其中 $calc(x)$ 就是以节点 $x$ 为终点,能吃到的做多饼干数目。
当然,由于是博弈,因此对于 $\max_{edge(x,y)}(dp[y])$,使得 $dp[y]$ 最大的那条边 $edge(x,y)$ 会被Vasya割断,因此要选择次大的 $dp[y]$。
这样一来,问题就变成了怎么求 $calc(x)$。显然,如果用朴素的做法求 $calc(x)$,是会T的,应当进行一定的优化。
考虑建立一棵线段树,以每个节点吃一块饼干所需的时间作为下标,维护饼干数目以及吃完所有饼干所需时间。这样一来可以 $O(logN)$ 得到 $calc(x)$。
AC代码:
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int maxn=1e5+5; const int maxt=1e6+5; int n; ll T; struct Vtx{ int x,t; }vtx[maxn]; struct Edge{ int v; ll w; }; vector<Edge> E[maxn]; #define ls (rt<<1) #define rs (rt<<1|1) struct Node{ int l,r; ll num,sum; }node[maxt<<2]; void pushup(int rt) { node[rt].num=node[ls].num+node[rs].num; node[rt].sum=node[ls].sum+node[rs].sum; } void build(int rt,int l,int r) { node[rt].l=l, node[rt].r=r; if(l==r) { node[rt].num=node[rt].sum=0; return; } int mid=(l+r)>>1; build(ls,l,mid); build(rs,mid+1,r); pushup(rt); } void update(int rt,int pos,ll val) { if(node[rt].l==node[rt].r) { node[rt].num+=val; node[rt].sum+=val*pos; return; } int mid=(node[rt].l+node[rt].r)>>1; if(pos<=mid) update(ls,pos,val); if(pos>mid) update(rs,pos,val); pushup(rt); } ll query(int rt,ll val) { if(node[rt].l==node[rt].r) return min(node[rt].num,val/node[rt].l); if(val<node[ls].sum) return query(ls,val); else return node[ls].num+query(rs,val-node[ls].sum); } ll dfs(int u,ll rest) { update(1,vtx[u].t,vtx[u].x); ll res=query(1,rest); ll mx1=0, mx2=0; for(auto e:E[u]) { if(2*e.w>=rest) continue; int v=e.v; ll t=dfs(v,rest-2*e.w); if(t>mx1) mx2=mx1, mx1=t; else if(t>mx2) mx2=t; } update(1,vtx[u].t,-vtx[u].x); if(u==1) return max(res,mx1); else return max(res,mx2); } int main() { scanf("%d%I64d",&n,&T); for(int i=1;i<=n;i++) scanf("%d",&vtx[i].x); for(int i=1;i<=n;i++) scanf("%d",&vtx[i].t); for(int i=2;i<=n;i++) { int u; ll w; scanf("%d%I64d",&u,&w); E[u].push_back((Edge){i,w}); } build(1,1,1e6); cout<<dfs(1,T)<<endl; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号