matlab 直方图均衡化

原理：

直方图均衡化首先是一种灰度级变换的方法：

原来的灰度范围[r₀,r_k]变换到[s₀,s_k]变换函数为：s=T(r);

为便于实现，可以用查找表（look-up table）的方式存储，即：原始的灰度作为查找表的索引，表中的内容是新的灰度值。

 

其次，直方图均衡化是图像增强的一种基本方法，可提高图像的对比度，即：将较窄的图像灰度范围以一定规则拉伸至较大（整个灰度级范围内）的范围。

目的是在得到在整个灰度级范围内具有均匀分布的图像。

所以，当输入：直方图H(r)【此处指每个灰度级占有的像素数】;灰度级范围[r₀,r_k]；目的是找到一个s=T(r)使得输出图像的直方图G（s）【同指】在整个灰度级范围内均匀分布。且需满足

（1）0—L(灰度范围)单调递增，避免黑白颠倒；

（2）0<r<L,时0<s<L，保持动态范围一致。

累积分布函数满足这几个要求。

$$\sum\limits_{i = 0}^k {G({s_i})}  = \sum\limits_{j = 0}^k {H({r_j})}$$

 若图像有M*N个像素，则均衡化后的直方图G（q）就有均匀分布：

$$F = \frac{{NM}}{{{s_k} - {s_0}}}$$

代入上式：

$$NM\int\limits_{{s_0}}^s {\frac{1}{{{s_k} - {s_0}}}} ds = \frac{{NM(s - {s_0})}}{{{s_k} - {s_0}}} = \int\limits_{{r_0}}^r {H(r)} dr$$

则：

$$s = T(r) = \frac{{{s_k} - {s_0}}}{{NM}}\int\limits_{{r_0}}^r {H(r)} dr + {s_0}$$

转换成离散形式：

  $$s = T(r) = \frac{{{s_k} - {s_0}}}{{NM}}\sum\limits_{{r_0}}^r {H(r)}  + {s_0}$$

一般 $${s_k} = 255,{s_0} = 0$$

自此就得到了与r相应的s。

---

 

matlab代码：

[filename,pathname]=uigetfile('*.*','select an image');
input_I=imread([pathname filename]);%读入图像

subplot(3,3,1);imshow(input_I);                                 
title('原始图像');%显示原始图像

I_gray = rgb2gray(input_I);
subplot(3,3,4);imshow(I_gray);                                 
title('灰度图像');
subplot(3,3,5);imhist(I_gray);
title('灰度图像直方图');%显示灰度图像及直方图

[height,width]=size(I_gray);

r=zeros(1,256);
for i=1:height
   for j=1:width
       r(I_gray(i,j)+1)= r(I_gray(i,j)+1)+1;
    end
end  %计算灰度直方图中的数值：每个灰度级对应的像素数目。
subplot(3,3,6);stem(r);
title('计算所得灰度图像直方图');

s=zeros(1,256);
s(1)=r(1);
for i=2:256
    s(i)=s(i-1)+r(i);
end         %累积分布函数：对应的也是像素的数目。
subplot(3,3,9);stem(s);

for i=1:256
    s(i)=floor(255*s(i)/(height*width));
end   % s(i)/(height*width) 为频率，*256 为归一到0—255之间，floor为取整(整数部分)函数。【round为四舍五入函数,ceil为取整数部分加1】



 I_HE=I_gray;
for i=1:height
   for j=1:width
       I_HE(i,j)= s(I_gray(i,j)+1);
    end
end%得到均衡化后的图像。s(1)~s(256)里的数值即为灰度值，1~256标号对应的是原始灰度图像的0~255的灰度值。

m=zeros(1,256);
for i=1:height
   for j=1:width
       m(I_HE(i,j)+1)= m(I_HE(i,j)+1)+1;
    end
end  %计算直方图中的数值：每个灰度级对应的像素数目。
subplot(3,3,9);stem(m);
title('计算所得均衡化后图像直方图');



imwrite(I_gray,'1gray.png');
imwrite(I_HE,'1he.png'); 
subplot(3,3,7);imshow(I_HE);                          
title('均衡化后的图像');
subplot(3,3,8);imhist(I_HE);
title('均衡化后图像直方图');

---

结果：

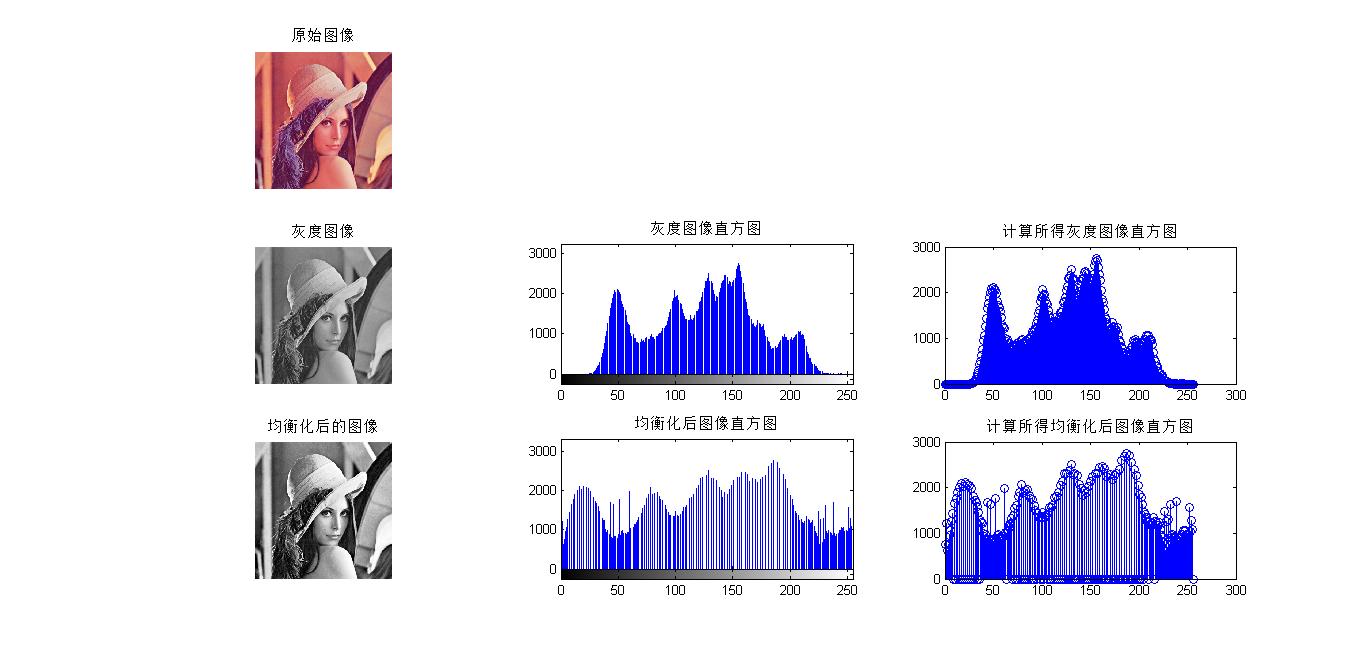
问题

直方图确实拉伸了，人眼视觉上对比度也提升了，可是说好的均匀分布呢？