你必须要了解的几种排序方法
作为一个程序员,你怎么能不了解冒泡算法呢?
下面向大家介绍六中排序算法,并提供javascript实现,以及简单分析算法复杂度。
1. 简单排序方法
1.1 冒泡排序
总体描述:
相邻元素进行比较,每次选取最大的元素,进行下一次比较,因此可以将最大的元素像冒泡一样,从某一位置,到达最顶端
算法简单描述:
假设:共有n个元素
进行(n-1)次循环,第i(从1开始计数)次循环获得第i大的元素,放在数组第(n-i)(数组从0开始计数)位
每次循环都从第一个元素开始,比较当前元素与其后一个元素的大小关系,如果后一个元素小于当前元素,则说明,当前元素较大,互换位置,即将(0~n-i区间最大的数放在n-i位),并将当前元素指向下一个位置,直到当前位置指向0,循环结束
完整代码:
function bubbleSort(originArr) { /* 数组副本 */ var cloneArr = originArr.concat(); /* 用于交换数据 */ var temp; /* 数组长度 */ var len = cloneArr.length; /* 每次选择出最大的元素 */ /* 通过比较相邻元素,将较大的元素放在后面,将较大的数继续进行比较 */ for (var i = 0; i < len - 1; ++i) { // 需要执行len-1次 for (var j = 0; j < len - i; ++j) { // 需要执行len-i-1次 // 如果当前元素大于下一个元素,互换两个元素 if (cloneArr[j] > cloneArr[j + 1]) { // 执行(1 + 2 + ... + n-1)算法复杂度为O(n^2) temp = cloneArr[j]; cloneArr[j] = cloneArr[j + 1]; cloneArr[j + 1] = temp; } } } return cloneArr; }
1.2 选择排序
总体描述:
每次选择最小的元素,放在相应的位置上
算法简单描述:
假设:共有n个元素
进行(n-1)次循环,第i(从1开始计数)次循环获得第i小的元素,放在数组第(i-1)(数组从0开始计数)位,第i次循环,从数组第(i-1)位开始,将该位置元素与其后所有元素进行比较,获取较小元素索引,循环结束之后,将当前元素与最小索引位置元素位置互换,当前位置向前移动,进行下一轮循环,直到当前位置指向(n-1)
完整代码:
function selectionSort(originArr) { /* 数组副本 */ var cloneArr = originArr.concat(); /* 用于交换数据 */ var temp; /* 存放最小元素索引 */ var minIndex = 0; /* 数组长度 */ var len = cloneArr.length; /* 从第一个位置开始,比较当前位置和后面所有元素,获取最小元素后面的位置 */ for (var i = 0; i < len - 1; ++i) { // 需要执行len-1次 minIndex = i; // 获取最小元素位置 for (var j = i + 1; j < len; ++j) { // 需要执行len-i-1次 if (cloneArr[minIndex] > cloneArr[j]) { // 执行(1 + 2 + ... + n-1)算法复杂度为O(n^2) minIndex = j; } } // 如果最小元素所在索引,不是当前位置,交换元素 if (minIndex !== i) { temp = cloneArr[i]; cloneArr[i] = cloneArr[minIndex]; cloneArr[minIndex] = temp; } } return cloneArr; }
1.3 插入排序
总体描述:
将数组分为前后两部分,前一部分是已排序的元素集合,后一部分是未排序的元素集合。每次选中未排序的第一个数组,插入到已排序集合中的合适的位置
算法简单描述:
假设:共有n个元素
从第2个元素开始,进行(n-1)次循环,第i次循环,将第i个元素插入到之前位置(1~i-1)中,将当前元素依次后面元素进行比较。比较元素起始值为当前元素前一位置元素,如果当前元素小于比较元素,比较元素向数组后面移动,当前元素继续与下一个元素进行比较,直到比较元素位置为0或者当前元素大于比较元素,将元素插入当前比较位置
完整代码:
function insertSort(originArr) { /* 数组副本 */ var cloneArr = originArr.concat(); /* 用于交换数据 */ var temp; /* 数组长度 */ var len = cloneArr.length; /* 循环数组中的每一个元素 */ for (var i = 1; i < len; ++i) { // 需要执行len-1次 // 记录要插入的值 temp = cloneArr[i]; // 找到合适的位置插入 for (var j = i - 1; j >= 0; --j) { // 需要执行i次 if (temp < cloneArr[j]) { // 执行(1 + 2 + ... + n-1)算法复杂度为O(n^2) // 右移已排序数组 cloneArr[j + 1] = cloneArr[j]; } else { break; } } cloneArr[j + 1] = temp; } return cloneArr; }
2. 高级排序算法
2.1 希尔排序
总体描述:
希尔排序就是插入排序的优化,插入排序,每次将当前元素与之前的每一个元素进行比较,然后插入,希尔排序,相当于先按照一定步长,将数组进行分组,对每一组进行插入排序,这样就可以大幅度的调整数据的分布情况,最后执行一次快速排序进行微调
算法简单描述:
对于间隔数组中的每个元素gap,将数组元素根据gap分为gap组,对于每组进行插入排序
完整代码:
function shellSort(originArr) { /* 数组副本 */ var cloneArr = originArr.concat(); /* 用于交换数据 */ var temp; /* 数组长度 */ var len = cloneArr.length; /* 间隔数组 */ var gap = []; /* 动态创建间隔数组 */ for (var i = Math.floor(len / 2); i > 0;) { gap.push(i); i = Math.floor(i / 2); } /* 使用间隔数组中的每一个元素,选择数组中的元素,进行快速排序 */ /* 方法1: 对每一个间隔的每一个分组进行快速排序 */ /*for (var i = 0, gapLen = gap.length; i < gapLen; ++i) { // 分为gap[i]组分别进行排序 for (var j = 0; j < gap[i]; ++j) { // 第j组进行排序 for (var k = j + gap[i]; k < len; k = k + gap[i]) { temp = cloneArr[k]; while (k - gap[i] >= 0 && cloneArr[k - gap[i]] > temp) { cloneArr[k] = cloneArr[k - gap[i]]; k = k - gap[i]; } cloneArr[k] = temp; } } }*/ /* 方法2: 对于每一个间隔,从间隔位置开始,对其后每一个元素进行快速排序,保证前面的已经排好序 */ for (var i = 0, gapLen = gap.length; i < gapLen; ++i) { for (var j = gap[i]; j < len; ++j) { temp = cloneArr[j]; var k = j; while (k - gap[i] >= 0 && cloneArr[k - gap[i]] > temp) { cloneArr[k] = cloneArr[k - gap[i]]; k -= gap[i]; } cloneArr[k] = temp; }
// 最坏情况O(n(logn)^2) 平均情况O(n(logn)^2) } return cloneArr; }
2.2 快速排序
总体描述:
每次选取一个基准值,将数组中其他的元素和它进行比较,大于则移到数组右边,小于则移到左边。然后分类出来的数组继续进行上述操作。
算法简单描述:
选择数组第一位元素位基准值,创建两个新数组,分别存放小于基准值和大于基准值的元素。然后这两个新数组递归进行上述操作,直到数组为空。然后将左右数组和基准值进行拼接
完整代码:
function quickSort(originArr) { /* 如果数组为空,直接返回 */ if (originArr.length === 0) { return []; } /* 基准值 */ var pivot = originArr[0]; /* 分别存放大于小于数组 */ var lesser = []; var greater = []; /* 小于基准值,存放到lesser数组中,否则存放到greater数组中 */ for (var i = 1; i < originArr.length; ++i) { if (originArr[i] < pivot) { lesser.push(originArr[i]); } else { greater.push(originArr[i]); }
// 最坏情况O(n^2) 平均情况O(nlogn) } /* 将数组拼接后返回 */ return quickSort(lesser).concat(pivot, quickSort(greater)); }
2.3 归并排序
总体描述:
自顶向下:先通过递归分解数组,再合并数组
算法简单描述:
分解数组:如果数组长度不为1,从中间将数组分为两部分,继续分解
合并数组:将分解的数组融合,创建一个新数组,用于存放融合的数组元素。创建指针分别指向两个数组的首位,比较当前指针指向位置元素的大小,将较小的元素插入新数组中,指针向后移动,直到有一个数组元素全部移出。最后检查两个数组,将未移出的元素追加到新数组中,最后存放已排序的数组根据对应位置存入待排序数组中
完整代码:
function mergeSort(originArr) { /* 数组副本 */ var cloneArr = originArr.concat(); /* 调用归并排序 */ doMergeSort(cloneArr, 0, cloneArr.length - 1); return cloneArr; } /* 向下分解数组,递归调用 */ function doMergeSort(arr, low, high) { if (low < high) { var mid = low + Math.floor((high - low) / 2); doMergeSort(arr, low, mid); doMergeSort(arr, mid + 1, high); merge(arr, low, mid, high);
// 最坏情况O(nlogn) 平均情况O(nlogn) } } /* 数组融合 */ function merge(arr, low, mid, high) { var p_low = low; var p_high = mid + 1; var sortArr = []; /* 比较左右部分元素,将较小的元素存放在sortArr前面 */ while (p_low <= mid && p_high <= high) { if (arr[p_low] > arr[p_high]) { sortArr.push(arr[p_high++]); } else { sortArr.push(arr[p_low++]); } } /* 将两部分可能剩余的元素复制到数组中 */ while (p_high <= high) { sortArr.push(arr[p_high++]); } while (p_low <= mid) { sortArr.push(arr[p_low++]); } /* 将已排序的数组复制到原数组对应位置 */ for (var i = low; i < high + 1; i++) { arr[i] = sortArr[i - low]; } }
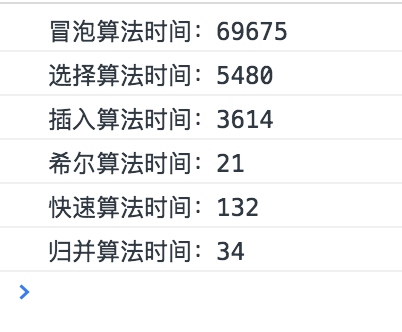
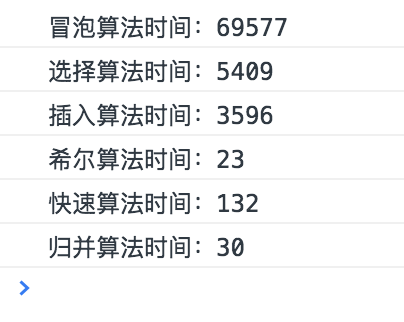
3. 最终测试结果
100000数组测试:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号