树链剖分算法详解
学OI也有一段时间了,感觉该搞点东西了。
于是学习了树(熟)链(练)剖(pou)分(粪)
当然,学习这个算法是需要先学习线段树的。不懂的还是再过一段时间吧。
如果碰到一道题,要对一颗树的两个点中的最短路径、以u为根的子树之类的东西进行修改或者查询,那么大概就是树链剖分的题了。
树链剖分就是把一颗树的节点按照新的顺序扔到一颗线段树里面,然后保证一条树链上的点在线段树中尽可能连续。
为什么是尽可能?因为在一棵树中,怎么搞也无法保证对于每一个节点,他的父亲编号都是它的-1,所以是尽可能。那么怎么尽可能呢?
有很多算法,今天提到的就是树链剖分。我们把一颗树上的所有链分成轻链和重链,然后就可以对于每一段连续的重链进行线段树上的修改了。
而划分轻链和重链的依据是:对于每一个节点u,v是它的儿子,v有一个大小,就是size,代表以v为根的子树的大小。我们选取u最大的儿子为重(zhong)儿子,其余儿子为轻儿子。以连向重儿子的边为重边,剩下的边为轻边。
然后所有重边连成的链叫做重链,(并不存在轻链)比如下图,红色的链是重链(注意,对于一个叶子节点,如果连向它的是一条轻链,那么他自己就是一条重链)
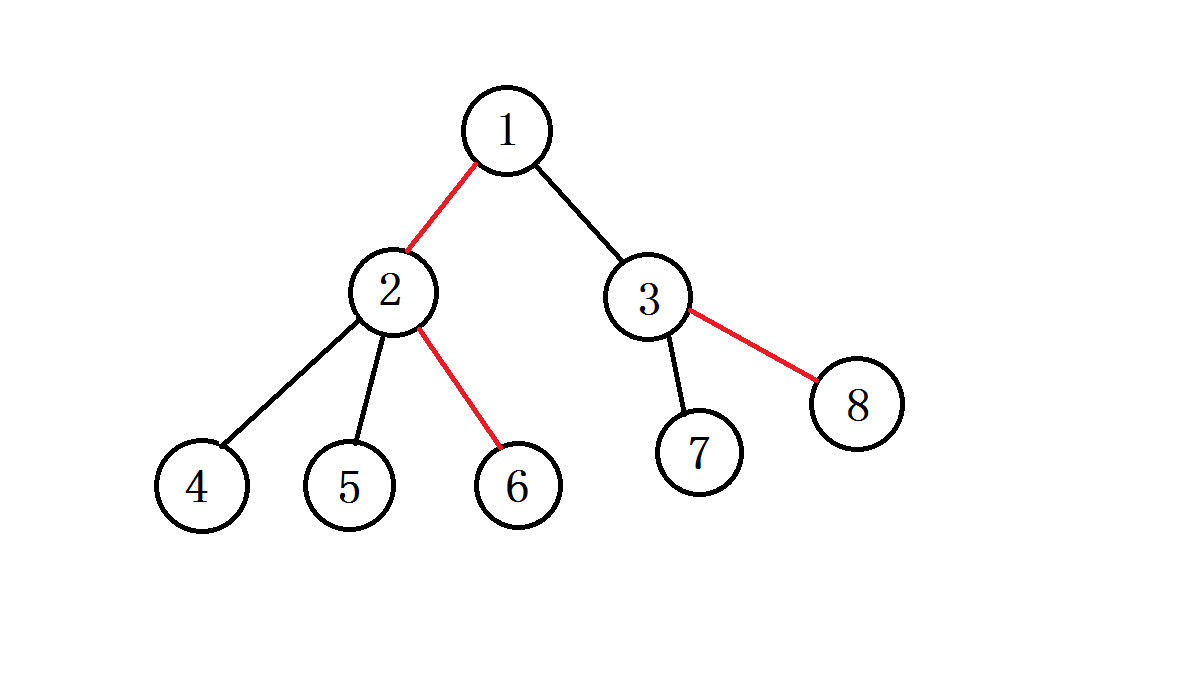
这样,我们把一棵树划分成了重链和轻链,我们能保证所有重链都不重不漏的包含了所有的点。
那么这些重链有什么用?在划分重链的过程中用到的DFS,这个DFS能保证,对于每一条重链,他们的DFS序是连续的!
这样,我们就可以用线段树(或者其他数据结构)维护了!
现在,我们把熟练剖分化成两个部分:
1、把树上的所有点划分重链,然后求出它们的DFS序,以这个顺序扔到线段树里面。
2、在线段树上进行维护。
所以,如何实现划分重链?我们需要用两个DFS,第一个DFS找到所有点的重儿子,第二个DFS将所有重儿子连成重链。
第一个DFS:size是以当前点为根的子树的大小,f是当前点的父亲,son是当前点的重儿子。
inline void getson(int u,int fa){//获取每个节点的重儿子 size[u]=1; for(int e=head[u];e;e=nxt[e]) if(to[e]!=fa){ depth[to[e]]=depth[u]+1; f[to[e]]=u; getson(to[e],u); size[u]+=size[to[e]];//记录以每个节点为根的树的大小 if(!son[u] || size[son[u]]<size[to[e]]) son[u]=to[e];//判断后将这个点变为重儿子 } return ; }
第二个DFS:
inline void getdfn(int u,int t){//连成重链,其中我们可以保证,对于每一条重链,它们的dfn值是连续的。t记录的是当前链的链首 top[u]=t;//top记录当前链链首 dfn[u]=++cnt;//记录dfn值,也是在线段树中的位置 link[cnt]=u;//dfn的逆运算,用于建树时的初始赋值 if(!son[u]) return ;//如果当前点没有重儿子,说明是这条重链的结束。 getdfn(son[u],t);//继续走这条重链 for(int e=head[u];e;e=nxt[e])//这个相当于走每一条轻链 if(to[e]!=son[u] && to[e]!=f[u]) getdfn(to[e],to[e]);//重新开始走每一条重链 return ; }
然后,对于线段树的建树,是独立的,我们不用考虑链的关系。(input是输入文件)
inline void build(int i,int l,int r){//平凡的建树 tree[i].l=l,tree[i].r=r; if(l==r){ tree[i].sum=input[link[l]]%mod;//link的作用 return ; } int mid=(l+r)>>1; build(i<<1,l,mid); build(i<<1|1,mid+1,r); tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%mod; return ; }
最后是修改,查询和修改很像,一起说了。
我们要把u到v路径上所有的点都+k,那么我们就把u,v中深的那个,它到它所在重边的顶端+k。
然后跳过一条轻边,重复上面的步骤,知道u,v到一条重边上。
最后把u到v,+k就可以了。
inline void treeadd(int x,int y,int z){//将题中对树的修改转化成对线段树的修改 int tx=top[x],ty=top[y]; while(tx!=ty){//如果两个点不在一条重链上 if(depth[tx]<depth[ty]) swap(x,y),swap(tx,ty);//保证x的重链首元素在下方 add(1,dfn[tx],dfn[x],z);//从x一直修改到x所在重链的收元素,因为他们在一条重链中,所以在线段树中的位置是连续的。 x=f[tx];//走过一条轻链,到上面一个重链的末尾 tx=top[x],ty=top[y];//分别更新x、y的重链顶端,准备下一次更新 } if(depth[x]<depth[y]) swap(x,y);//现在x、y都到了一条重链上了,然后要保证x在下面。 add(1,dfn[y],dfn[x],z);//再只用更新他们所在的链就可以了。 return ; } inline int treesum(int x,int y){//将题中对树查询得指令改为对线段树的查询。 int ans=0; int tx=top[x],ty=top[y]; while(tx!=ty){//这一段和修改几乎一样,就是把原本对每一个区间的修改,变为了查询,其实都一样。 if(depth[tx]<depth[ty]) swap(tx,ty),swap(x,y); ans=(ans+query(1,dfn[tx],dfn[x]))%mod; x=f[tx]; tx=top[x],ty=top[ty]; } if(depth[x]<depth[y]) swap(x,y); return (ans+query(1,dfn[y],dfn[x]))%mod; }
对于线段树上的维护,和朴素的线段树一样,就不多说了。
如果题目中说要将以i为根的子树+k,那就直接在线段树上从dfn[i]到dfn[i]+size[i],+k就可以了。
具体看AC代码:(洛谷模板题)
#include <iostream> #include <cstdio> #include <algorithm> #include <cstdlib> #include <cstring> #define in(a) a=read() #define REP(i,k,n) for(int i=k;i<=n;i++) #define MAXN 100010 using namespace std; inline int read(){ int x=0,f=1; char ch=getchar(); for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1; for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0'; return x*f; } int n,m,r,mod,input[MAXN]; int total,head[MAXN],to[MAXN<<1],nxt[MAXN<<1]; int size[MAXN],depth[MAXN],f[MAXN],son[MAXN]; int cnt,dfn[MAXN],link[MAXN],top[MAXN]; struct node{ int l,r,sum,lt; }tree[MAXN<<2]; inline void adl(int a,int b){ total++; to[total]=b; nxt[total]=head[a]; head[a]=total; return ; } inline void getson(int u,int fa){//获取每个节点的重儿子 size[u]=1; for(int e=head[u];e;e=nxt[e]) if(to[e]!=fa){ depth[to[e]]=depth[u]+1; f[to[e]]=u; getson(to[e],u); size[u]+=size[to[e]];//记录以每个节点为根的树的大小 if(!son[u] || size[son[u]]<size[to[e]]) son[u]=to[e];//判断后将这个点变为重儿子 } return ; } inline void getdfn(int u,int t){//连成重链,其中我们可以保证,对于每一条重链,它们的dfn值是连续的。t记录的是当前链的链首 top[u]=t;//top记录当前链链首 dfn[u]=++cnt;//记录dfn值,也是在线段树中的位置 link[cnt]=u;//dfn的逆运算,用于建树时的初始赋值 if(!son[u]) return ;//如果当前点没有重儿子,说明是这条重链的结束。 getdfn(son[u],t);//继续走这条重链 for(int e=head[u];e;e=nxt[e])//这个相当于走每一条轻链 if(to[e]!=son[u] && to[e]!=f[u]) getdfn(to[e],to[e]);//重新开始走每一条重链 return ; } inline void build(int i,int l,int r){//平凡的建树 tree[i].l=l,tree[i].r=r; if(l==r){ tree[i].sum=input[link[l]]%mod;//link的作用 return ; } int mid=(l+r)>>1; build(i<<1,l,mid); build(i<<1|1,mid+1,r); tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%mod; return ; } inline void pushdown(int i){//平凡的pushdown if(!tree[i].lt) return ; tree[i<<1].lt+=tree[i].lt; tree[i<<1|1].lt+=tree[i].lt; int mid=(tree[i].l+tree[i].r)>>1; tree[i<<1].sum=(tree[i<<1].sum+(mid-tree[i].l+1)*tree[i].lt)%mod; tree[i<<1|1].sum=(tree[i<<1|1].sum+(tree[i].r-mid)*tree[i].lt)%mod; tree[i].lt=0; return ; } inline void add(int i,int l,int r,int k){//平凡的区间修改 if(tree[i].l>=l && tree[i].r<=r){ tree[i].sum=(tree[i].sum+(tree[i].r-tree[i].l+1)*k)%mod; tree[i].lt+=k; return ; } pushdown(i); if(tree[i<<1].r>=l) add(i<<1,l,r,k); if(tree[i<<1|1].l<=r) add(i<<1|1,l,r,k); tree[i].sum=(tree[i<<1].sum+tree[i<<1|1].sum)%mod; return ; } inline int query(int i,int l,int r){//平凡的区间查询 if(tree[i].l>=l && tree[i].r<=r) return tree[i].sum; int sum=0; pushdown(i); if(tree[i<<1].r>=l) sum=(sum+query(i<<1,l,r))%mod; if(tree[i<<1|1].l<=r) sum=(sum+query(i<<1|1,l,r))%mod; return sum; } inline void treeadd(int x,int y,int z){//将题中对树的修改转化成对线段树的修改 int tx=top[x],ty=top[y]; while(tx!=ty){//如果两个点不在一条重链上 if(depth[tx]<depth[ty]) swap(x,y),swap(tx,ty);//保证x的重链首元素在下方 add(1,dfn[tx],dfn[x],z);//从x一直修改到x所在重链的收元素,因为他们在一条重链中,所以在线段树中的位置是连续的。 x=f[tx];//走过一条轻链,到上面一个重链的末尾 tx=top[x],ty=top[y];//分别更新x、y的重链顶端,准备下一次更新 } if(depth[x]<depth[y]) swap(x,y);//现在x、y都到了一条重链上了,然后要保证x在下面。 add(1,dfn[y],dfn[x],z);//再只用更新他们所在的链就可以了。 return ; } inline int treesum(int x,int y){//将题中对树查询得指令改为对线段树的查询。 int ans=0; int tx=top[x],ty=top[y]; while(tx!=ty){//这一段和修改几乎一样,就是把原本对每一个区间的修改,变为了查询,其实都一样。 if(depth[tx]<depth[ty]) swap(tx,ty),swap(x,y); ans=(ans+query(1,dfn[tx],dfn[x]))%mod; x=f[tx]; tx=top[x],ty=top[ty]; } if(depth[x]<depth[y]) swap(x,y); return (ans+query(1,dfn[y],dfn[x]))%mod; } int main(){ in(n),in(m),in(r),in(mod); REP(i,1,n) in(input[i]); int a,b; REP(i,1,n-1) in(a),in(b),adl(a,b),adl(b,a); depth[r]; getson(r,0); getdfn(r,r); build(1,1,n); int p,x,y,z; REP(i,1,m){ in(p); if(p==1) in(x),in(y),in(z),treeadd(x,y,z); if(p==2) in(x),in(y),printf("%d\n",treesum(x,y)); if(p==3) in(x),in(z),add(1,dfn[x],dfn[x]+size[x]-1,z);//我们会发现,在树链剖分中,i这颗子树里面所有的节点的dfn都是连续的,我们修改u的子树就是将u到u+size-1修改就可以了。 if(p==4) in(x),printf("%d\n",query(1,dfn[x],dfn[x]+size[x]-1));//查询同上。 } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号