noip2013 车站分级

题目描述

一条单向的铁路线上，依次有编号为 1, 2, …, n1,2,…,n的 nn个火车站。每个火车站都有一个级别，最低为 11 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 xx，则始发站、终点站之间所有级别大于等于火车站xx 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

例如，下表是55趟车次的运行情况。其中，前44 趟车次均满足要求，而第 55 趟车次由于停靠了 33 号火车站（22 级）却未停靠途经的 66 号火车站（亦为 22 级）而不满足要求。

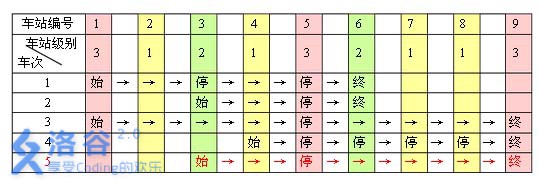
现有 mm 趟车次的运行情况（全部满足要求），试推算这nn 个火车站至少分为几个不同的级别。

输入输出格式

输入格式：

 

第一行包含 22 个正整数 n, mn,m，用一个空格隔开。

第 i + 1i+1 行(1 ≤ i ≤ m)(1≤i≤m)中，首先是一个正整数 s_i(2 ≤ s_i ≤ n)si​(2≤si​≤n)，表示第ii 趟车次有 s_isi​ 个停靠站；接下来有s_isi​个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

 

输出格式：

 

一个正整数，即 nn 个火车站最少划分的级别数。

 

一开始，写了一个差分约束，跑了个最长路，结果建边写挂了。

后来就写了一个topo排序，重点在连边。

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <cstdlib>
#include <algorithm>
#define REP(i,k,n) for(int i=k;i<=n;i++)
#define in(a) a=read()
#define MAXN 1010
using namespace std;
typedef pair<int,int> P;
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar())
        if(ch=='-')
            f=-1;
    for(;isdigit(ch);ch=getchar())
        x=x*10+ch-'0';
    return f*x;
}
struct node{
    int a,b;
};
int n,m,s,x,t;
int total=0,head[MAXN],nxt[MAXN<<10],to[MAXN<<10],val[MAXN<<10];
int du[MAXN],ans;
int a[MAXN],is[MAXN];
int dis[MAXN],vis[MAXN];
int book[MAXN][MAXN];
queue <int> Q;
inline void adl(int a,int b){
    total++;
    du[b]++;
    to[total]=b;
    nxt[total]=head[a];
    head[a]=total;
    return ;
}
inline void topo(){
    while(!Q.empty()){
        int u=Q.front();
        Q.pop();
        for(int e=head[u];e;e=nxt[e]){
            du[to[e]]--;
            dis[to[e]]=dis[u]+1;
            ans=max(ans,dis[to[e]]);
            if(!du[to[e]])
                Q.push(to[e]);
        }
    }
    return ;
}
int main(){
    in(n);in(m);
    REP(i,1,m){
        memset(a,0,sizeof(a));
        memset(is,0,sizeof(is));
         in(s),t=0;
         REP(j,1,s)
           in(a[j]),is[a[j]]=1;
         REP(j,a[1]+1,a[s]){
             if(is[j])  continue;
             REP(k,1,s)
                 if(!book[j][a[k]]){
                     book[j][a[k]]=1;
                     adl(j,a[k]);
                 }
         }
    }
    REP(i,1,n)
        if(!du[i])
            vis[i]=1,dis[i]=1,Q.push(i);
    topo();
    cout<<ans;
    return 0;
}