区间DP

1、石子合并

题目描述

在一个圆形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出1个算法,计算出将N堆石子合并成1堆的最小得分和最大得分.

输入输出格式

输入格式：

 

数据的第1行试正整数N,1≤N≤100,表示有N堆石子.第2行有N个数,分别表示每堆石子的个数.

 

输出格式：

 

输出共2行,第1行为最小得分,第2行为最大得分.

 

输入输出样例

输入样例#1： 

4
4 5 9 4

输出样例#1： 

43
54

DP转移方程：

f1[i][j]=max(f1[i][j],f1[i][k]+f1[k+1][j]+sum[j]-sum[i-1]);
f2[i][j]=max(f2[i][j],f2[i][k]+f[k+1][j]+sum[j]-sum[i-1]);

2、能量项链

题目描述

在 MarsMars 星球上，每个 MarsMars 人都随身佩带着一串能量项链。在项链上有 NN 颗能量珠。能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。因为只有这样，通过吸盘（吸盘是 MarsMars 人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为 mm ，尾标记为 rr ，后一颗能量珠的头标记为r，尾标记为 nn ，则聚合后释放的能量为 m \times r \times nm×r×n （ MarsMars 单位），新产生的珠子的头标记为 mm，尾标记为 nn 。

需要时， MarsMars 人就用吸盘夹住相邻的两颗珠子，通过聚合得到能量，直到项链上只剩下一颗珠子为止。显然，不同的聚合顺序得到的总能量是不同的，请你设计一个聚合顺序，使一串项链释放出的总能量最大。

例如：设 N=4N=4 ， 44 颗珠子的头标记与尾标记依次为 (2,3) (3,5) (5,10) (10,2)(2,3)(3,5)(5,10)(10,2) 。我们用记号⊕表示两颗珠子的聚合操作，( jj ⊕ kk )表示第 j,kj,k 两颗珠子聚合后所释放的能量。则第 44 、 11 两颗珠子聚合后释放的能量为：

( 44 ⊕ 11 ) =10 \times 2 \times 3=60=10×2×3=60 。

这一串项链可以得到最优值的一个聚合顺序所释放的总能量为：

(( 44 ⊕ 11 )⊕ 22 )⊕ 33 ）= 10 \times 2 \times 3+10 \times 3 \times 5+10 \times 5 \times 10=71010×2×3+10×3×5+10×5×10=710 。

输入输出格式

输入格式：

 

第一行是一个正整数 N(4≤N≤100)N(4≤N≤100) ，表示项链上珠子的个数。第二行是 NN 个用空格隔开的正整数，所有的数均不超过 10001000 。第 ii 个数为第 ii 颗珠子的头标记 (1≤i≤N)(1≤i≤N) ，当 i<N< span>i<N<span> 时，第 ii 颗珠子的尾标记应该等于第 i+1i+1 颗珠子的头标记。第 NN 颗珠子的尾标记应该等于第 11 颗珠子的头标记。

至于珠子的顺序，你可以这样确定：将项链放到桌面上，不要出现交叉，随意指定第一颗珠子，然后按顺时针方向确定其他珠子的顺序。

 

输出格式：

 

一个正整数 E(E≤2.1 \times (10)^9)E(E≤2.1×(10)9) ，为一个最优聚合顺序所释放的总能量。

 

输入输出样例

输入样例#1： 

4
2 3 5 10

输出样例#1： 

710

DP转移方程：f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]+m[i]*t[k]*m[j]);

题目描述：

用多边形顶点的逆时针序列表示凸多边形，即P={v0,v1,…,vn-1}表示具有n条边的凸多边形。

     

　　给定凸多边形P，以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分，使得即该三角剖分中诸三角形上权之和为最小。

 

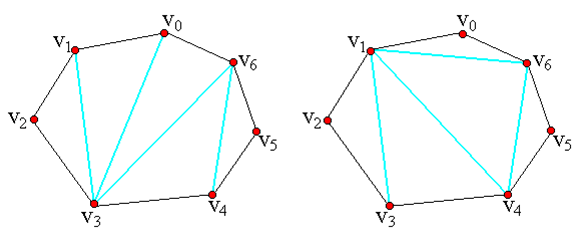
DP转移方程：f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+a[i]*a[j]*a[k]);

 

题目描述：

描述给你一个字符串，里面只包含"(",")","[","]"四种符号，请问你需要至少添加多少个括号才能使这些括号匹配起来。
如：
[]是匹配的
([])[]是匹配的
((]是不匹配的
([)]是不匹配的

 

输入：

第一行输入一个正整数N，表示测试数据组数(N<=10)
每组测试数据都只有一行，是一个字符串S，S中只包含以上所说的四种字符，S的长度不超过100

输出：

对于每组测试数据都输出一个正整数，表示最少需要添加的括号的数量。每组测试输出占一行

样例输入：

4
[]
([])[]
((]
([)]

样例输出：

0
0
3
2

DP转移方程：

f[i][i]=1;
if(s[i]==s[j] && j!=i+1)
f[i][j]=min(f[i][j],f[i+1][j-1]);
f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]);

 

题目描述

帅帅经常跟同学玩一个矩阵取数游戏：对于一个给定的n×mn×m的矩阵，矩阵中的每个元素aijaij均为非负整数。游戏规则如下：

1.每次取数时须从每行各取走一个元素，共n个。m次后取完矩阵所有元素；

2.每次取走的各个元素只能是该元素所在行的行首或行尾；

3.每次取数都有一个得分值，为每行取数的得分之和，每行取数的得分=被取走的元素值×2i每行取数的得分=被取走的元素值×2i，其中i表示第i次取数（从1开始编号）；

4.游戏结束总得分为m次取数得分之和。

帅帅想请你帮忙写一个程序，对于任意矩阵，可以求出取数后的最大得分。

输入输出格式

输入格式：

 

输入文件game.in包括n+1行：

第1行为两个用空格隔开的整数n和m。

第2~n+1行为n*m矩阵，其中每行有m个用单个空格隔开的非负整数。

数据范围：

60%的数据满足：1<=n, m<=30，答案不超过10^16

100%的数据满足：1<=n, m<=80，0<=aijaij<=1000

 

输出格式：

 

输出文件game.out仅包含1行，为一个整数，即输入矩阵取数后的最大得分。

 

输入输出样例

输入样例#1：

2 3
1 2 3
3 4 2

输出样例#1：

82

DP转移方程：

矩阵取数游戏
f[i][i]=a[i]*2^m;
f[i][j]=max(f[i][j],f[i+1][j]+a[i]*2^k,f[i][j-1]+a[m-j-i]*2^k);