Tarjan 算法详解
一个神奇的算法,求最大连通分量用O(n)的时间复杂度,真实令人不可思议。
废话少说,先上题目
题目描述:
给出一个有向图G,求G连通分量的个数和最大连通分量。
输入:
n,m,表示G有n个点,m条边
下面m行每行包含 x,y,表示有一条x到y的有向边
输出:
第一个数表示连通分量的个数,第二个数代表最大连通分量
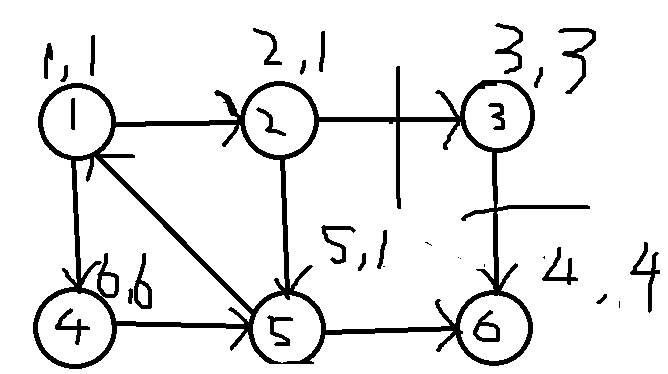
输入示例(如下图)
6 8 1 2 1 4 2 3 2 5 3 6 4 5 5 1 5 6
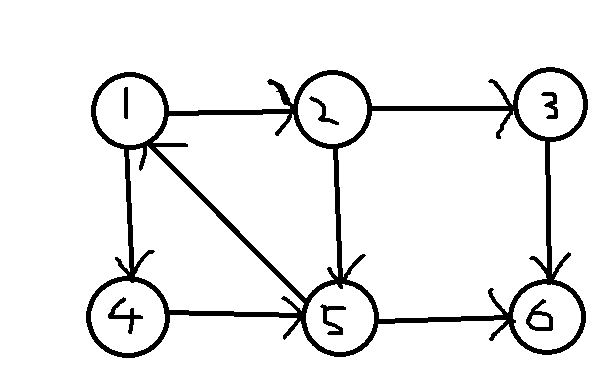
输入示例
4 3
很多人会想到DFS,但是时间复杂度为O(n^2),但是时间容易超限,所以我们要用到Tarjan
先理清一下概念:
连通分量:对于图G来的一个子图中,任意两个点都可以彼此到达,这个子图就被称为图G的连通分量(一个点就是最小的连通分量)
最大连通分量:对于图G的一个子图,这个子图为图G的连通分量,且是图G所有连通分量中包含节点数最多的那个,即为G的最大联通分量
时间戳:搜索时第几个搜索到这个点。如搜索顺序是1->2->3->6则6的时间截为4
下面就是tarjan的思路(第一次看不懂可以跳过,直接看详细步骤,回来再看):
每个点都有两个参数:low,dfn。dfn表示这个点的时间戳,而low代表这个点所能到达的最小的时间戳,开始low都等于dfn,但会经过不断更新而减少。
从1节点进行深度优先搜索,途中用树(一个转化为栈的树)维护。
当遇到一个点时,有如下判断:
1、如果这个点没有访问过,就将这个点加入树(栈)
2、如果这个点访问过,且在树(栈)里,与这个点的low比较,更新自己的low
返回时更新low
当一个点遍历所有的边后这个点的low还是等于dfn,将个点及以上出栈,这个点及栈以上的点构成一个连通分量。
来一点Chinese++(就是伪代码)
void tarjan(int 当前点) { 这个点的low=dfn=时间戳; 将这个点入栈; 标记这个点入栈; 枚举这个点连接的所有边 { 如果目标点没有被访问过 { tarjan(目标点); 更新当前点的low; } 如果目标点被访问过 { 更新当前点的low; } } 如果当前点的low==dfn { 将这个点及栈以上的点出栈,标记成一个强连通分量; ans++; } }
详细过程:
开启黑暗之门

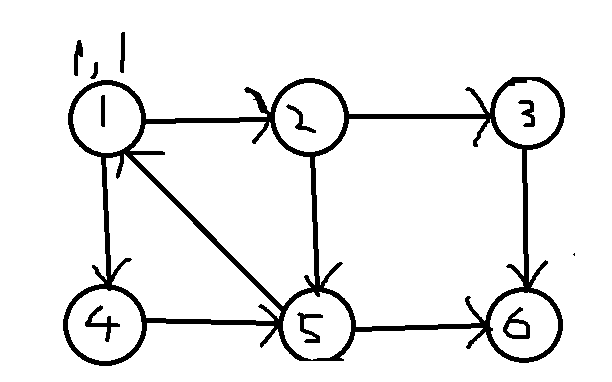
开始,从1节点开始,时间截和low都是1,将1入栈
stack:1,

走到2节点,2的时间戳dfn和low都是2,2入栈
stack:1,2
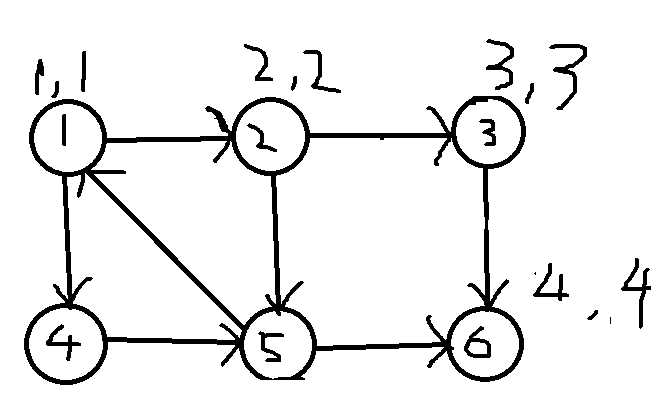
以此类推,将3、6入栈,时间戳分别为3、4
stack:1,2,3,6

此时,发现6节点遍历了其所有出边(本来就没有)以后,它的low等于dfn,这就说明了6号节点没有路径能回到能到达它的节点,所以6就是一个单独的连通分量,因此将6出栈,再回溯,此时在栈中比6(含)高的点都出栈,这些点构成一个连通分量(因为此时比6在栈顶,所以6是一个单独的连通分量)ans++
stack:1,2,3
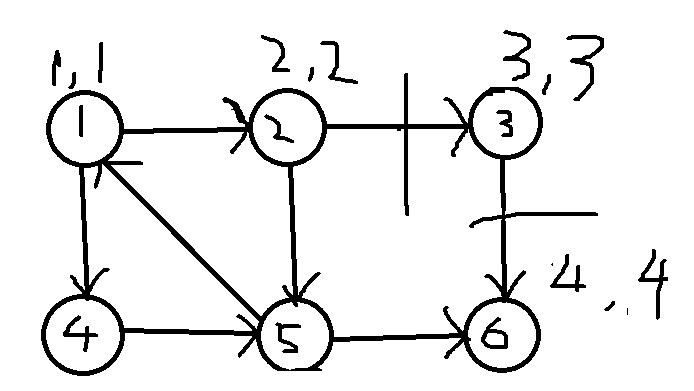
和刚才一样,3节点的所有出边已经遍历一般,但low还是和dfn相等,所以3出栈,因为此时3在栈顶,所以3是一个单独的连通分量。ans++
stack:1,2

再次遍历从2遍历到5,将5入栈,并且low和dfn都为5。
stack:1,2,5
然后5搜索到6,但是6不在栈里面,所以不管它

这是搜索到了1,发现1的时间戳1小于5的low,所以将5的low更新为1,。这时发现5没有其他边可以走了,所以返回

返回到2时,发现5的low比2的low小,所以更新2的low为1,继续返回到1
再从1走到4,4的时间戳和low为6,将4入栈
stack:1,2,5,4

从4走到5,发现5在栈中,且5的low比4的low小,所以4的low变成1,因为没有边再返回到1
此时,1的所有边都走完啦,并且1的low等于dfn,所以把1及以上的节点出栈,构成连通分量,ans++
继续枚举每一个点,如果这个点的时间戳为0(也就是没有访问过)tarjan(i);
现在贴上代码,但是没有完,我会对原理做详细解释:
void tarjan(int u) { in++; dfn[u]=in; low[u]=in; S.push(u); vis[u]=1; for(int e=head[u];e;e=next[e]) { if(!dfn[to[e]]) { tarjan(to[e]); low[u]=min(low[to[e]],low[u]); } else if(vis[to[e]]) low[u]=min(low[u],dfn[to[e]]); } if(low[u]==dfn[u]) { while(!S.empty() && S.top()!=u) { vis[S.top()]=0; S.pop(); } vis[u]=0; S.pop(); ans++; } }
演员表:
in:时间戳下标
dfn[i]:i节点的时间戳
low[i]:i所能到达的最小的时间戳
head[i],next[i],to[i]:邻接表群演
vis[i]:i是否在栈里
S:栈
ans:计数
u:当前点
原理详解:
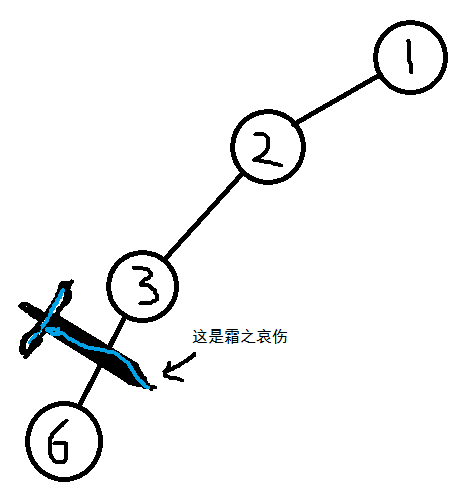
1、其实虽说整个过程都在用栈维护,但是原理却是一颗树,比如当搜索到1、2、3、6时,树是这样的

你想象成树就好,当我们确定6为一个单独的连通分量的时候,把它咔嚓掉。现在6及以下的节点(这次没有)成为一颗新的树。
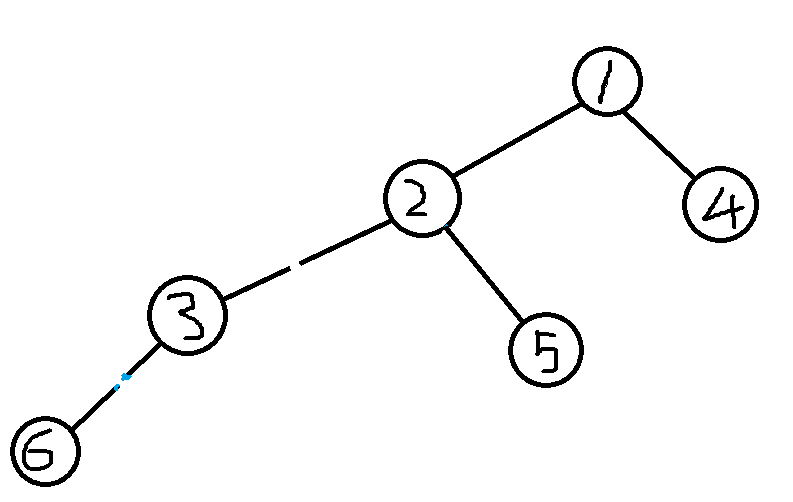
然后再用霜之哀伤砍掉3,3及以下节点(也是没有)又变成了一个新的树。
然后我们搜索到5,将5加入树

然后再从1搜索到4,加入树
然后返回到1,拔出1节点的霜之哀伤与耐奥祖融合,成为新的巫妖王。
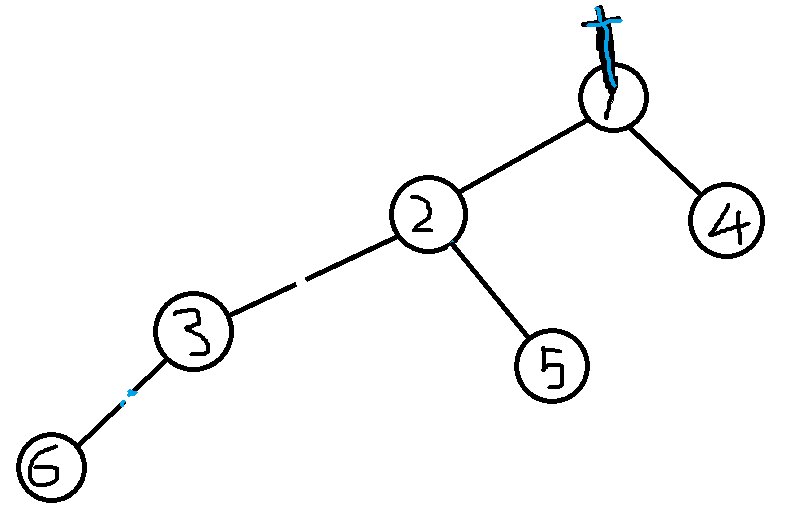

这就是Tarjan的关于连通分量个数的应用了,后续会带来割点割边。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号