线段树 入门详解

概念（copy度娘）：

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN）。而未优化的空间复杂度为2N，因此有时需要离散化让空间压缩。

通俗地讲：

线段树就是把一个线段转变为一个二叉树，如下所示：

一个线段长度为4，则把它变成线段树，就是这个样子

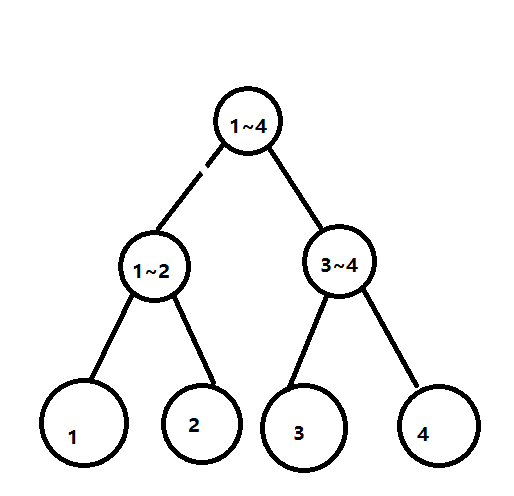
 这样如果你想改变一个区间的值，只用O（logn）。比一般算法快了许多。

但是空间复杂度就会高一些，比如本来这个线段只占4，现在变成了7.

最基本的题目：

为了方便大家了解线段树的建树+改变+查找，我就以最基本的修改区间范围值的题做示范：

题曰：给定一个长度为L的数组，每一位的开始值都是0，然后给出n条信息，每行信息包括a，b，c。

含义是在开区间（a，b）中所有的值加上c

然后输入一个k，询问k的值。

输入：

第一行输入信息数n，数组长度L。

接下来2到n+1行输入a，b，c。

最后一行输入k

输出：

k的值

输入示例：

2 4

1 3 1

2 4 4

2 

输出示例：

5

建树：

看完题后我们开始建树。

这是线段树中最简单的部分。

顺便说一下，线段树英文是：segtree

 

struct node
{
    int l,r,data;
}segtree[100010];//首先你要建一个线段树，l是这个点的左边（就比如上图根节点的1），r是这个点的右边，比如上图根节点的4。data就是这个点的增减标记，记录这个店增加了几
void build(int index,int left,int right)//递归实现建树
{
    if(left==right)//如果这个点是叶节点，就return；
    {
        segtree[index].r=right;
        segtree[index].l=left;
        return ;
    }
    segtree[index].l=left;//给此节点的左右边界赋值
    segtree[index].r=right;
    int mid=(left+right)/2;
    build(index*2,left,mid);//递归建立左子树和右子树
    build(index*2+1,mid+1,right);
} 

一上就是简单的建树，用到了递归，大家应该都能看懂。

增减值：

我实在不会术语，就这样吧。下面来教大家怎样改变线段树的值。

想要改变线段树的值，不是直接改变，因为线段树上只有一个l一个r没有表示实际的值。

这时候我们就要创建一个data，来标记这个线段树的增减。

比如我们要使2~4区间加1，可以这样

从根节点1~4区间开始搜索，发现它的左右子节点（1~2、3~4）都有2~4区间，所以搜索两边。

先搜索左子节点，发下这个节点的左节点（1~1）没有2~4，于是不搜索，接着搜索右节点（2~2），发现此节点被完全包括在了2~4，因此义不容辞地将这个点标记从原本的0加上一个1，并且断绝此节点搜索。

我们回到最开始的右节点，（3~4），发现这个节点又被完全包括在2~4里面于是标记从零到一，然后结束搜索。

一番搜索过后，线段树，也就是segtree[].data标记如下:

之后用这个来如何处理，我稍后会讲

现呈上代码（编译器坏了，手打的，难免会有一些bug，见谅）

void update(int index,int left,int right,int c)//还是递归标记
{
    if(segtree[index].l>=left && segtree[index].r<=right)//如果全都被包括，就直接加上去
   {
        segtree[index].data+=c;
        return ; 
   }
   int mid=(segtree[index].l+segtree[index].r)/2;
   if(mid>=left)//分别判断是否包含一部分
        update(index*2,left,right,c);
   if(mid<right)
       update(index*2+1,left,right,c);
}

 查询：

最激动人心的时刻到了，查询！！！其实很简单，就是从根节点一直走到你要查询的叶子节点，一路上都加上segtree[].data就好了。

上面的图，你查询3，根节点+0，往右边走+1，再往左边走+0，于是结果就是1.

代码如下：

void search(int index,int k,int ans)
{
    int left=segtree[index].l;
    int right=segtree[inrdex].r;
    if(l==k && r==k)
    {
        cout<<ans;
        return ;
    }
    int mid=(left+right)/2;
    if(k<=mid)
        search(index*2,k,ans+segtree[index].data);
    if(k>mid)
        search(index*2+1,k,ans+segtree[index].data);
}

好了，不知道完整代码还要不要，应该不要了吧。

开始build(1,1,L);

就是没读入一条信息，a，b，c然后调用update(1,a,b,c);

最后输入k调用search(1,k,0)

口胡完毕，没听懂评论就好。