bzoj4289 Tax

Description

给出一个N个点M条边的无向图，经过一个点的代价是进入和离开这个点的两条边的边权的较大值，求从起点1到点N的最小代价。起点的代价是离开起点的边的边权，终点的代价是进入终点的边的边权

N<=100000

M<=200000

Sample Input

4 5
1 2 5
1 3 2
2 3 1
2 4 4
3 4 8

Sample Output

12

 

 

很容易想到暴力：化边为点，每两个点中间的边权为两个原来边的更大的权，如图，红色的点是新点：

 

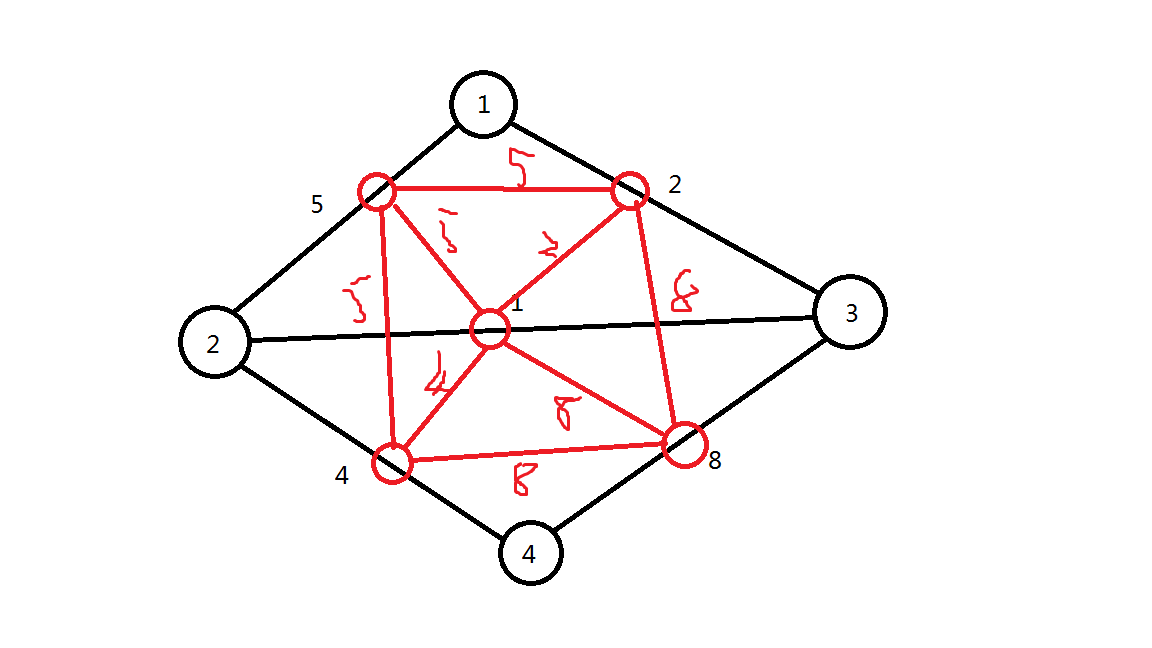
但是，如果出现了菊花图，那么新边的个数会变成M^2,原地爆炸，我们必须优化建边。

考虑把原来的无向边，变成两条有向边，也就是在新图上把一个点拆成两个点，这两个点之间的边权是原边的边权。

对于每一个原图上的点，把它的所有出边进行排序，每条出边从小到大连一条两个边权之差的边，如图：

 

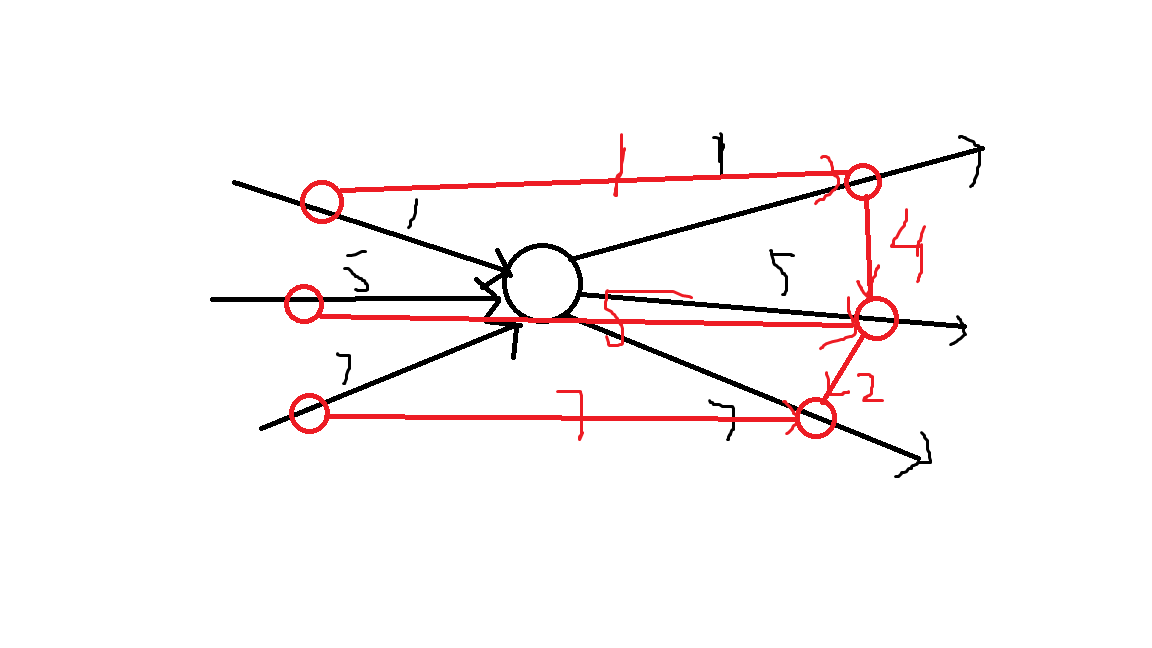
这样运用查分建图，就好比，我要过这个点，原来是一起交了钱，现在建完图是先交进入的钱，再将出边和入边的差补交上去。

然后，再将新图建立S、T分别是源点的汇点。将S连向所有原图起点的出边，所有原图终点的入边连向T。

最后图会成为这个样子：

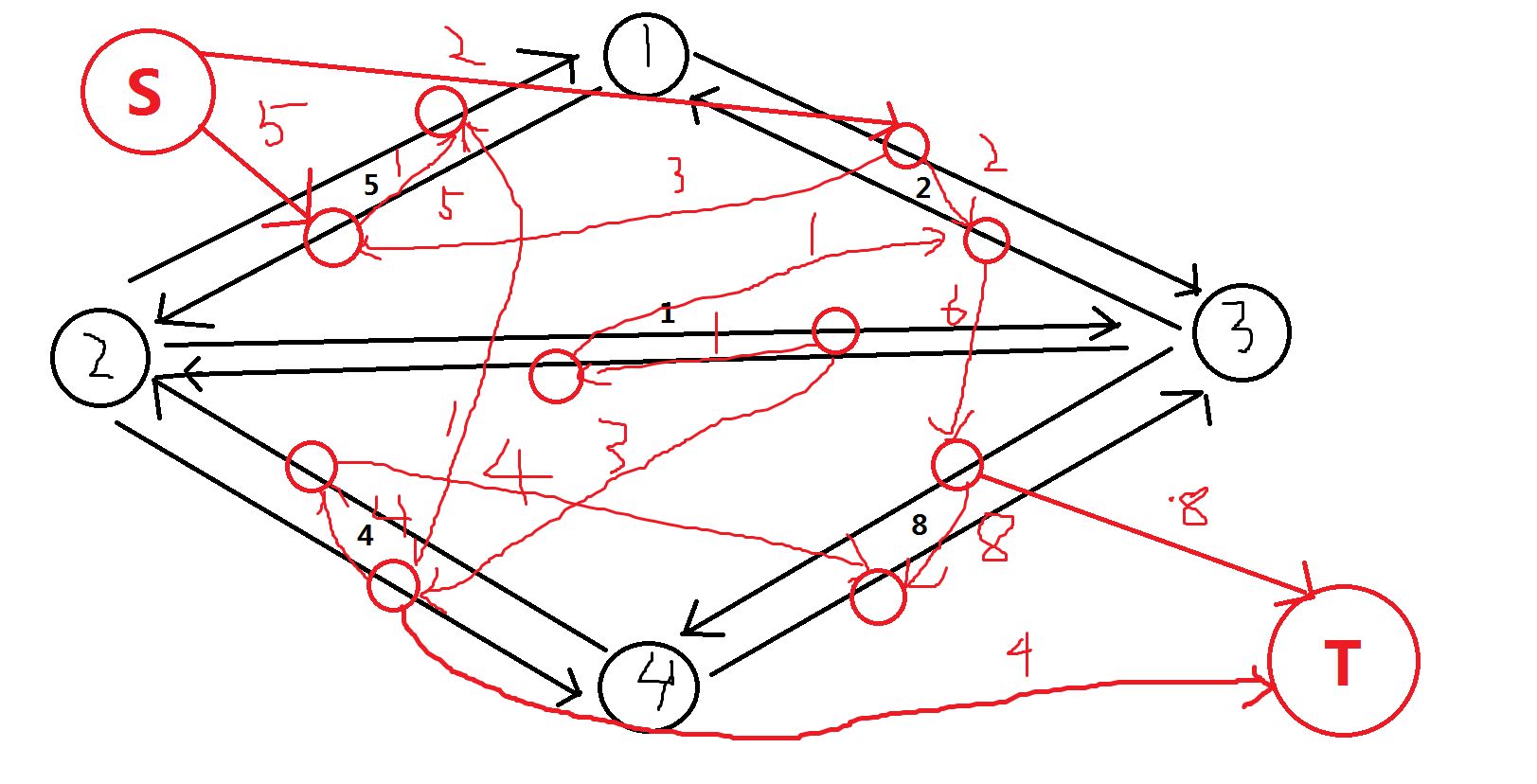
当然，最后跑一边Dijkstra，SPFA会被卡。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue> 
#include <cstdlib>
#define REP(i,k,n)  for(int i=k;i<=n;i++)
#define in(a) a=read()
#define MAXN 400040
using namespace std;
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar())
        if(ch=='-')
            f=-1;
    for(;isdigit(ch);ch=getchar())
        x=x*10+ch-'0';
    return x*f;
}
int n,m;
int S,T;
int total,head[MAXN],to[MAXN*2],nxt[MAXN*2],val[MAXN*2];
int Total,Head[2000000],To[2000000],Nxt[2000000],Val[2000000];
int vis[400010];
long long dis[400010];
struct edge{
    int id,va;
}st[MAXN*2]; 
struct node{
    int a;
    long long b;
    bool operator <(const node &x)const{
        return b>x.b;
    }
};
priority_queue<node> Q; 
inline int change(int x){
    if(x%2==1)  return x+1;
    return x-1;
} 
inline void adl(int a,int b,int c){
    total++;
    to[total]=b;
    val[total]=c;
    nxt[total]=head[a];
    head[a]=total;
    return ;
}
inline void Adl(int a,int b,int c){
    Total++;
    To[Total]=b;
    Val[Total]=c;
    Nxt[Total]=Head[a];
    Head[a]=Total;
    return ;
}
inline bool cmp(edge a,edge b){
    return a.va<b.va;
} 
inline void solve(int u){
    int cnt=0;
    for(int e=head[u];e;e=nxt[e])  st[++cnt].id=e,st[cnt].va=val[e];
    sort(st+1,st+cnt+1,cmp);//对于u的所有出边排序
    REP(i,1,cnt-1)  Adl(st[i].id,st[i+1].id,st[i+1].va-st[i].va),Adl(st[i+1].id,st[i].id,0);//连查分边
    for(int e=head[u];e;e=nxt[e])  Adl(change(e),e,val[e]);//每一条出边连向所对入边
    return ;
}
inline long long Dijkstra(){
    memset(dis,0x7f,sizeof(dis));
    dis[S]=0;
    node p;
    p.a=S,p.b=0;
    Q.push(p);
    while(!Q.empty()){
        int u=Q.top().a;Q.pop();
        if(vis[u])  continue;
        vis[u]=1;
        for(int e=Head[u];e;e=Nxt[e])
            if(dis[To[e]]>dis[u]+Val[e]){
                dis[To[e]]=dis[u]+Val[e];
                node q;
                q.a=To[e],q.b=dis[To[e]];
                Q.push(q);
            }
    }
    return dis[T];
}
int main(){
    in(n),in(m);
    int a,b,c;
    REP(i,1,m)  in(a),in(b),in(c),adl(a,b,c),adl(b,a,c);
    S=0,T=total+1;
    for(int e=head[1];e;e=nxt[e])  Adl(S,e,val[e]);//处理源点 
    for(int e=head[n];e;e=nxt[e])  Adl(change(e),T,val[e]);//处理汇点
    for(int i=1;i<=n;i++)  solve(i); 
    printf("%d",Dijkstra()); 
    return 0;
}
/*
4 5
1 2 5
1 3 2
2 3 1
2 4 4
3 4 8
*/