splay小结
splay
splay 是什么
\(Splay\)(伸展树)是一种平衡树,由 Daniel Sleator 和 Robert Endre Tarjan 在1985年发明,用于保证二叉查找树的尽量平衡 ,同时维护二叉查找树的性质,使得查找操作的时间复杂度变低。
\(Splay\) 依赖于伸展操作,而伸展操作依赖于旋转操作 。相对于其他平衡树,\(Splay\) 代码较为简单,应用范围广,实用性较强,时间复杂度还行( \(O(nlogn)\) ),不需要记录用于平衡树的冗余信息。
前置操作
前置变量
struct datay
{
int val,size,fa,lc,rc,cnt;
}a[200005];
int num,root;
\(val\) 表示当前节点的值
\(size\) 表示以该节点为树根的子树的大小
\(cnt\) 表示该值的数量
\(fa\) 表示父节点
\(lc,rc\) 表示左右儿子节点
\(num\) 表示节点个数
\(root\) 表示树根
初始化
加入两个哨兵,值分别为 \(-10^9-5\) 和 \(10^9+5\)即可
基本操作
左旋与右旋
平衡树的实现基本步骤,通过左旋与右旋将一个节点旋转到它父节点的位置,从而改变树的结构
左旋
如图
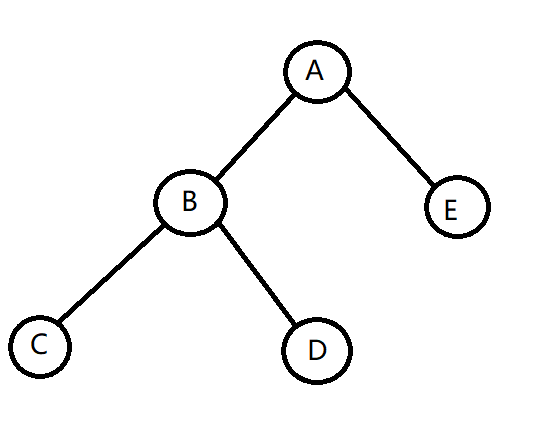
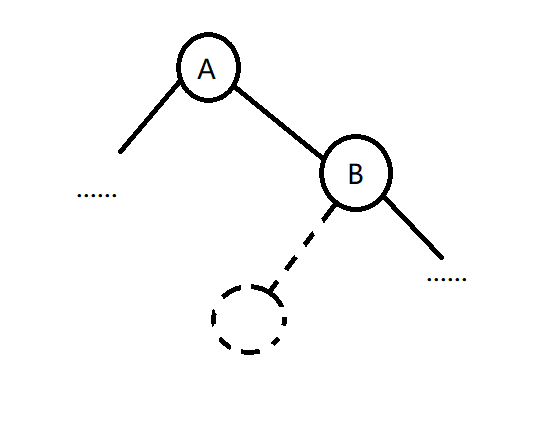
若要将 \(B\) 左旋,即会变成这样
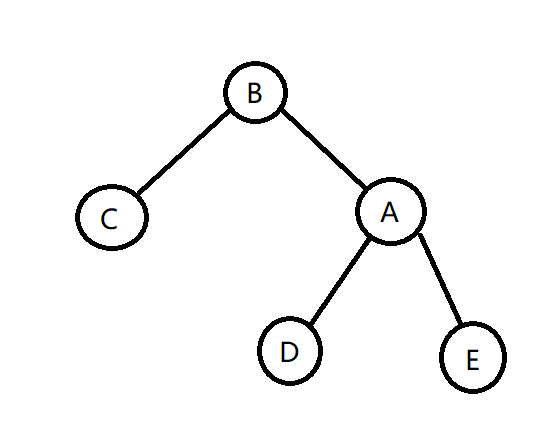
容易发现,改变了相对位置的,其实只有3个节点,分别是 \(A,B,D\) 。
就是要左旋的节点的父节点,自己与右儿子节点。
将节点 \(B\) 旋上去,他的父节点会变成它父节点的父节点,即使 \(A\) 的父节点 。
而左儿子不变,右儿子变成了原来的父节点,即是节点 \(A\) 。
\(A\) 节点右儿子不变,而父节点变成 \(B\),而因为 \(B\) 节点的原来的右节点被顶掉,左儿子变成左旋的节点的右儿子,即为 \(B\) 的右儿子 \(D\) 。
\(D\) 只用改变自己的父节点,变成原父节点的父节点,即为 \(A\)
这样一来,满足 \(BST\) 的性质,同时也将节点旋转到了更高的位置,便于后一步操作。
右旋
与左旋同理,只是左右儿子调换了而已,可以自行画图理解。
上左右旋代码:
void lturn(int x)
{
if(check(a[x].fa))a[a[a[x].fa].fa].rc=x;
else a[a[a[x].fa].fa].lc=x;
a[a[x].rc].fa=a[x].fa;
a[a[x].fa].lc=a[x].rc;
a[x].rc=a[x].fa;
a[x].fa=a[a[x].rc].fa;
a[a[x].rc].fa=x;
a[a[x].rc].size=a[a[a[x].rc].lc].size+a[a[a[x].rc].rc].size+a[a[x].rc].cnt;
a[x].size=a[a[x].lc].size+a[a[x].rc].size+a[x].cnt;
return;
}
void rturn(int x)
{
if(check(a[x].fa))a[a[a[x].fa].fa].rc=x;
else a[a[a[x].fa].fa].lc=x;
a[a[x].lc].fa=a[x].fa;
a[a[x].fa].rc=a[x].lc;
a[x].lc=a[x].fa;
a[x].fa=a[a[x].lc].fa;
a[a[x].lc].fa=x;
a[a[x].lc].size=a[a[a[x].lc].lc].size+a[a[a[x].lc].rc].size+a[a[x].lc].cnt;
a[x].size=a[a[x].lc].size+a[a[x].rc].size+a[x].cnt;
return;
}
作者打的有些麻烦,请各位大佬多加包涵
伸展splay
平衡树的实现原理,通过伸展操作将一个节点旋转到指定的节点的儿子处,来进行插入、删除等操作。
那应该如何进行 \(splay\) 呢?
对于一个节点,我们可以分类讨论:
1
父节点为左儿子,自己仍为左儿子
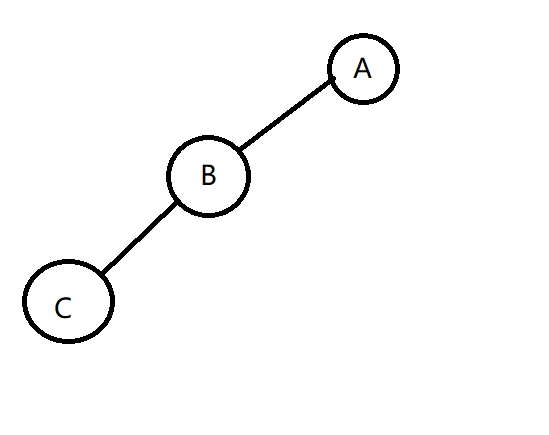
先将 \(B\) 左旋,再将 \(C\) 左旋,即可以让 \(C\) 旋转到 \(A\) 的位置。
注意,一定要先让父节点先旋,否则无法保证 \(O(nlogn)\) 的时间复杂度
2
父节点为右儿子,自己仍为右儿子
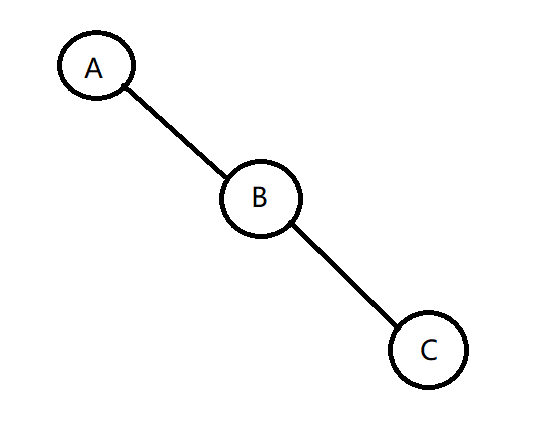
与上同理,先将父节点 \(B\) 右旋,再将 \(C\) 右旋。
3&4
父节点为左儿子,自己为右儿子 / 父节点为右儿子,自己为左儿子
只能先旋一次自己,在父节点的位置上再旋一次自己。
循环过程即使不断进行分类讨论,将自己往上旋转,直到父节点或父节点的父节点出现了目标节点,即可退出循环,若是父节点的父节点出现了目标节点,需再旋转一次,然后 \(return\) 即可
若要将一个节点旋转至根,设目标节点为 \(0\) 即可,因为只有根节点的父节点是 \(0\)。
上代码:
void splay(int x,int to)
{
bool q1,q2;
while(a[a[x].fa].fa!=to)
{
if(a[x].fa==to)
{
if(to==0)root=x;
return;
}
q1=check(a[x].fa);
q2=check(x);
//分类讨论
if(q1&&q2)rturn(a[x].fa),rturn(x);//先旋父节点
if((!q1)&&(!q2))lturn(a[x].fa),lturn(x);//先旋父节点
if(q1&&(!q2))lturn(x),rturn(x);
if((!q1)&&q2)rturn(x),lturn(x);
}
if(a[x].fa==to)return;
if(check(x))rturn(x);
else lturn(x);
if(to==0)root=x;//更新根的位置
return;
}
更多操作
前驱
定义:比自己小的且最大的那个数
从根开始往下找,碰到比查找的值大或相等的就往左,否则往右,最后递归上来时找到最靠右的,就是最后一个满足条件的那个位置作为答案
上代码:
int left(int p,int x)
{
if(p==0)return 0;
if(a[p].val<x)qw=left(a[p].rc,x),qw=qw==0?p:qw;
else qw=left(a[p].lc,x);
return qw;
}
后继
定义:比自己大的且最小的那个数
同样从根开始往下找,碰到比查找的值大的就往左,否则往右,最后递归上来找最靠左的,就是最后一个满足条件的位置。
插入
先找出插入值的前驱与后继,设为 \(A\) 与 \(B\)
将 \(A\) 旋转至根节点,将 \(B\) 旋转至 \(A\) 的儿子节点,由于 \(BST\) 的性质,\(B\) 肯定在 \(A\) 的右儿子节点。
那么,若树中已存在这个值,那么 \(B\) 的右儿子肯定是这个值所在的节点,否则为空。
因为 \(BST\) 的性质,加上 \(A,B\) 分别为原值的前驱与后继,所以两点之间肯定夹着这个值。
所以加点或修改只需要对 \(B\) 的右儿子进行操作就可以了。
若有维护 \(size\) ,记得上传。
void insert(int x)
{
int le=left(root,x),ri=right(root,x);
splay(le,0);
splay(ri,le);
if(a[ri].lc==0)
{
a[ri].lc=++num;
a[num].val=x;
a[num].size=a[num].cnt=1;
a[num].fa=ri;
a[ri].size++;
a[le].size++;
}
else a[a[ri].lc].cnt++,a[a[ri].lc].size++,a[ri].size++,a[le].size++;
total++;
return;
}
删除
与插入同理,只需反过来维护即可。
注意若是一个节点删除掉,只需要将 \(B\) 的右儿子设为空即可。
上代码:
void del(int x)
{
int le=left(root,x),ri=right(root,x);
splay(le,0);
splay(ri,le);
if(a[a[ri].lc].cnt==1)a[a[ri].lc].val=-1,a[ri].lc=0,a[le].size--,a[ri].size--;
else a[a[ri].lc].cnt--,a[a[ri].lc].size--,a[ri].size--,a[le].size--;
total--;
return;
}
查找某数的排名
从根节点往下找。
考虑做到节点 \(A\) ,希望求出这个数在以 \(A\) 为根节点的子树中的排名。
很显然,若节点 \(A\) 的权值大于这个数,往左儿子找。
否则,要往右儿子找,而返回来时,在这个子树中还未考虑的节点有 \(A\) 节点与以 \(A\) 的左儿子为根的子树中的节点。
加上他们的数量就可以了。
若此节点为空,返回0。
上代码:
int number(int p,int x)
{
if(p==0)return 0;
if(a[p].val<x)return a[p].cnt+a[a[p].lc].size+number(a[p].rc,x);
return number(a[p].lc,x);
}
查找第几小的数
仍然从根节点往下找。
考虑做到节点 \(A\),左儿子为 \(B\) ,希望求出以 \(A\) 为根节点的子树中第 \(x\) 小的数。
若左儿子的 \(size\) 大于或等于 \(x\),直接往左找。
若左儿子的 \(size\) 小于 \(x\) 且 加上自己的 \(cnt\) 后 大于等于 \(x\),直接返回这个节点。
否则,答案应在右节点,应该找的是右子树中第 \(x-B.size-A.cnt\) 的数,往右儿子递归。
最后返回答案。
上代码:
int rank(int p,int x)
{
if(a[a[p].lc].size>=x)return rank(a[p].lc,x);
if(a[p].size-a[a[p].rc].size>=x)return p;
x-=a[p].size-a[a[p].rc].size;
return rank(a[p].rc,x);
}
那现在,我们就可以A了这道题了。
Code
#include<bits/stdc++.h>
using namespace std;
struct datay
{
int val,size,fa,lc,rc,cnt;
}a[200005];
int num,root,total=0,qwee=0,poi=0;
bool check(int x)
{
if(a[a[x].fa].lc==x)return false;
return true;
}
void lturn(int x)
{
if(check(a[x].fa))a[a[a[x].fa].fa].rc=x;
else a[a[a[x].fa].fa].lc=x;
a[a[x].rc].fa=a[x].fa;
a[a[x].fa].lc=a[x].rc;
a[x].rc=a[x].fa;
a[x].fa=a[a[x].rc].fa;
a[a[x].rc].fa=x;
a[a[x].rc].size=a[a[a[x].rc].lc].size+a[a[a[x].rc].rc].size+a[a[x].rc].cnt;
a[x].size=a[a[x].lc].size+a[a[x].rc].size+a[x].cnt;
return;
}
void rturn(int x)
{
if(check(a[x].fa))a[a[a[x].fa].fa].rc=x;
else a[a[a[x].fa].fa].lc=x;
a[a[x].lc].fa=a[x].fa;
a[a[x].fa].rc=a[x].lc;
a[x].lc=a[x].fa;
a[x].fa=a[a[x].lc].fa;
a[a[x].lc].fa=x;
a[a[x].lc].size=a[a[a[x].lc].lc].size+a[a[a[x].lc].rc].size+a[a[x].lc].cnt;
a[x].size=a[a[x].lc].size+a[a[x].rc].size+a[x].cnt;
return;
}
void splay(int x,int to)
{
if(a[x].val==-1)return;
bool q1,q2;
while(a[a[x].fa].fa!=to)
{
if(a[x].fa==to)
{
if(to==0)root=x;
return;
}
q1=check(a[x].fa);
q2=check(x);
if(q1&&q2)rturn(a[x].fa),rturn(x);
if((!q1)&&(!q2))lturn(a[x].fa),lturn(x);
if(q1&&(!q2))lturn(x),rturn(x);
if((!q1)&&q2)rturn(x),lturn(x);
}
if(a[x].fa==to)return;
if(check(x))rturn(x);
else lturn(x);
if(to==0)root=x;
return;
}
int qw;
int left(int p,int x)
{
if(p==0)return 0;
if(a[p].val<x)qw=left(a[p].rc,x),qw=qw==0?p:qw;
else qw=left(a[p].lc,x);
return qw;
}
int right(int p,int x)
{
if(p==0)return 0;
if(a[p].val<=x)qw=right(a[p].rc,x);
else qw=right(a[p].lc,x),qw=qw==0?p:qw;
return qw;
}
void insert(int x)
{
int le=left(root,x),ri=right(root,x);
splay(le,0);
splay(ri,le);
if(a[ri].lc==0)
{
a[ri].lc=++num;
a[num].val=x;
a[num].size=a[num].cnt=1;
a[num].fa=ri;
a[ri].size++;
a[le].size++;
}
else a[a[ri].lc].cnt++,a[a[ri].lc].size++,a[ri].size++,a[le].size++;
total++;
return;
}
void del(int x)
{
int le=left(root,x),ri=right(root,x);
splay(le,0);
splay(ri,le);
if(a[a[ri].lc].cnt==1)a[a[ri].lc].val=-1,a[ri].lc=0,a[le].size--,a[ri].size--;
else a[a[ri].lc].cnt--,a[a[ri].lc].size--,a[ri].size--,a[le].size--;
total--;
return;
}
int rank(int p,int x)
{
if(a[a[p].lc].size>=x)return rank(a[p].lc,x);
if(a[p].size-a[a[p].rc].size>=x)return p;
x-=a[p].size-a[a[p].rc].size;
return rank(a[p].rc,x);
}
int number(int p,int x)
{
if(p==0)return 0;
if(a[p].val<x)return a[p].cnt+a[a[p].lc].size+number(a[p].rc,x);
return number(a[p].lc,x);
}
int main()
{
root=1;
num=2;
srand(time(0));
a[1].val=-1e8-5;
a[1].size=2;
a[1].rc=2;
a[1].cnt=1;
a[2].val=1e8+5;
a[2].size=1;
a[2].fa=1;
a[2].cnt=1;
total=2;
int qwe,p,x;
scanf("%d",&qwe);
for(int i=1;i<=qwe;i++)
{
scanf("%d%d",&p,&x);
if(p==1)insert(x);
else if(p==2)del(x);
else if(p==3)printf("%d\n",number(root,x));
else if(p==4)x++,printf("%d\n",a[rank(root,x)].val);
else if(p==5)printf("%d\n",a[left(root,x)].val);
else printf("%d\n",a[right(root,x)].val);
splay(rand()%num+1,0);
}
return 0;
}
更多应用:
区间翻转
实际上就是这道题。
以原序列的下标为权值,建一颗 \(splay\) 树,每个节点上记住原权值(虽然这道题权值就是下标)。
它的中序遍历即为序列。
对于一个翻转操作,我们设反转的区间为 \([l,r]\) ,那么我们可以找出平衡树中排名为 \(l-1\) 与 \(r+1\) 的数,设为 \(A,B\) ,他们分别是现序列中第 \(l-1\) 与 \(r+1\) 大的数。
那么,我们将 \(A\) 旋转至 根节点 ,将 \(B\) 节点旋转至 \(A\) 节点儿子处,这样 \(B\) 节点的左儿子及它以下的节点就是区间 \([l,r]\) 内的数。
只需要把每一个节点的左右儿子反过来就可以了。
直接该肯定会超时,我们可以对这个节点打个标记,当修改到它或查询到它时像线段树一样,将标记下推即可。
最后输出中序遍历就可以了。
Code
#include<bits/stdc++.h>
using namespace std;
struct datay
{
long long val,size,cnt,fa,lc,rc;
}a[100005];
long long n,m,num=2,root;
long long build(long long l,long long r)
{
long long mid=(l+r)>>1,q=++num;
a[q].val=mid;
a[q].size=1;
if(l==r)return q;
if(l+1<=mid)a[q].lc=build(l,mid-1);
if(mid+1<=r)a[q].rc=build(mid+1,r);
a[a[q].lc].fa=q;
a[a[q].rc].fa=q;
a[q].size=a[a[q].lc].size+a[a[q].rc].size+1;
return q;
}
bool check(long long x)
{
if(a[a[x].fa].lc==x)return 0;
return 1;
}
void lturn(int x)
{
if(check(a[x].fa))a[a[a[x].fa].fa].rc=x;
else a[a[a[x].fa].fa].lc=x;
a[a[x].rc].fa=a[x].fa;
a[a[x].fa].lc=a[x].rc;
a[x].rc=a[x].fa;
a[x].fa=a[a[x].rc].fa;
a[a[x].rc].fa=x;
a[a[x].rc].size=a[a[a[x].rc].lc].size+a[a[a[x].rc].rc].size+1;
a[x].size=a[a[x].lc].size+a[a[x].rc].size+a[x].cnt;
return;
}
void rturn(int x)
{
if(check(a[x].fa))a[a[a[x].fa].fa].rc=x;
else a[a[a[x].fa].fa].lc=x;
a[a[x].lc].fa=a[x].fa;
a[a[x].fa].rc=a[x].lc;
a[x].lc=a[x].fa;
a[x].fa=a[a[x].lc].fa;
a[a[x].lc].fa=x;
a[a[x].lc].size=a[a[a[x].lc].lc].size+a[a[a[x].lc].rc].size+1;
a[x].size=a[a[x].lc].size+a[a[x].rc].size+a[x].cnt;
return;
}
void down(long long x)
{
if(a[x].cnt==0||x==0)return;
a[a[x].lc].cnt^=1;
a[a[x].rc].cnt^=1;
swap(a[x].lc,a[x].rc);
a[x].cnt=0;
return;
}
void splay(int x,int to)
{
bool q1,q2;
while(a[a[x].fa].fa!=to)
{
if(a[x].fa==to)
{
if(to==0)root=x;
return;
}
down(a[a[x].fa].fa);
down(a[x].fa);
down(x);
q1=check(a[x].fa);
q2=check(x);
if(q1&&q2)rturn(a[x].fa),rturn(x);
if((!q1)&&(!q2))lturn(a[x].fa),lturn(x);
if(q1&&(!q2))lturn(x),rturn(x);
if((!q1)&&q2)rturn(x),lturn(x);
}
down(a[a[x].fa].fa);
down(a[x].fa);
down(x);
if(a[x].fa==to)return;
if(check(x))rturn(x);
else lturn(x);
if(to==0)root=x;
return;
}
long long rank(long long p,long long x)
{
down(p);
if(a[a[p].lc].size+1>x)return rank(a[p].lc,x);
if(a[a[p].lc].size+1==x)return p;
x-=a[a[p].lc].size+1;
return rank(a[p].rc,x);
}
void search(long long x)
{
if(x==0)return;
down(x);
search(a[x].lc);
if(abs(a[x].val)<=1e9)printf("%lld ",a[x].val);
search(a[x].rc);
return;
}
int main()
{
srand(time(0));
root=1;
a[1].val=-1e9-5;
a[1].size=2;
a[1].rc=2;
a[2].fa=1;
a[2].size=1;
a[2].val=1e9+5;
scanf("%lld%lld",&n,&m);
a[2].lc=build(1,n);
a[2].size+=n;
a[1].size+=n;
a[3].fa=2;
long long le,ri,l,r;
for(int i=1;i<=m;i++)
{
scanf("%lld%lld",&l,&r);
le=rank(root,l);
ri=rank(root,r+2);
splay(le,0);
splay(ri,le);
a[a[ri].lc].cnt^=1;
}
search(root);
return 0;
}
作者初学 \(spaly\) ,理解浅显,若有错误地方望指出,谢谢!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号