『原创』统计建模与R软件-第三章 数据描述性分析
2015-12-09 08:42 Digging4 阅读(15276) 评论(0) 收藏 举报本文由digging4发表于:http://www.cnblogs.com/digging4/p/5031203.html
统计建模与R软件-第三章
3.1某单位对100名女生测定血清总蛋白含量\((g/L)\),数据如下:
74.3 78.8 68.8 78.0 70.4 80.5 80.5 69.7 71.2 73.5
79.5 75.6 75.0 78.8 72.0 72.0 72.0 74.3 71.2 72.0
75.0 73.5 78.8 74.3 75.8 65.0 74.3 71.2 69.7 68.0
73.5 75.0 72.0 64.3 75.8 80.3 69.7 74.3 73.5 73.5
75.8 75.8 68.8 76.5 70.4 71.2 81.2 75.0 70.4 68.0
70.4 72.0 76.5 74.3 76.5 77.6 67.3 72.0 75.0 74.3
73.5 79.5 73.5 74.7 65.0 76.5 81.6 75.4 72.7 72.7
67.2 76.5 72.7 70.4 77.2 68.8 67.3 67.3 67.3 72.7
75.8 73.5 75.0 73.5 73.5 73.5 72.7 81.6 70.3 74.3
73.5 79.5 70.4 76.5 72.7 77.2 84.3 75.0 76.5 70.4
计算均值、方差、标准差、极差、标准误、变异系数、偏度、峰度。
x <- c(74.3, 78.8, 68.8, 78, 70.4, 80.5, 80.5, 69.7, 71.2, 73.5, 79.5, 75.6,
75, 78.8, 72, 72, 72, 74.3, 71.2, 72, 75, 73.5, 78.8, 74.3, 75.8, 65, 74.3,
71.2, 69.7, 68, 73.5, 75, 72, 64.3, 75.8, 80.3, 69.7, 74.3, 73.5, 73.5,
75.8, 75.8, 68.8, 76.5, 70.4, 71.2, 81.2, 75, 70.4, 68, 70.4, 72, 76.5,
74.3, 76.5, 77.6, 67.3, 72, 75, 74.3, 73.5, 79.5, 73.5, 74.7, 65, 76.5,
81.6, 75.4, 72.7, 72.7, 67.2, 76.5, 72.7, 70.4, 77.2, 68.8, 67.3, 67.3,
67.3, 72.7, 75.8, 73.5, 75, 73.5, 73.5, 73.5, 72.7, 81.6, 70.3, 74.3, 73.5,
79.5, 70.4, 76.5, 72.7, 77.2, 84.3, 75, 76.5, 70.4)
n <- length(x)
mean(x) #均值
## [1] 73.67
var(x) #方差
## [1] 15.52
sd(x) #标准差
## [1] 3.939
max(x) - min(x) #极差
## [1] 20
sd(x)/100^(1/2) # 标准误
## [1] 0.3939
100 * sd(x)/mean(x) #变异系数
## [1] 5.347
n/((n - 1) * (n - 2)) * sum(x - mean(x))^3/sd(x)^3 # 偏度
## [1] -4.411e-41
n * (n + 1)/((n - 1) * (n - 2) * (n - 3) * sd(x)^4) * sum(x - mean(x))^4 - 3 *
(n - 1)^2/(n - 2)/(n - 3) #峰度
## [1] -3.093
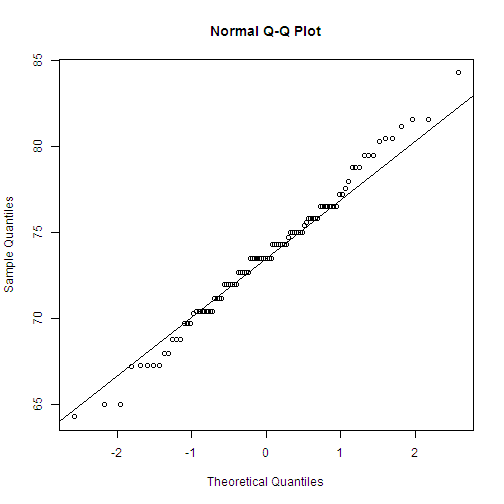
3.2 绘出习题3.1的直方图、密度估计曲线、经验分布图和qq图,并将密度估计曲线与正态密度曲线相比较,将经验分布曲线与正态分布曲线相比较(其中正态曲线的均值和标准差取习题3.1计算出的值)
# 直方图
hist(x)

# 密度估计曲线
plot(density(x), col = "blue")

# 经验分布图
plot(ecdf(x))

# qq图
qqnorm(x)
qqline(x)
# 将密度估计曲线与正态密度曲线相比较
plot(density(x), col = "blue")
x1 <- 55:154
lines(x1, dnorm(x1, mean(x), sd(x)), col = "red")

# 将经验分布曲线与正态分布曲线相比较 verticals=TRUE
# 表示画垂直线;do.p=FALSE表示数据点上不画点
plot(ecdf(x), verticals = TRUE, do.p = FALSE)
x1 <- 55:154
lines(x1, pnorm(x1, mean(x), sd(x)))

3.3 绘出习题3.1的茎叶图、箱线图,并计算五数总括。
# 茎叶图
stem(x)
##
## The decimal point is at the |
##
## 64 | 300
## 66 | 23333
## 68 | 00888777
## 70 | 344444442222
## 72 | 0000000777777555555555555
## 74 | 33333333700000004688888
## 76 | 5555555226
## 78 | 0888555
## 80 | 355266
## 82 |
## 84 | 3
# 箱线图
boxplot(x)

# 计算五数总括
fivenum(x)
## [1] 64.3 71.2 73.5 75.8 84.3
3.4 分别用W检验方法和Kolmogorov-Smirnov检验方法检验习题3.1的数据是否服从正态分布。
# 用W检验方法
# 提供w统计量和相应的p值,当p值小于某个显著性水平(比如0.05)时,则认为样本不是来自于正态分布的总体
# p-value=0.6708 大于0.05,可以认为样本是来自于正态分布的总体
shapiro.test(x)
##
## Shapiro-Wilk normality test
##
## data: x
## W = 0.9901, p-value = 0.6708
# Kolmogorov-Smirnov检验方法检验 用于比较两个分布的是否一致
# 第一个参数为待检验向量,第二个参数为用待检验向量的均值和标准差生成一个相同长度的正态分布向量
# p-value=0.6994,p值大于0.05,不能拒绝其分布一致的假设,即两个向量分布一致。
ks.test(x, rnorm(length(x), mean(x), sd(x)))
##
## Two-sample Kolmogorov-Smirnov test
##
## data: x and rnorm(length(x), mean(x), sd(x))
## D = 0.12, p-value = 0.4676
## alternative hypothesis: two-sided
3.5 小白鼠在接种了3种不同菌型的伤寒杆菌后的存活天数如表3.8所示,试绘出数据的箱线图(采用两种方法,一种是plot语句,另一种是boxplot语句)来判断小白鼠被注射三种菌型后的平均存活天数有无显著差异?
菌型 存活天数
1 2 4 3 2 4 7 7 2 2 5 4
2 5 6 8 5 10 7 12 12 6 6
3 7 11 6 6 7 9 5 5 10 6 3 10
x1 <- c(2, 4, 3, 2, 4, 7, 7, 2, 2, 5, 4)
x2 <- c(5, 6, 8, 5, 10, 7, 12, 12, 6, 6)
x3 <- c(7, 11, 6, 6, 7, 9, 5, 5, 10, 6, 3, 10)
#
# 从箱线图中可以看到,菌型2和3的平均存活天数无显著差异,但是与菌型1的有显著差异
boxplot(x1, x2, x3)

# 用plot画箱线图
x <- c(x1, x2, x3)
f <- factor(c(rep(1, 11), rep(2, 10), rep(3, 12)))
plot(f, x)

3.6 绘出例3.16关于三项指标的离散图,从图中分析例3.16的结论的合理性。
# 3.16的结论是x1、x2和x3两两均不相关 从散点图看出,三个属性两两均不相关
df <- data.frame(硬度 = c(65, 70, 70, 69, 66, 67, 68, 72, 66, 68), 变形 = c(45,
45, 48, 46, 50, 46, 47, 43, 47, 48), 弹性 = c(27.6, 30.7, 31.8, 32.6, 31,
31.3, 37, 33.6, 33.1, 34.2))
pairs(df)

3.7 某校测得19名学生的四项指标,性别、年龄、身高(cm)和 体重(磅),具体数据由表3.9所示,
(1)试绘出体重对于身高的散点图,
(2)绘出不同性别情况下,体重与身高的散点图
(3)绘出不同年龄段的体重和身高的散点图
(4)分不同性别和不同年龄段的体重与身高的散点图
学号 姓名 性别 年龄 身高 体重
01 Alice F 13 56.5 84.0
02 Becka F 13 65.3 98.0
03 Gail F 14 64.3 90.0
04 Karen F 12 56.3 77.0
05 Kathy F 12 59.8 84.5
06 Mary F 15 66.5 112.0
07 Sandy F 11 51.3 50.5
08 Sharon F 15 62.5 112.5
09 Tammy F 14 62.8 102.5
10 Alfred M 14 69.0 112.5
11 Duke M 14 63.5 102.5
12 Guido M 15 67.0 133.0
13 James M 12 57.3 83.0
14 Jeffrey M 13 62.5 84.0
15 John M 12 59.0 99.5
16 Philip M 16 72.0 150.0
17 Robert M 12 64.8 128.0
18 Thomas M 11 57.5 85.0
19 William M 15 66.5 112.0
df <- data.frame(no = c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19), name = c("Alice", "Becka", "Gail", "Karen", "Kathy", "Mary",
"Sandy", "Sharon", "Tammy", "Alfred", "Duke", "Guido", "James", "Jeffrey",
"John", "Philip", "Robert", "Thomas", "William"), sex = c("F", "F", "F",
"F", "F", "F", "F", "F", "F", "M", "M", "M", "M", "M", "M", "M", "M", "M",
"M"), age = c(13, 13, 14, 12, 12, 15, 11, 15, 14, 14, 14, 15, 12, 13, 12,
16, 12, 11, 15), high = c(56.5, 65.3, 64.3, 56.3, 59.8, 66.5, 51.3, 62.5,
62.8, 69, 63.5, 67, 57.3, 62.5, 59, 72, 64.8, 57.5, 66.5), weight = c(84,
98, 90, 77, 84.5, 112, 50.5, 112.5, 102.5, 112.5, 102.5, 133, 83, 84, 99.5,
150, 128, 85, 112))
# 试绘出体重对于身高的散点图
plot(df$high, df$weight)

# 绘出不同性别情况下,体重与身高的散点图
coplot(df$high ~ df$weight | df$sex)

# 绘出不同年龄段的体重和身高的散点图
coplot(df$high ~ df$weight | df$age)

# 分不同性别和不同年龄段的体重与身高的散点图
coplot(df$high ~ df$weight | df$sex + df$age)

3.8 画出函数\(z=x^4-2x^2y+x^2-2xy+2y^2+\frac{9}{2}x-4y+4\) 在区间\(-2\leqslant x \leqslant 3, -1\leqslant y\leqslant 7\)上的三维网格曲面和二维等值线,其中\(x\)与\(y\)各点之间的间隔为0.05,等值线的值分别为0, 1, 2, 3, 4, 5, 10, 15, 20, 30, 40, 50, 60, 80, 100,共15条,(注,在三维图形中选择合适的角度)
# 画二维等值线
x <- seq(-2, 3, 0.05)
y <- seq(-1, 7, 0.05)
f <- outer(x, y, function(x, y) x^4 - 2 * x^2 * y + x^2 - 2 * x * y + 2 * y^2 +
9/2 * x - 4 * y + 4)
contour(x, y, f, levels = c(0, 1, 2, 3, 4, 5, 10, 15, 20, 30, 40, 50, 60, 80,
100))

# 画三维网格曲面
persp(x, y, f, theta = 90, phi = 25, expand = 0.5)

3.9 用\(pearson\)相关检验发检验习题3.7中的身高与体重是否相关
# 第一二为两个长度相等的向量,p值小于0.05时拒绝原假设,认为两个向量相关
cor.test(df$high, df$weight, method = "pearson")
##
## Pearson's product-moment correlation
##
## data: df$high and df$weight
## t = 7.555, df = 17, p-value = 7.887e-07
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.7044 0.9523
## sample estimates:
## cor
## 0.8778
3.10 绘出例3.17中48名求职者数据的星图
(1)以15项自变量FL,APP,... SUIT为星图的轴
(2)以\(G_1,G_2, \cdots,G_5\)为星图的轴,通过这些星图,你能否说明应选哪6名应聘者。
为使星图能够充分反映应聘者的情况,在作图中可适当调整各种参数。
rt <- data.frame(ID = c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48), FL = c(6, 9, 7,
5, 6, 7, 9, 9, 9, 4, 4, 4, 6, 8, 4, 6, 8, 6, 6, 4, 3, 9, 7, 9, 6, 7, 2,
6, 4, 4, 5, 3, 2, 3, 6, 9, 4, 4, 10, 10, 10, 10, 3, 7, 9, 9, 0, 0), APP = c(7,
10, 8, 6, 8, 7, 9, 9, 9, 7, 7, 7, 9, 9, 8, 9, 7, 8, 7, 8, 8, 8, 10, 8, 9,
8, 10, 3, 3, 6, 5, 3, 3, 4, 7, 8, 9, 9, 6, 6, 7, 3, 4, 7, 6, 8, 7, 6), AA = c(2,
5, 3, 8, 8, 7, 8, 9, 7, 10, 10, 10, 8, 8, 8, 6, 7, 8, 8, 7, 6, 7, 7, 7,
7, 7, 7, 5, 4, 5, 4, 5, 5, 6, 4, 5, 6, 6, 9, 9, 8, 8, 9, 7, 10, 10, 10,
10), LA = c(5, 8, 6, 5, 8, 6, 8, 8, 8, 2, 0, 4, 10, 9, 7, 7, 7, 4, 4, 8,
8, 8, 9, 10, 7, 8, 9, 3, 3, 6, 7, 7, 7, 4, 3, 5, 4, 6, 10, 10, 0, 0, 8,
6, 9, 10, 3, 1), SC = c(8, 10, 9, 6, 4, 8, 8, 9, 8, 10, 10, 10, 5, 6, 5,
8, 9, 8, 7, 8, 8, 9, 9, 8, 4, 5, 8, 5, 3, 9, 8, 7, 7, 3, 3, 6, 10, 9, 9,
9, 2, 1, 2, 9, 7, 7, 5, 5), LC = c(7, 9, 8, 5, 4, 7, 8, 9, 8, 10, 8, 10,
4, 3, 4, 9, 5, 8, 8, 9, 8, 10, 9, 10, 5, 4, 9, 3, 0, 4, 4, 9, 9, 3, 0, 6,
8, 9, 10, 10, 1, 1, 4, 8, 7, 9, 0, 0), HON = c(8, 9, 9, 9, 9, 10, 8, 8,
8, 7, 3, 7, 9, 8, 10, 8, 8, 6, 5, 10, 10, 10, 10, 10, 9, 8, 10, 5, 0, 10,
10, 10, 10, 8, 9, 8, 8, 7, 10, 10, 2, 0, 5, 8, 10, 10, 10, 10), SMS = c(8,
10, 7, 2, 5, 5, 8, 8, 5, 10, 9, 8, 4, 2, 2, 9, 6, 4, 4, 5, 5, 10, 10, 10,
3, 2, 5, 0, 0, 3, 3, 3, 3, 1, 0, 2, 9, 9, 10, 10, 0, 0, 3, 6, 2, 3, 0, 0),
EXP = c(3, 5, 4, 8, 8, 9, 10, 10, 9, 3, 5, 2, 4, 5, 7, 8, 6, 3, 4, 2, 3,
3, 3, 2, 2, 3, 3, 0, 0, 1, 2, 2, 2, 1, 1, 2, 1, 1, 10, 10, 10, 10, 6,
8, 1, 1, 0, 0), DRV = c(8, 9, 9, 4, 5, 6, 8, 9, 8, 10, 9, 8, 4, 2, 5,
8, 7, 3, 2, 6, 6, 10, 9, 9, 4, 4, 5, 3, 4, 3, 5, 5, 2, 3, 0, 2, 3, 2,
10, 10, 2, 0, 2, 8, 5, 5, 2, 2), AMB = c(9, 9, 9, 5, 5, 5, 10, 10, 9,
10, 10, 8, 5, 6, 3, 7, 8, 6, 6, 7, 7, 8, 9, 7, 4, 5, 6, 3, 4, 3, 5,
3, 3, 3, 2, 4, 9, 10, 8, 10, 0, 0, 1, 10, 5, 7, 2, 2), GSP = c(7, 8,
8, 8, 8, 8, 8, 9, 8, 10, 8, 10, 4, 6, 6, 6, 6, 7, 8, 9, 8, 10, 10, 9,
4, 6, 7, 0, 0, 2, 3, 7, 6, 3, 3, 5, 7, 8, 10, 10, 3, 0, 3, 8, 7, 9,
0, 0), POT = c(5, 8, 6, 7, 8, 6, 9, 9, 8, 9, 10, 10, 7, 7, 6, 8, 6,
2, 3, 8, 8, 8, 9, 9, 4, 5, 6, 0, 0, 2, 4, 5, 4, 2, 1, 6, 5, 5, 10, 10,
0, 0, 3, 8, 8, 9, 0, 0), KJ = c(7, 8, 8, 6, 7, 6, 8, 9, 8, 3, 2, 3,
6, 5, 4, 6, 7, 6, 5, 8, 5, 10, 10, 10, 5, 5, 4, 5, 5, 7, 8, 5, 5, 5,
5, 6, 3, 5, 10, 10, 0, 0, 3, 6, 4, 4, 0, 0), SUIT = c(10, 10, 10, 5,
7, 6, 10, 10, 10, 10, 5, 7, 8, 6, 6, 10, 8, 4, 4, 9, 8, 8, 8, 8, 4,
6, 5, 0, 0, 3, 3, 2, 2, 2, 3, 3, 2, 2, 10, 10, 10, 10, 8, 5, 5, 4, 0,
0))
# 以15项自变量FL,APP,... SUIT为星图的轴
stars(rt[, -1]) #把id列去掉

#
# 以$G_1,G_2,\cdots,G_5$为星图的轴,通过这些星图,你能否说明应选哪6名应聘者。
rt2 <- data.frame(G1 = (rt$SC + rt$LC + rt$SMS + rt$DRV + rt$AMB + rt$GSP +
rt$POT)/7, G2 = (rt$FL + rt$EXP + rt$SUIT)/3, G3 = (rt$LA + rt$HON + rt$KJ)/3,
G4 = rt$AA, G5 = rt$APP)
stars(rt2)

3.11 绘出例3.17中48名求职者数据的调和曲线,以\(G_1,G_2, \cdots,G_5\)为自变量。
#
# 可以画调和曲线的包有两个,一个是谢老大编的MSG包,里面的andrews.curve()可以很轻松的画出来,目前依然可用,另一个是Jaroslav
# Myslivec专门为调和曲线写的andrews包,里面的andrews()函数可以画,画调和曲线这两个足够用了
unison <- function(x) {
# x is a matrix or data frame of data
if (is.data.frame(x) == TRUE)
x <- as.matrix(x)
t <- seq(-pi, pi, pi/30)
m <- nrow(x)
n <- ncol(x)
f <- array(0, c(m, length(t)))
for (i in 1:m) {
f[i, ] <- x[i, 1]/sqrt(2)
for (j in 2:n) {
if (j%%2 == 0)
f[i, ] <- f[i, ] + x[i, j] * sin(j/2 * t) else f[i, ] <- f[i, ] + x[i, j] * cos(j%/%2 * t)
}
}
plot(c(-pi, pi), c(min(f), max(f)), type = "n", main = "The Unison graph of Data",
xlab = "t", ylab = "f(t)")
for (i in 1:m) lines(t, f[i, ], col = i)
}
unison(rt2)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号