快速排序

快速排序是冒泡排序的改进版，也是最好的一种内排序，在很多面试题中都会出现，也是作为程序员必须掌握的一种排序方法。

【思想】

1.在待排序的元素任取一个元素作为基准(通常选第一个元素，但最的选择方法是从待排序元素中随机选取一个作为基准)，称为基准元素；
2.将待排序的元素进行分区，比基准元素大的元素放在它的右边，比其小的放在它的左边；
3.对左右两个分区重复以上步骤直到所有元素都是有序的。
你可以把快速排序联想成东拆西补或西拆东补，一边拆一边补，直到所有元素达到有序状态。
图解如下：

 

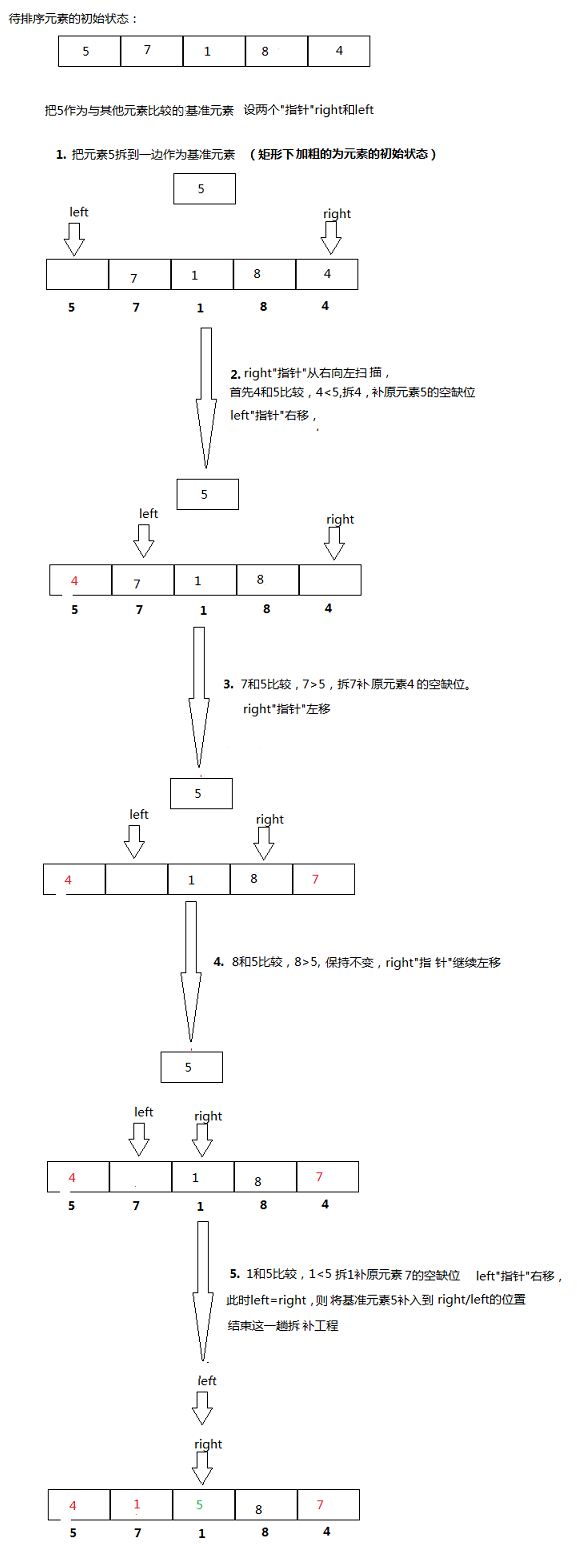
6.对元素5两边的元素也重复以上操作，直到元素达到有序状态。

很明显代码用递归写更方便。

我用数组来模拟快速排序。

【写法一】

#include<iostream>   
using namespace std;
int a[10];
void fastSorting(int left, int right)
{
    int x = a[left], l = left, r = right;//以第一个数为参照做比较   
    if (l >= r)return;
    while (l<r)
    {
        while (l<r&&a[r] >= x)   //x=a[s]
            r--; //不小于分界值的留在右边，遇到小于的停止   
        a[l] = a[r];
        while (l<r&&a[l] <= x)
            l++; //小于分界值的留在左边，遇到不小于的停止   
        a[r] = a[l];
    }
    a[r] = x;
    fastSorting(left, r - 1);
    fastSorting(r + 1, right);//递归   
}

int main()
{
    int i;
    for (i = 0; i<10; i++)
        a[i] = 10 - i; //输入数组元素   
    fastSorting(0, 9); //执行排序函数   
    for (i = 0; i<10; i++) //输出排序后结果   
        cout << a[i] << " ";
    cout << endl;
    system("pause");
} 

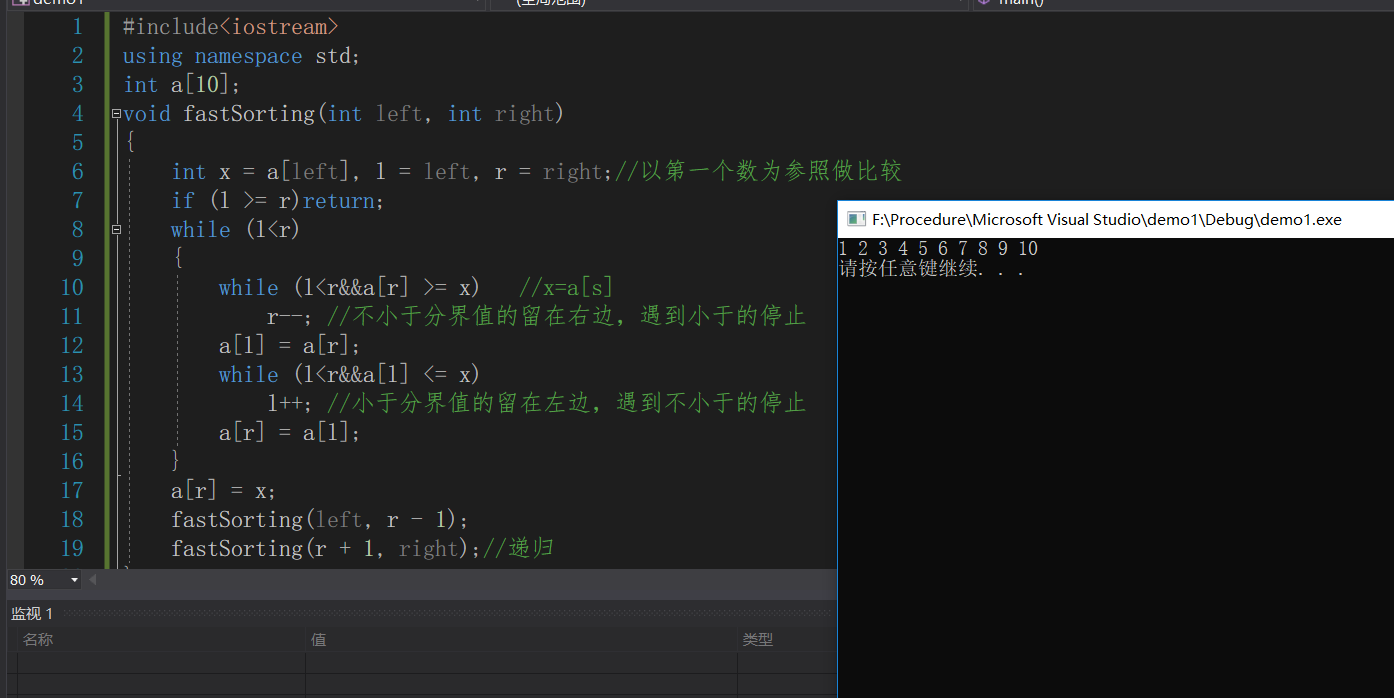
效果如上图所示。

 【写法二】

#include<iostream>
#include<iomanip>
using namespace std;

//一趟排序过程
int Partition(int *arr, int low, int high)
{//对数组arr中的arr[low...hight]进行一趟排序，返回枢轴位置
    int pivotkey= arr[low];                          //用子表的第一个记录做枢轴记录，枢轴记录关键字保存在pivotkey中
    while(low < high)                                //从表的两端交替的向中间扫描
    {
        while(low < high && arr[high] >=  pivotkey)
            --high;
            arr[low] = arr[high];                    //比枢轴记录小的记录移动到低端

        while(low < high && arr[low] <=  pivotkey)
            ++low;
        arr[high] = arr[low];                      //比枢轴记录大的记录移动到高端
        
    } //while
    arr[low] = pivotkey;//arr[0]                  //枢轴记录到位

    return low;                                    //返回枢轴位置
} 

//递归调用
void QSort(int *arr, int low, int high)
{
    if(low < high)                             //长度大于1
    {
        int pivotloc = Partition(arr,low,high); //将arr[low..... high]一分为二，pivotloc是枢轴位置
        QSort(arr,low,pivotloc-1);              //对左字标递归排序
        QSort(arr,pivotloc+1,high);              //对右字标递归排序
    }
}

//对数组做快速排序
void QuickSort(int *arr, int n)
{
        
    QSort(arr,0,n-1);//n为数组中值的个数 所以最后一个下标为n-1
}


int main()
{
    int a[100];
    for(int i = 0; i < 10; i++)
        a[i] = 10-i;
    
    QuickSort(a,10);
    for(int j = 0; j < 10; j++)
        cout<<a[j]<<ends;
    cout<<endl;

    return 0;
}

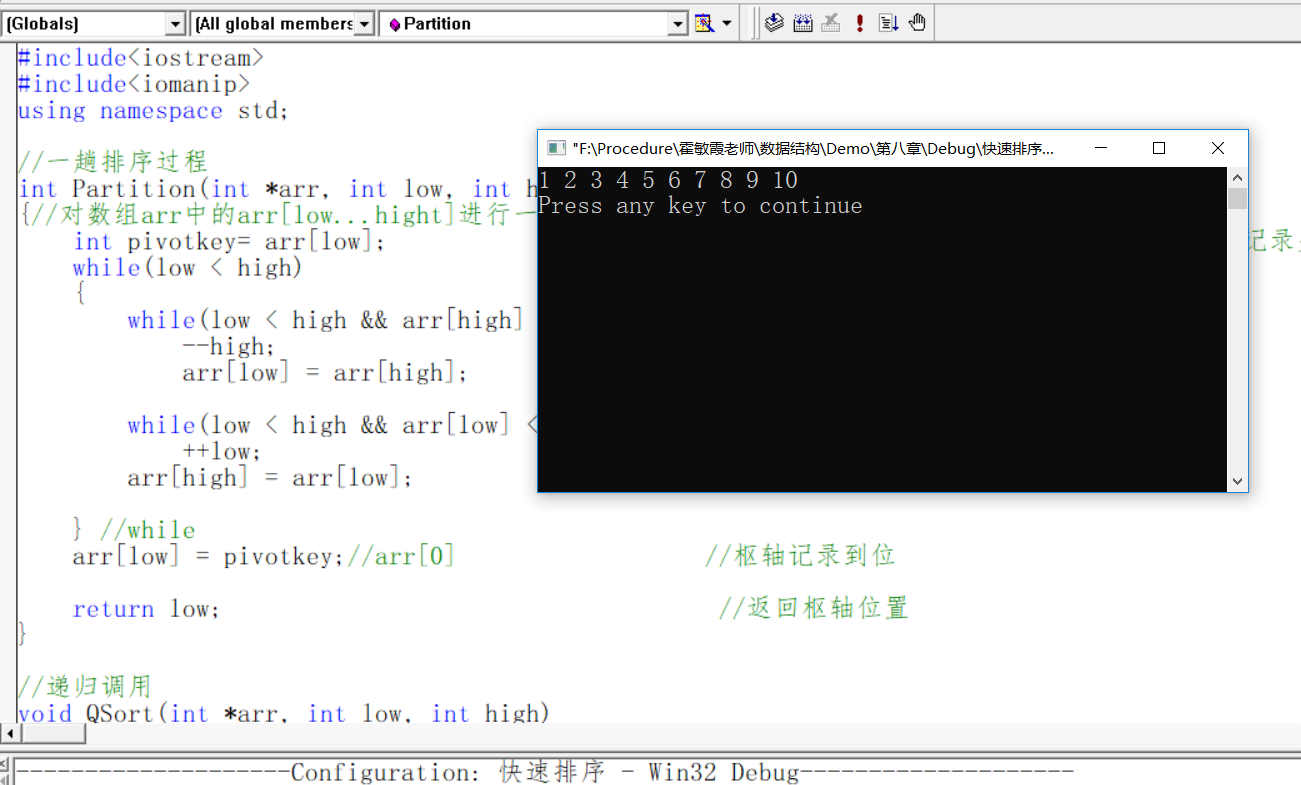
效果如上图所示。

 

算法分析：1.当分区选取的基准元素为待排序元素中的最大或最小值时，为最坏的情况，时间复杂度和直接插入排序的一样，移动次数达到最大值
Cmax = 1+2+...+(n-1) = n*(n-1)/2 = O(n2) 此时最好时间复杂为O(n2)
2.当分区选取的基准元素为待排序元素中的"中值"，为最好的情况，时间复杂度为O(nlog2n)。
3.快速排序的空间复杂度为O(log2n).
4.当待排序元素类似[6,1,3,7,3]且基准元素为6时，经过分区，形成[1,3,3,6,7],两个3的相对位置发生了改变，所是快速排序是一种不稳定排序。