二叉树
一、定义一个二叉树节点。
一个二叉数节点包含数据域、指向二叉树左右孩子的指针。
1 typedef struct BiTNode 2 { 3 ElemType data;//结点数据 4 struct BiTNode *lchild, *rchild;//指向左右孩子的指针 5 }BiTNode, *BiTree;
二、二叉树的遍历。
递归遍历实现。
1、先序遍历。
先序遍历二叉树的操作定义如下:
若二叉树为空,则空操作;否则
(1)访问根节点。
(2)先序遍历左子树。
(3)先序遍历右子树。
1 //前序遍历二叉树(递归) 2 void preOrderTraverse(BiTree T, int level) 3 { 4 if(T)//二叉树非空 5 { 6 visit(T->data, level+1);//访问根节点 7 preOrderTraverse(T->lchild, level+1);//先序遍历左指数 8 preOrderTraverse(T->rchild, level+1);//先序遍历右指数 9 } 10 }
2、中序遍历。
中序遍历二叉树的操作定义如下:
若二叉树为空,则空操作;否则
(1)中序遍历左子树。
(2)访问根节点。
(3)中序遍历右子树。
1 //中序遍历二叉树(递归) 2 void InOrderTraverse(BiTree T, int level) 3 { 4 if(T)//二叉树非空 5 { 6 7 InOrderTraverse(T->lchild, level+1);//中序遍历左指数 8 visit(T->data, level+1);//访问根节点 9 InOrderTraverse(T->rchild, level+1);//中序遍历右指数 10 } 11 }
3、后序遍历。
若二叉树为空,则空操作;否则
(1)后序遍历左子树。
(2)后序遍历右子树。
(3)访问根节点。
1 //后序遍历二叉树(递归) 2 void PostOrderTraverse(BiTree T, int level) 3 { 4 if(T)//二叉树非空 5 { 6 7 PostOrderTraverse(T->lchild, level+1);//后序遍历左指数 8 PostOrderTraverse(T->rchild, level+1);//后序遍历右指数 9 visit(T->data, level+1);//访问根节点 10 } 11 12 }
非递归遍历实现。
层次遍历二叉树。
层次遍历二叉树要用到队列来实现,我这里用c++中的STL中的queue容器来实现。(记得头文件#include<queue>)
1 //层次遍历二叉树 2 void LevelOrderTraverse(BiTree T) 3 { 4 queue<BiTree > s;//定义一个队列 5 BiTree p;//节点指针 6 BiTree q; 7 8 p = T; 9 if(p == NULL)//树空返回函数结束 10 { 11 printf("tree is empty!!"); 12 return ; 13 } 14 15 s.push(p);//将根节点入队 16 while(!s.empty()) 17 { 18 p = s.front();//出队 19 s.pop(); 20 21 if(NULL != p->lchild)//如果左节点不为空 左节点入队 22 { 23 q = p->lchild; 24 s.push(q); 25 26 } 27 if(NULL != p->rchild)//如果右节点不为空 右节点入队 28 { 29 q = p->rchild; 30 s.push(q); 31 32 } 33 cout<<p->data<<ends; 34 35 } 36 37 38 }
前序遍历。
前序遍历二叉树要用到栈来实现,我这里用c++中的STL中的stack容器来实现。(记得头文件#include<stack>)
【算法步骤】
(1)初始化一个空栈S,指针p指向根节点。
(2)当p非空或者栈S非空,循环执行以操作:
●如果p非空,输出(根)节点,将p进栈,p指向该节点的左孩子。
●如果p为空,这弹出栈顶元素,将p指向该结点的右孩子。
1 void preOrderTraverse(BiTree T) //非递归前序遍历 2 { 3 stack<BiTree> s; //申请一个存储二叉树指针的栈 4 BiTree p=T; //指向二叉树的指针 指向树的根节点 5 while(p!=NULL||!s.empty())//当指针不为空 或者栈不为空 6 { 7 while(p!=NULL)//指针不为空循环 指针指向最左端的一个节点 8 { 9 cout<<p->data<<" ";//输出根节点 10 s.push(p);//节点存入栈中 11 p=p->lchild;//p指向左孩子 12 } 13 if(!s.empty())//当栈不为空 14 { 15 p=s.top();//栈顶元素赋值给p 16 s.pop();//弹栈 17 p=p->rchild;//p指向右孩子 18 } 19 } 20 }
中序遍历。
非递归中序遍历二叉树也要用到栈来实现,我这里用c++中的STL中的stack容器来实现。
【算法步骤】
(1)初始化一个空栈S,指针p指向根节点。
(2)当p非空或者栈S非空,循环执行以操作:
●如果p非空,则将p进栈,p指向该节点的左孩子。
●如果p为空,这弹出栈顶元素并访问,将p指向该结点的右孩子。
1 void InOrderTraverse(BiTree T) //非递归中序遍历 2 { 3 stack<BiTree> s; 4 BiTree p = T; 5 while(p!=NULL||!s.empty()) 6 { 7 while(p!=NULL) 8 { 9 s.push(p); 10 p=p->lchild; 11 } 12 if(!s.empty()) 13 { 14 p=s.top(); 15 cout<<p->data<<" "; 16 s.pop(); 17 p=p->rchild; 18 } 19 } 20 }
总代码:
1 #include<iostream> 2 #include<stack>//栈的头文件 3 #include<queue>//队列的头文件 4 typedef char ElemType; 5 using namespace std; 6 7 //二叉树节点的定义 8 typedef struct BiTNode 9 { 10 ElemType data;//结点数据 11 struct BiTNode *lchild, *rchild;//指向左右孩子的指针 12 }BiTNode, *BiTree; 13 14 15 //创建一颗二叉树,y约定用户遵照前序遍历的方式输入数据 16 void CreatBiTree(BiTree &T) 17 { 18 char c; 19 cin>>c; 20 if( '#' == c ) 21 { 22 T = NULL; 23 } 24 else 25 { 26 T = new BiTNode; 27 T->data = c; 28 CreatBiTree(T->lchild);//创建一个左指数 29 CreatBiTree(T->rchild);//创建一个右指数 30 } 31 } 32 33 34 //访问二叉树的具体节点的具体操作 35 void visit(char c,int level) 36 { 37 printf("%c 位于第 %d 层\n" ,c,level); 38 } 39 40 41 42 //前序遍历二叉树(递归) 43 void preOrderTraverse(BiTree T, int level) 44 { 45 if(T)//二叉树非空 46 { 47 visit(T->data, level+1);//访问根节点 48 preOrderTraverse(T->lchild, level+1);//先序遍历左指数 49 preOrderTraverse(T->rchild, level+1);//先序遍历右指数 50 } 51 } 52 53 //中序遍历二叉树(递归) 54 void InOrderTraverse(BiTree T, int level) 55 { 56 if(T)//二叉树非空 57 { 58 59 InOrderTraverse(T->lchild, level+1);//中序遍历左指数 60 visit(T->data, level+1);//访问根节点(我这里写了一个输出函数也可以直接输出) 61 InOrderTraverse(T->rchild, level+1);//中序遍历右指数 62 } 63 } 64 65 //后序遍历二叉树(递归) 66 void PostOrderTraverse(BiTree T, int level) 67 { 68 if(T)//二叉树非空 69 { 70 71 PostOrderTraverse(T->lchild, level+1);//后序遍历左指数 72 PostOrderTraverse(T->rchild, level+1);//后序遍历右指数 73 visit(T->data, level+1);//访问根节点 74 } 75 76 } 77 78 //层次遍历二叉树 79 void LevelOrderTraverse(BiTree T) 80 { 81 queue<BiTree > s;//定义一个队列 82 BiTree p;//节点指针 83 BiTree q; 84 85 p = T; 86 if(p == NULL)//树空返回函数结束 87 { 88 printf("tree is empty!!"); 89 return ; 90 } 91 92 s.push(p);//将根节点入队 93 while(!s.empty()) 94 { 95 p = s.front();//出队 96 s.pop(); 97 98 if(NULL != p->lchild)//如果左节点不为空 左节点入队 99 { 100 q = p->lchild; 101 s.push(q); 102 103 } 104 if(NULL != p->rchild)//如果右节点不为空 右节点入队 105 { 106 q = p->rchild; 107 s.push(q); 108 109 } 110 cout<<p->data<<ends; 111 112 } 113 114 115 } 116 117 void preOrderTraverse(BiTree T) //非递归前序遍历 118 { 119 stack<BiTree> s; //申请一个存储二叉树指针的栈 120 BiTree p=T; //指向二叉树的指针 指向树的根节点 121 while(p!=NULL||!s.empty())//当指针不为空 或者栈不为空 122 { 123 while(p!=NULL)//指针不为空循环 指针指向最左端的一个节点 124 { 125 cout<<p->data<<" ";//输出根节点 126 s.push(p);//节点存入栈中 127 p=p->lchild;//p指向左孩子 128 } 129 if(!s.empty())//当栈不为空 130 { 131 p=s.top();//栈顶元素赋值给p 132 s.pop();//弹栈 133 p=p->rchild;//p指向右孩子 134 } 135 } 136 } 137 138 void InOrderTraverse(BiTree T) //非递归中序遍历 139 { 140 stack<BiTree> s; 141 BiTree p = T; 142 while(p!=NULL||!s.empty()) 143 { 144 while(p!=NULL) 145 { 146 s.push(p); 147 p=p->lchild; 148 } 149 if(!s.empty()) 150 { 151 p=s.top(); 152 cout<<p->data<<" "; 153 s.pop(); 154 p=p->rchild; 155 } 156 } 157 } 158 159 160 161 162 void main() 163 { 164 165 //ABDH##I##E#J##CF#K##G###// 166 BiTree tree;//创建一个二叉树指针 167 cout<<"请输入建立二叉链表的序列:\n"; 168 CreatBiTree(tree); 169 170 cout<<endl<<"前序遍历的结果为(递归):\n"; 171 preOrderTraverse(tree,1); 172 cout<<"前序遍历的结果为(非递归):\n"; 173 preOrderTraverse(tree); 174 175 cout<<"中序遍历的结果为(递归):\n"; 176 InOrderTraverse(tree,1); 177 cout<<"中序遍历的结果为(非递归):\n"; 178 InOrderTraverse(tree); 179 180 181 cout<<endl<<"后序遍历的结果为(递归):\n"; 182 PostOrderTraverse(tree,1); 183 184 cout<<endl<<"层次遍历的结果为:\n"; 185 LevelOrderTraverse(tree); 186 187 188 189 190 cout<<endl; 191 }
注:在递归遍历中我写了一个输出函数(visit),你可以不用写直接输出结点(记得把递归遍历中的第二个参数level删除)。
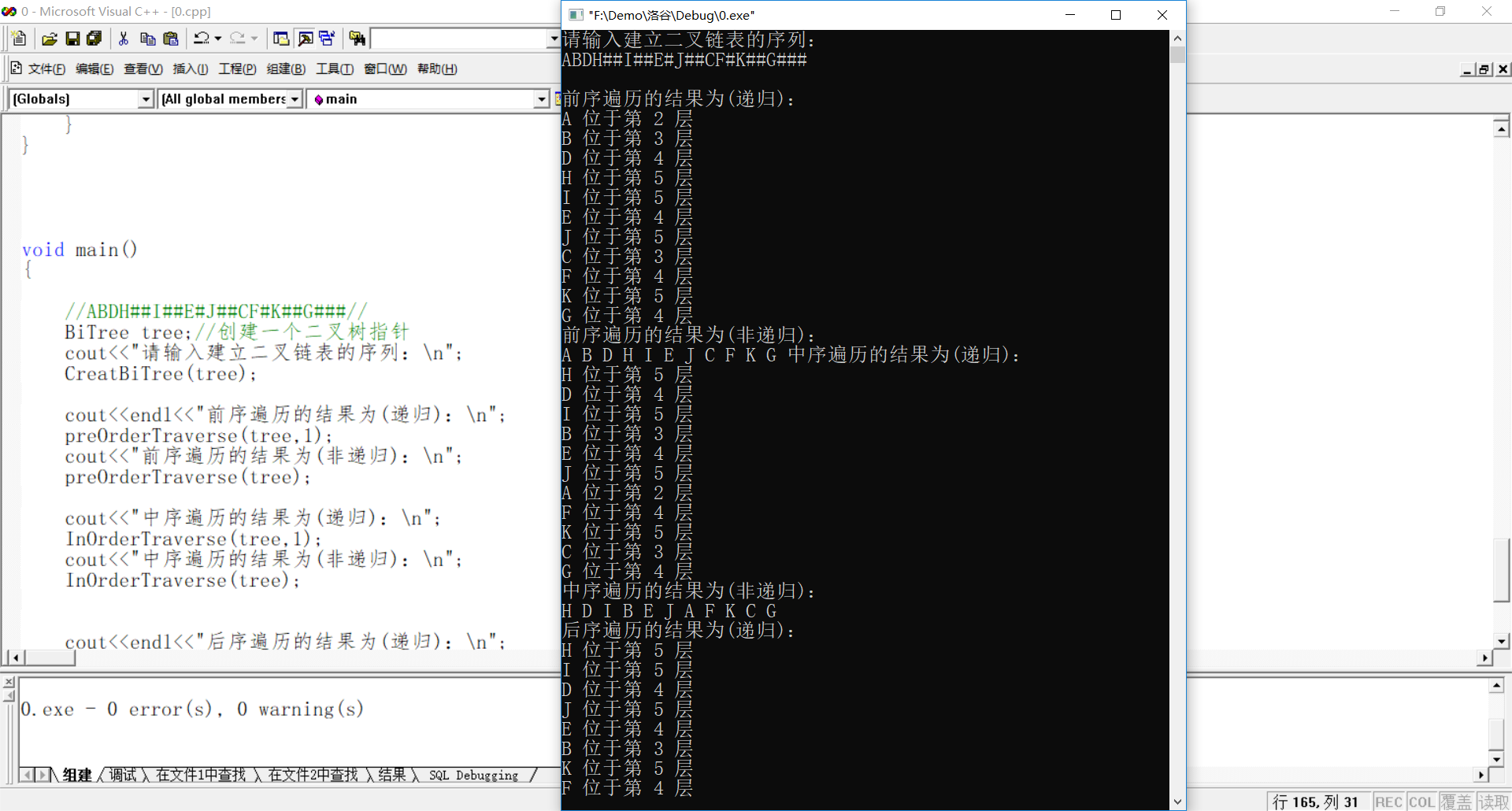
【效果如下】


